3.4.1 圆周角和圆心角的关系(第1课时) 课件(共23张PPT)
文档属性
| 名称 | 3.4.1 圆周角和圆心角的关系(第1课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 16:36:54 | ||
图片预览





文档简介
(共23张PPT)
第三章 圆
北师大版九年级数学下册
4.1 圆周角和圆心角的关系
学习&目标
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的关系”.(难点)
情境&导入
1.圆心角的定义
顶点在圆心的角叫圆心角.
2.圆心角的度数和它所对的弧的度数有何关系
如图:∠AOB 弧AB的度数
=
3.在同圆或等圆中,如果两个圆心角、两条___、两条___中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧
弦
情境&导入
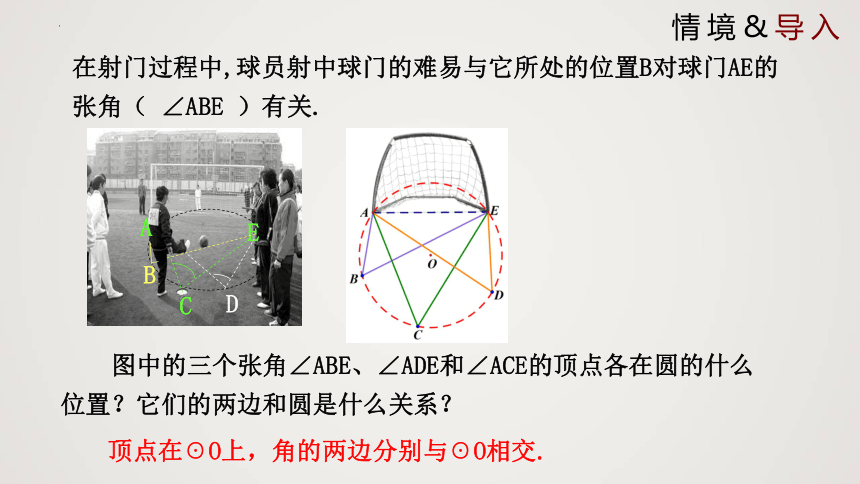
在射门过程中,球员射中球门的难易与它所处的位置B对球门AE的张角( ∠ABE )有关.
图中的三个张角∠ABE、∠ADE和∠ACE的顶点各在圆的什么位置?它们的两边和圆是什么关系?
C
A
E
D
B
顶点在☉O上,角的两边分别与☉O相交.
探索&交流
圆周角定义:
顶点在圆上,并且两边分别与圆还有一个交点的角叫做圆周角.
特征 圆周角必须满足两个条件:
①顶点在圆上;②两边都和圆相交.
探索&交流
特别提醒
圆心角与圆周角的区别与联系:
名称 圆心角 圆周角
区 别 顶点在圆心 顶点在圆上
在同圆中,一条弧所对的圆心角唯一 在同圆中,一条弧所对的圆周角有无数个
联系 两边都与圆相交 例题&解析
例题欣赏
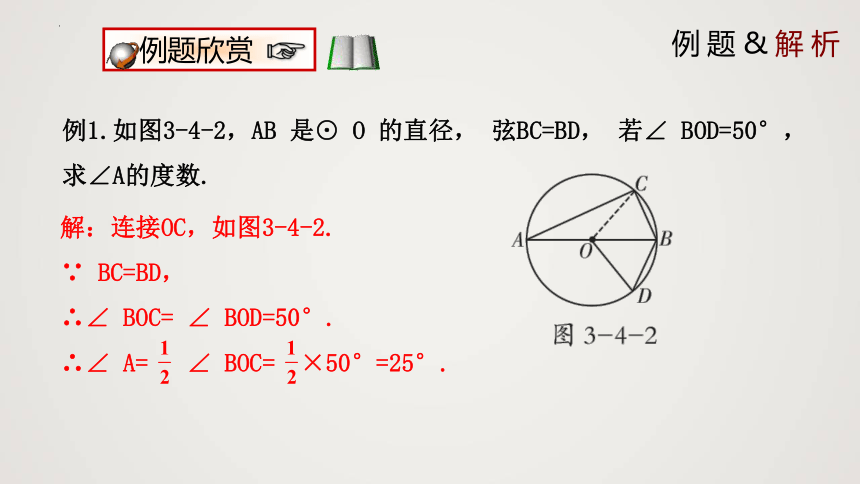
例1.如图3-4-2,AB 是⊙ O 的直径, 弦BC=BD, 若∠ BOD=50°,求∠A的度数.
解:连接OC,如图3-4-2.
∵ BC=BD,
∴∠ BOC= ∠ BOD=50°.
∴∠ A= ∠ BOC= ×50°=25°.
探索&交流
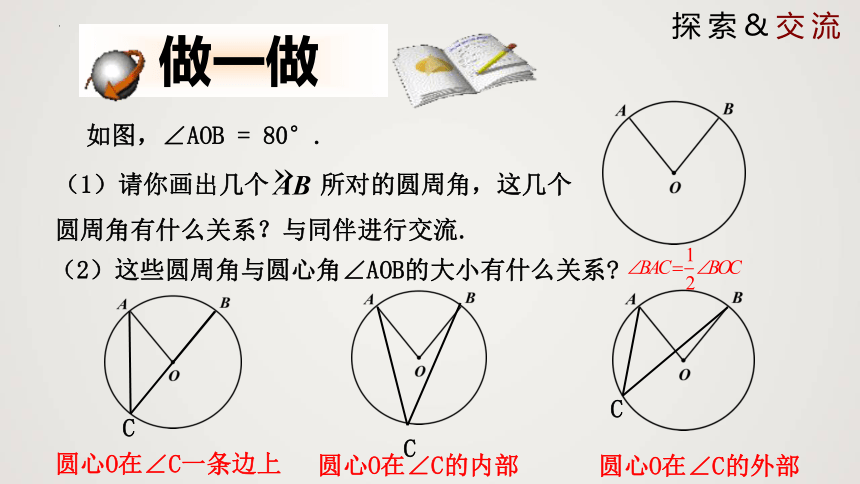
做一做
如图,∠AOB = 80°.
(1)请你画出几个 所对的圆周角,这几个圆周角有什么关系?与同伴进行交流.
(2)这些圆周角与圆心角∠AOB的大小有什么关系
C
圆心O在∠C一条边上
C
圆心O在∠C的内部
C
圆心O在∠C的外部
探索&交流
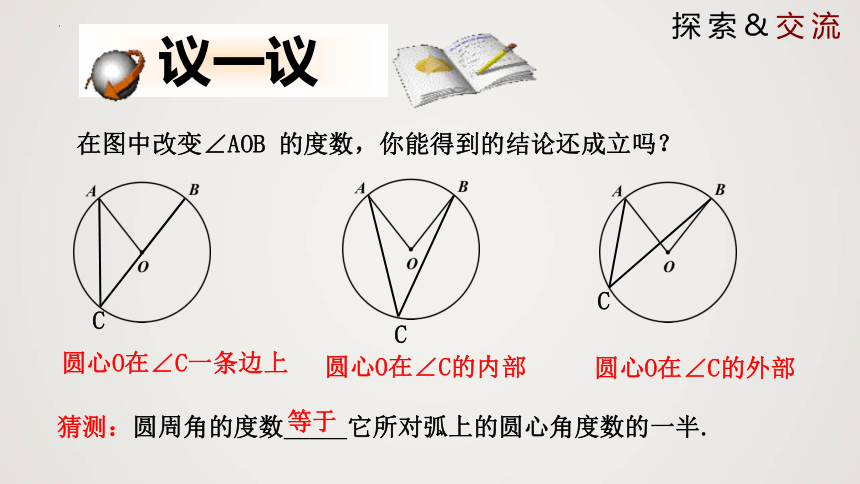
议一议
在图中改变∠AOB 的度数,你能得到的结论还成立吗?
C
圆心O在∠C一条边上
C
圆心O在∠C的内部
C
圆心O在∠C的外部
猜测:圆周角的度数_____它所对弧上的圆心角度数的一半.
等于
探索&交流
已知:在圆O中,弧AB所对的圆周角是∠C,弧AB圆心角是∠AOB.
求证:
过点C作直径CD.由已证可得:
C
D
圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
探索&交流
C
圆心O在∠C一条边上
C
圆心O在∠C的内部
C
圆心O在∠C的外部
C
已知:如图,∠C 是弧AB 所对的圆周角,∠AOB 是弧AB所对的圆心角.
求证:
证明:圆心 O 在∠C 的一条边上,如图.
∵ ∠AOB 是△AOC 的外角,
∴ ∠AOB = ∠A +∠C.
∵ OA = OC,
∴ ∠A =∠C.
∴ ∠AOB = 2∠C,
探索&交流
探索&交流
C
已知:如图,∠C 是弧AB所对的圆周角,∠AOB是弧AB所对的圆心角.
求证:
D
证明:过点C作直径CD.由已证可得:
圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
如图3-4-1,∠ ACB= ∠ AOB.
特别警示:定理中的圆周角与圆心角是
通过它们所对的同一条弧联系在一起的,
故不能把同一条弧这个前提省略.
探索&交流
例题&解析
例题欣赏
例2.如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
C
探索&交流
想一想
在射门游戏中,球员射中球门的难易程度与他所处的位置 B 对球门 AC 的张角(∠ABC)有关.
当球员在 B,D,E 处射门时,他所处的位置对球门 AC 分别形成三个张角∠ABC,∠ADC,∠AEC . 这三个角的大小有什么关系?
A
B
D
E
C
探索&交流
所以 ∠ABC = ∠ADC = ∠AEC .
根据圆周角定理,
●
O
探索&交流
推论 同弧或等弧所对的圆周角相等.
●
O
特别提醒
“同弧或等弧”若改为“同弦或等弦”结论就不成立了.
因为一条弦(非直径)所对的圆周角有两种情况:优弧上的圆周角和劣弧上的圆周角.
例题&解析
例题欣赏
例3.如图3-4-3,A,P,B,C 是圆上的四个点,∠APC=∠CPB=60°.
求证:△ ABC 是等边三角形.
证明:∵ A,P,B,C 是圆上的四个点,
∴∠ ABC= ∠ APC,∠ CPB= ∠ BAC.
又∵∠ APC= ∠ CPB=60°,
∴∠ ABC= ∠ BAC=60°.
∴△ ABC 是等边三角形.
练习&巩固
1.如图,在⊙ O 中,弦AB,CD 相交于点P. 若∠ A=48°,∠ APD=80°,则∠ B 的大小为( )
A. 32°
B. 45°
C. 52°
D. 62°
练习&巩固
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=48°, 则∠AOB= .
B
A
C
O
练习&巩固
3.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
小结&反思
(1)概念(圆周角);
(2)定理:一条弧所对的圆周角等于该弧所对的圆心角的一半;
(3)推论:同圆内,同弧或等弧所对的圆周角相等. 相等的圆周角所对的弧相等;
圆周角和圆心角的关系
第三章 圆
北师大版九年级数学下册
4.1 圆周角和圆心角的关系
学习&目标
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简单的几何问题.(重点)
3.了解圆周角的分类,会推理验证“圆周角与圆心角的关系”.(难点)
情境&导入
1.圆心角的定义
顶点在圆心的角叫圆心角.
2.圆心角的度数和它所对的弧的度数有何关系
如图:∠AOB 弧AB的度数
=
3.在同圆或等圆中,如果两个圆心角、两条___、两条___中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧
弦
情境&导入
在射门过程中,球员射中球门的难易与它所处的位置B对球门AE的张角( ∠ABE )有关.
图中的三个张角∠ABE、∠ADE和∠ACE的顶点各在圆的什么位置?它们的两边和圆是什么关系?
C
A
E
D
B
顶点在☉O上,角的两边分别与☉O相交.
探索&交流
圆周角定义:
顶点在圆上,并且两边分别与圆还有一个交点的角叫做圆周角.
特征 圆周角必须满足两个条件:
①顶点在圆上;②两边都和圆相交.
探索&交流
特别提醒
圆心角与圆周角的区别与联系:
名称 圆心角 圆周角
区 别 顶点在圆心 顶点在圆上
在同圆中,一条弧所对的圆心角唯一 在同圆中,一条弧所对的圆周角有无数个
联系 两边都与圆相交 例题&解析
例题欣赏
例1.如图3-4-2,AB 是⊙ O 的直径, 弦BC=BD, 若∠ BOD=50°,求∠A的度数.
解:连接OC,如图3-4-2.
∵ BC=BD,
∴∠ BOC= ∠ BOD=50°.
∴∠ A= ∠ BOC= ×50°=25°.
探索&交流
做一做
如图,∠AOB = 80°.
(1)请你画出几个 所对的圆周角,这几个圆周角有什么关系?与同伴进行交流.
(2)这些圆周角与圆心角∠AOB的大小有什么关系
C
圆心O在∠C一条边上
C
圆心O在∠C的内部
C
圆心O在∠C的外部
探索&交流
议一议
在图中改变∠AOB 的度数,你能得到的结论还成立吗?
C
圆心O在∠C一条边上
C
圆心O在∠C的内部
C
圆心O在∠C的外部
猜测:圆周角的度数_____它所对弧上的圆心角度数的一半.
等于
探索&交流
已知:在圆O中,弧AB所对的圆周角是∠C,弧AB圆心角是∠AOB.
求证:
过点C作直径CD.由已证可得:
C
D
圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
探索&交流
C
圆心O在∠C一条边上
C
圆心O在∠C的内部
C
圆心O在∠C的外部
C
已知:如图,∠C 是弧AB 所对的圆周角,∠AOB 是弧AB所对的圆心角.
求证:
证明:圆心 O 在∠C 的一条边上,如图.
∵ ∠AOB 是△AOC 的外角,
∴ ∠AOB = ∠A +∠C.
∵ OA = OC,
∴ ∠A =∠C.
∴ ∠AOB = 2∠C,
探索&交流
探索&交流
C
已知:如图,∠C 是弧AB所对的圆周角,∠AOB是弧AB所对的圆心角.
求证:
D
证明:过点C作直径CD.由已证可得:
圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
如图3-4-1,∠ ACB= ∠ AOB.
特别警示:定理中的圆周角与圆心角是
通过它们所对的同一条弧联系在一起的,
故不能把同一条弧这个前提省略.
探索&交流
例题&解析
例题欣赏
例2.如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
C
探索&交流
想一想
在射门游戏中,球员射中球门的难易程度与他所处的位置 B 对球门 AC 的张角(∠ABC)有关.
当球员在 B,D,E 处射门时,他所处的位置对球门 AC 分别形成三个张角∠ABC,∠ADC,∠AEC . 这三个角的大小有什么关系?
A
B
D
E
C
探索&交流
所以 ∠ABC = ∠ADC = ∠AEC .
根据圆周角定理,
●
O
探索&交流
推论 同弧或等弧所对的圆周角相等.
●
O
特别提醒
“同弧或等弧”若改为“同弦或等弦”结论就不成立了.
因为一条弦(非直径)所对的圆周角有两种情况:优弧上的圆周角和劣弧上的圆周角.
例题&解析
例题欣赏
例3.如图3-4-3,A,P,B,C 是圆上的四个点,∠APC=∠CPB=60°.
求证:△ ABC 是等边三角形.
证明:∵ A,P,B,C 是圆上的四个点,
∴∠ ABC= ∠ APC,∠ CPB= ∠ BAC.
又∵∠ APC= ∠ CPB=60°,
∴∠ ABC= ∠ BAC=60°.
∴△ ABC 是等边三角形.
练习&巩固
1.如图,在⊙ O 中,弦AB,CD 相交于点P. 若∠ A=48°,∠ APD=80°,则∠ B 的大小为( )
A. 32°
B. 45°
C. 52°
D. 62°
练习&巩固
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=48°, 则∠AOB= .
B
A
C
O
练习&巩固
3.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB
B.CE=EO
C.∠OCE=40°
D.∠BOC=2∠BAD
小结&反思
(1)概念(圆周角);
(2)定理:一条弧所对的圆周角等于该弧所对的圆心角的一半;
(3)推论:同圆内,同弧或等弧所对的圆周角相等. 相等的圆周角所对的弧相等;
圆周角和圆心角的关系
