3.7 切线长定理 课件(共18张PPT)
文档属性
| 名称 | 3.7 切线长定理 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 772.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 16:36:54 | ||
图片预览



文档简介
(共18张PPT)
第三章 圆
北师大版九年级数学下册
7 切线长定理
学习&目标
1.理解切线长的概念.(重点)
2.掌握切线长定理,初步学会运用切线长定理进行计算与证明.(难点)
情境&导入
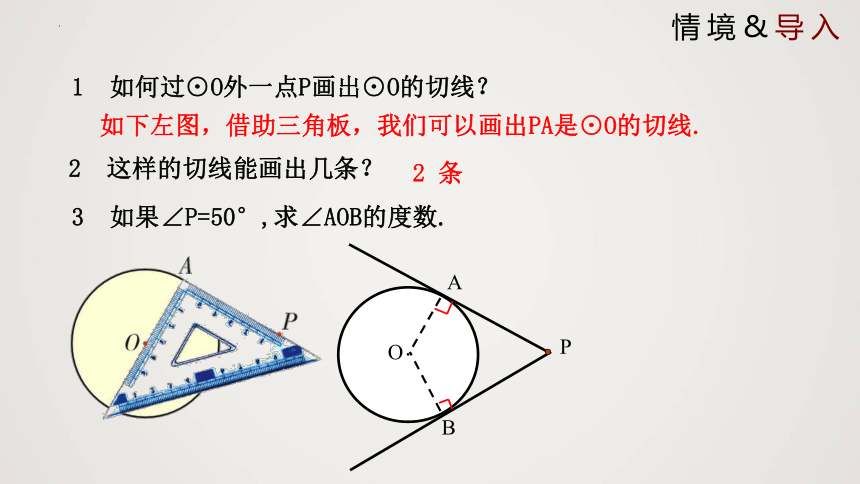
1 如何过⊙O外一点P画出⊙O的切线?
2 这样的切线能画出几条?
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
3 如果∠P=50°,求∠AOB的度数.
·
O
A
B
P
2 条
探索&交流
P
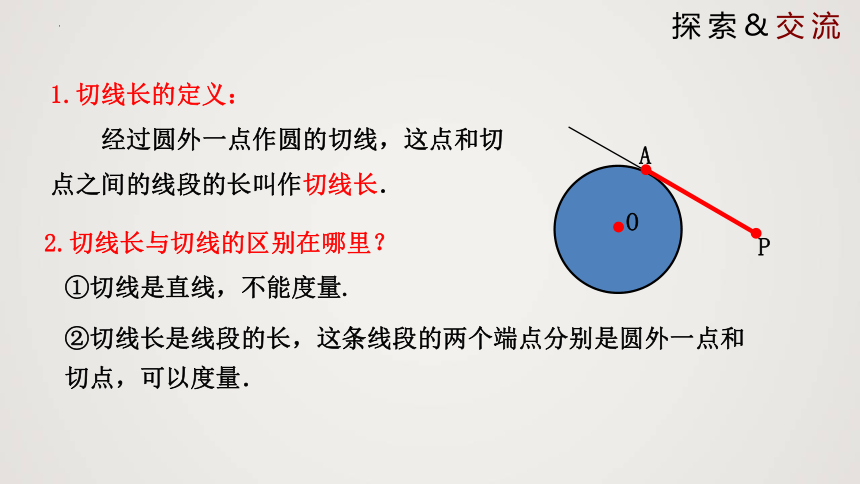
1.切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
探索&交流
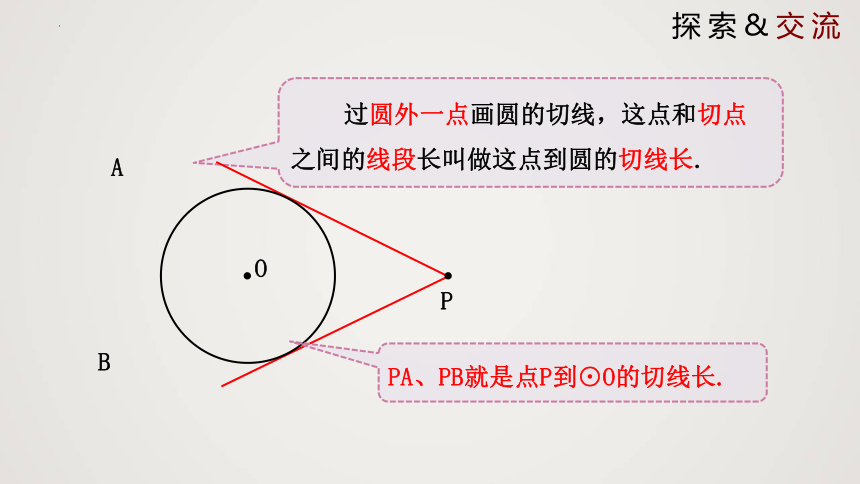
过圆外一点画圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
O
P
A
B
PA、PB就是点P到⊙O的切线长.
探索&交流
O
P
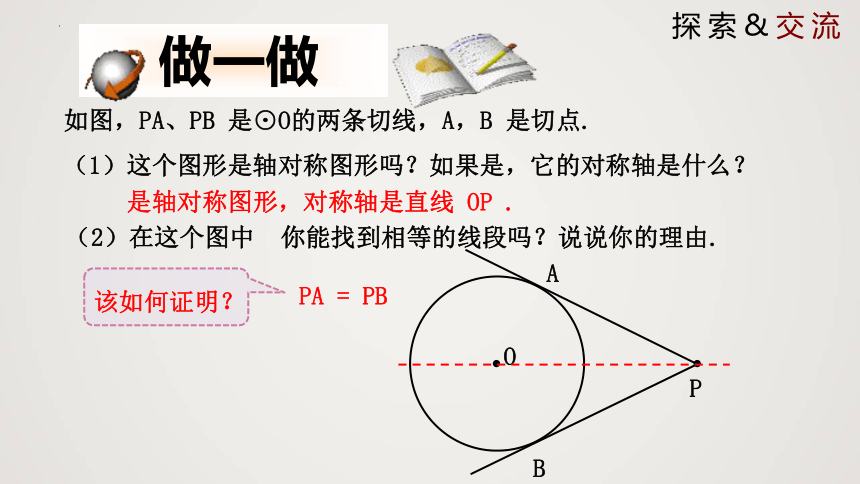
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
A
B
(2)在这个图中 你能找到相等的线段吗?说说你的理由.
PA = PB
该如何证明?
做一做
A
P
O
B
证明:连接OA 、OB 、OP
∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB
用文字语言叙述结论
已知: PA,PB与⊙O相切,点A,B是切点
求证: PA = PB
探索&交流
切线长定理:
过圆外一点引所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
B
P
O
特别提醒
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段的长度相等.
A
探索&交流
示例
如图3-7-1 是切线长定理的一个基本图形, 可以直接得到结论:
(1)PO ⊥ AB;
(2)AO ⊥ AP,BO ⊥ BP;
(3)AP=BP;
(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;
(5)AD=BD;
(6)AC = BC等.
︵
︵
探索&交流
例题&解析
例题欣赏
例1.已知:如图,PA,PB是⊙O的两条切线,A,B是切点。PA=6cm,∠P=60°.则△PAB的周长为 ______.
A
B
P
O
18
例题&解析
例题欣赏
例2.△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
想一想:图中你能找出哪些相等的线段?理由是什么?
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
解得 x=4.
探索&交流
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
E
F
G
H
结论:圆的外切四边形的两组对边的和相等.
即 AD+BC=AB+CD.
例题&解析
例题欣赏
例3.如图,在Rt△ABC 中,∠C = 90°,AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别是 D,E,F,求⊙O 的半径.
B
D
A
F
C
E
O
解:连接 OD,OE,OF,则 OD = OE = OF,设 OD = r.
在 Rt△ABC 中,
AC = 10,BC = 24,
26
r
∵ ⊙O 分别与 AB,BC,AC 相切于点 D,E,F,
∴ OD⊥AB,OE⊥BC,OF⊥AC,BD = BE,AD = AF,CE = CF.
又∵∠C = 90°,
∴ 四边形 OECF 为正方形.
∴ CE = CF = r.
∴ BE = 24 – r,AF = 10 – r.
∴ AB = BD + AD = BE + AF = 34 – 2r.
而 AB = 26,
∴ 34 – 2r = 26.
∴ r = 4,
即 ⊙O 的半径为 4.
例题&解析
练习&巩固
1.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .
A
B
C
O
练习&巩固
2.如图,PA,PB 是⊙ O 的切线,A,B 为切点,若∠ AOB=128 °, 则∠ P 的度数为( )
A.32°
B.52°
C.64°
D.72°
练习&巩固
3.△ABC的内切圆☉O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
A
B
C
F
E
D
O
小结&反思
切线的6个性质:
(1)切线和圆只有一个公共点.
(2)切线和圆心的距离等于圆的半径.
(3)切线垂直于过切点的半径.
(4)经过圆心垂直于切线的直线必过切点.
(5)经过切点垂直于切线的直线必过圆心.
(6)切线长定理.
第三章 圆
北师大版九年级数学下册
7 切线长定理
学习&目标
1.理解切线长的概念.(重点)
2.掌握切线长定理,初步学会运用切线长定理进行计算与证明.(难点)
情境&导入
1 如何过⊙O外一点P画出⊙O的切线?
2 这样的切线能画出几条?
如下左图,借助三角板,我们可以画出PA是⊙O的切线.
3 如果∠P=50°,求∠AOB的度数.
·
O
A
B
P
2 条
探索&交流
P
1.切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
2.切线长与切线的区别在哪里?
探索&交流
过圆外一点画圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
O
P
A
B
PA、PB就是点P到⊙O的切线长.
探索&交流
O
P
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
A
B
(2)在这个图中 你能找到相等的线段吗?说说你的理由.
PA = PB
该如何证明?
做一做
A
P
O
B
证明:连接OA 、OB 、OP
∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB
用文字语言叙述结论
已知: PA,PB与⊙O相切,点A,B是切点
求证: PA = PB
探索&交流
切线长定理:
过圆外一点引所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
B
P
O
特别提醒
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点所连的两条线段的长度相等.
A
探索&交流
示例
如图3-7-1 是切线长定理的一个基本图形, 可以直接得到结论:
(1)PO ⊥ AB;
(2)AO ⊥ AP,BO ⊥ BP;
(3)AP=BP;
(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;
(5)AD=BD;
(6)AC = BC等.
︵
︵
探索&交流
例题&解析
例题欣赏
例1.已知:如图,PA,PB是⊙O的两条切线,A,B是切点。PA=6cm,∠P=60°.则△PAB的周长为 ______.
A
B
P
O
18
例题&解析
例题欣赏
例2.△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
想一想:图中你能找出哪些相等的线段?理由是什么?
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
解得 x=4.
探索&交流
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
E
F
G
H
结论:圆的外切四边形的两组对边的和相等.
即 AD+BC=AB+CD.
例题&解析
例题欣赏
例3.如图,在Rt△ABC 中,∠C = 90°,AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别是 D,E,F,求⊙O 的半径.
B
D
A
F
C
E
O
解:连接 OD,OE,OF,则 OD = OE = OF,设 OD = r.
在 Rt△ABC 中,
AC = 10,BC = 24,
26
r
∵ ⊙O 分别与 AB,BC,AC 相切于点 D,E,F,
∴ OD⊥AB,OE⊥BC,OF⊥AC,BD = BE,AD = AF,CE = CF.
又∵∠C = 90°,
∴ 四边形 OECF 为正方形.
∴ CE = CF = r.
∴ BE = 24 – r,AF = 10 – r.
∴ AB = BD + AD = BE + AF = 34 – 2r.
而 AB = 26,
∴ 34 – 2r = 26.
∴ r = 4,
即 ⊙O 的半径为 4.
例题&解析
练习&巩固
1.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .
A
B
C
O
练习&巩固
2.如图,PA,PB 是⊙ O 的切线,A,B 为切点,若∠ AOB=128 °, 则∠ P 的度数为( )
A.32°
B.52°
C.64°
D.72°
练习&巩固
3.△ABC的内切圆☉O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .
A
B
C
F
E
D
O
小结&反思
切线的6个性质:
(1)切线和圆只有一个公共点.
(2)切线和圆心的距离等于圆的半径.
(3)切线垂直于过切点的半径.
(4)经过圆心垂直于切线的直线必过切点.
(5)经过切点垂直于切线的直线必过圆心.
(6)切线长定理.
