3.8 圆内接正多边形 课件(共21张PPT)
文档属性
| 名称 | 3.8 圆内接正多边形 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第三章 圆
北师大版九年级数学下册
8 圆内接正多边形
学习&目标
1.了解正多边形的概念、正多边形和圆的关系,并能进行有关计算.(重点)
2.正多边形的半径、边心距及边长的计算问题转化为解直角三角形的问题.(难点)
情境&导入
观看大屏幕上这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗
探索&交流
什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
注意
正多边形
各边相等
各角相等
缺一不可
问题1
问题2
探索&交流
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
问题3
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
归纳
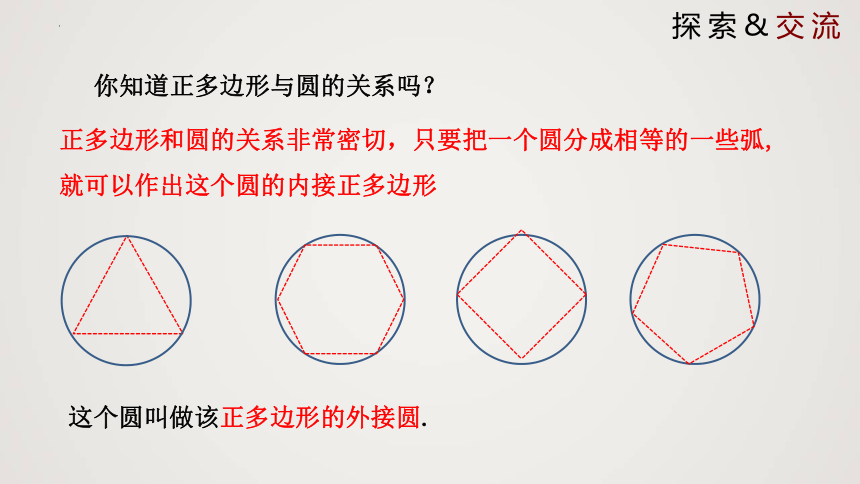
你知道正多边形与圆的关系吗?
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形
探索&交流
这个圆叫做该正多边形的外接圆.
怎样由圆得到多边形呢?
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
—多边形是正多边形
将圆n(n≥3)等分,依次连接各等分点,所得到的多边形是正多边形吗?
弧相等—
将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正n边形的各顶点n等分其外接圆.
归纳
探索&交流
例题&解析
例题欣赏
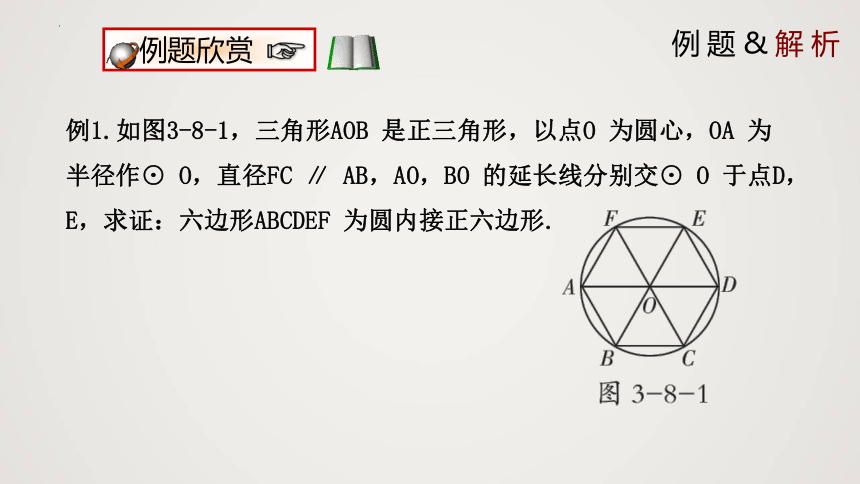
例1.如图3-8-1,三角形AOB 是正三角形,以点O 为圆心,OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O 于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
证明:∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB, ∴ ∠ FOA= ∠ OAB=60 °,
∠ COB= ∠ OBA=60°.
∴ ∠ AOB= ∠ BOC= ∠ COD= ∠ DOE= ∠ EOF=
∠ FOA=60°.∴AB = BC = CD = DE = EF = FA .
∴六边形ABCDEF 为圆内接正六边形.
︵
︵
︵
︵
︵
︵
例题&解析
探索&交流
如图,五边形ABCDE是⊙O的内接正五边形.
E
A
B
C
D
O
圆心O叫做这个正五边形的中心.
OA是这个正五边形的半径.
∠AOB是这个正五边形的中心角.
M
OM是这个正五边形的边心距.
探索&交流
问题1 正n边形的中心角怎么计算?
C
D
O
B
E
F
A
P
问题2 正n边形的边长a,半径R,边心距r之间有什么关系?
a
R
r
问题3 边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
例题&解析
例题欣赏
例2.如图,正五边形ABCDE内接于⊙O,则∠ADE的度数是 ( )
A.60° B.45° C. 36° D. 30°
C
·
A
B
C
D
E
O
例题&解析
例题欣赏
例3.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为G,求这个正六边形的中心角、边长和边心距.
A
B
C
D
E
F
O
G
解:连接 OD.
∵ 六边形 ABCDEF 为正六边形,
∴ △COD 为等边三角形.
∴ CD = OC = 4 .
在Rt△COG 中,OC = 4,
∴ 正六边形 ABCDEF 的中心角为60°,边长为 4,边心距为
例题&解析
探索&交流
如何用尺规作一个已知圆的内接正六边形呢?
O
方法一:由于正六边形的中心角为60°,因此它的边长就是其外接圆的半径 R . 所以,在半径为 R 的圆上,依次截取等于 R 的弦,就可以六等分圆,进而作出圆内接正六边形.
R
分别以F,C为圆心,以⊙O的半径R为半径作弧,
与⊙O相交于点E,A和D,B,则 A,B,C,D,E,F 是 ⊙O的六等分点,顺次连接AB,BC,CD,DE,EF,FA,便得到正六边形ABCDEF.
方法二:作⊙O的任意一条直径FC,
O
F
C
E
A
D
B
探索&交流
例题&解析
例题欣赏
例4.作一个正三角形,使其半径为0.9 cm.
解:(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的
正三角形,如图所示.
练习&巩固
1.若一个四边形的外接圆与内切圆是同心圆,则这个四边形一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 不能确定
练习&巩固
2.如图,正六边形ABCDEF 内接于⊙ O,若⊙ O 的周长等于6π. 则正六边形的边长为( )
练习&巩固
3.下列说法正确的是( )
A.各边都相等的多边形是正多边形
B.一个圆有且只有一个内接正多边形
C.圆内接正四边形的边长等于半径
D.圆内接正n边形的中心角度数为
小结&反思
1.正多边形和圆的有关概念:正多边形的中心,正多边形的半径,正多边形的中心角,正多边形的边心距.
2.正多边形的半径、正多边形的中心角、边长,正多边形的边心距之间的等量关系.
通过本课时的学习,需要我们掌握:
第三章 圆
北师大版九年级数学下册
8 圆内接正多边形
学习&目标
1.了解正多边形的概念、正多边形和圆的关系,并能进行有关计算.(重点)
2.正多边形的半径、边心距及边长的计算问题转化为解直角三角形的问题.(难点)
情境&导入
观看大屏幕上这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗
探索&交流
什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
注意
正多边形
各边相等
各角相等
缺一不可
问题1
问题2
探索&交流
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
问题3
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
归纳
你知道正多边形与圆的关系吗?
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形
探索&交流
这个圆叫做该正多边形的外接圆.
怎样由圆得到多边形呢?
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
—多边形是正多边形
将圆n(n≥3)等分,依次连接各等分点,所得到的多边形是正多边形吗?
弧相等—
将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正n边形的各顶点n等分其外接圆.
归纳
探索&交流
例题&解析
例题欣赏
例1.如图3-8-1,三角形AOB 是正三角形,以点O 为圆心,OA 为半径作⊙ O,直径FC ∥ AB,AO,BO 的延长线分别交⊙ O 于点D,E,求证:六边形ABCDEF 为圆内接正六边形.
证明:∵三角形AOB 是正三角形,
∴∠ AOB= ∠ OAB= ∠ OBA=60°,OB=OA.
∴点B 在⊙ O 上.
∵ FC ∥ AB, ∴ ∠ FOA= ∠ OAB=60 °,
∠ COB= ∠ OBA=60°.
∴ ∠ AOB= ∠ BOC= ∠ COD= ∠ DOE= ∠ EOF=
∠ FOA=60°.∴AB = BC = CD = DE = EF = FA .
∴六边形ABCDEF 为圆内接正六边形.
︵
︵
︵
︵
︵
︵
例题&解析
探索&交流
如图,五边形ABCDE是⊙O的内接正五边形.
E
A
B
C
D
O
圆心O叫做这个正五边形的中心.
OA是这个正五边形的半径.
∠AOB是这个正五边形的中心角.
M
OM是这个正五边形的边心距.
探索&交流
问题1 正n边形的中心角怎么计算?
C
D
O
B
E
F
A
P
问题2 正n边形的边长a,半径R,边心距r之间有什么关系?
a
R
r
问题3 边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
例题&解析
例题欣赏
例2.如图,正五边形ABCDE内接于⊙O,则∠ADE的度数是 ( )
A.60° B.45° C. 36° D. 30°
C
·
A
B
C
D
E
O
例题&解析
例题欣赏
例3.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为G,求这个正六边形的中心角、边长和边心距.
A
B
C
D
E
F
O
G
解:连接 OD.
∵ 六边形 ABCDEF 为正六边形,
∴ △COD 为等边三角形.
∴ CD = OC = 4 .
在Rt△COG 中,OC = 4,
∴ 正六边形 ABCDEF 的中心角为60°,边长为 4,边心距为
例题&解析
探索&交流
如何用尺规作一个已知圆的内接正六边形呢?
O
方法一:由于正六边形的中心角为60°,因此它的边长就是其外接圆的半径 R . 所以,在半径为 R 的圆上,依次截取等于 R 的弦,就可以六等分圆,进而作出圆内接正六边形.
R
分别以F,C为圆心,以⊙O的半径R为半径作弧,
与⊙O相交于点E,A和D,B,则 A,B,C,D,E,F 是 ⊙O的六等分点,顺次连接AB,BC,CD,DE,EF,FA,便得到正六边形ABCDEF.
方法二:作⊙O的任意一条直径FC,
O
F
C
E
A
D
B
探索&交流
例题&解析
例题欣赏
例4.作一个正三角形,使其半径为0.9 cm.
解:(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°;
(3)连接 AB,BC,CA.则△ABC为所求作的
正三角形,如图所示.
练习&巩固
1.若一个四边形的外接圆与内切圆是同心圆,则这个四边形一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 不能确定
练习&巩固
2.如图,正六边形ABCDEF 内接于⊙ O,若⊙ O 的周长等于6π. 则正六边形的边长为( )
练习&巩固
3.下列说法正确的是( )
A.各边都相等的多边形是正多边形
B.一个圆有且只有一个内接正多边形
C.圆内接正四边形的边长等于半径
D.圆内接正n边形的中心角度数为
小结&反思
1.正多边形和圆的有关概念:正多边形的中心,正多边形的半径,正多边形的中心角,正多边形的边心距.
2.正多边形的半径、正多边形的中心角、边长,正多边形的边心距之间的等量关系.
通过本课时的学习,需要我们掌握:
