19.1.2函数的图象 课件(共32张PPT)
文档属性
| 名称 | 19.1.2函数的图象 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 10:22:35 | ||
图片预览







文档简介
(共32张PPT)
第19.1.2 函数的图象
人教版数学八年级下册
学习目标
1.理解函数的图象的概念.
2.能画出一些简单的函数图象.
3.能根据所给函数图象读出一些有用的信息.
4.能对函数关系进行分析,对变量的变化情况进行初步讨论.
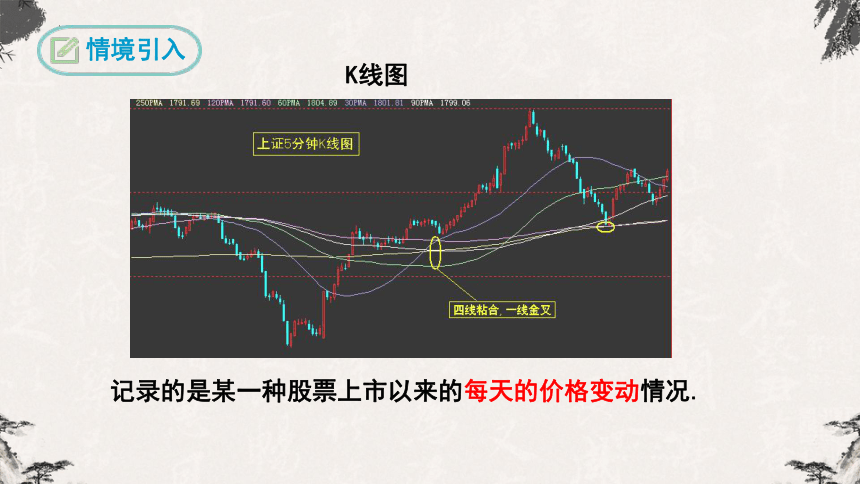
记录的是某一种股票上市以来的每天的价格变动情况.
K线图
情境引入
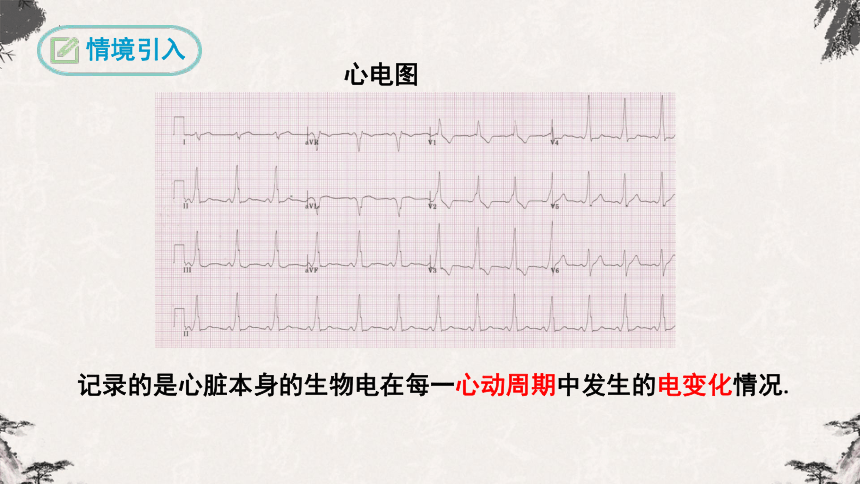
情境引入
心电图
记录的是心脏本身的生物电在每一心动周期中发生的电变化情况.
互动新授
有些问题中的函数关系很难列式子表示,但是可以用图来直观地反映,例如用心电图表示心脏部位的生物电流与时间的关系.
即使对于能列式表示的函数关系,如果也能画图表示,那么会使函数关系更直观.
互动新授
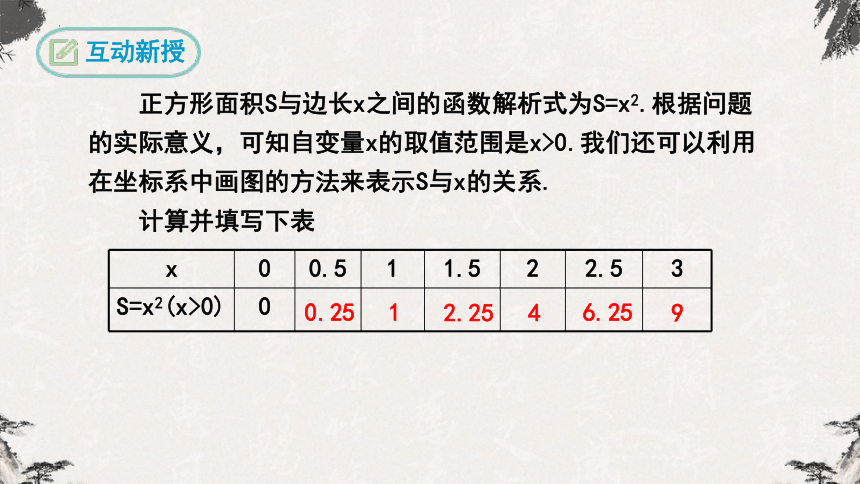
正方形面积S与边长x之间的函数解析式为S=x2.根据问题的实际意义,可知自变量x的取值范围是x>0.我们还可以利用在坐标系中画图的方法来表示S与x的关系.
计算并填写下表
x 0 0.5 1 1.5 2 2.5 3
S=x2(x>0) 0
0.25
1
2.25
4
6.25
9
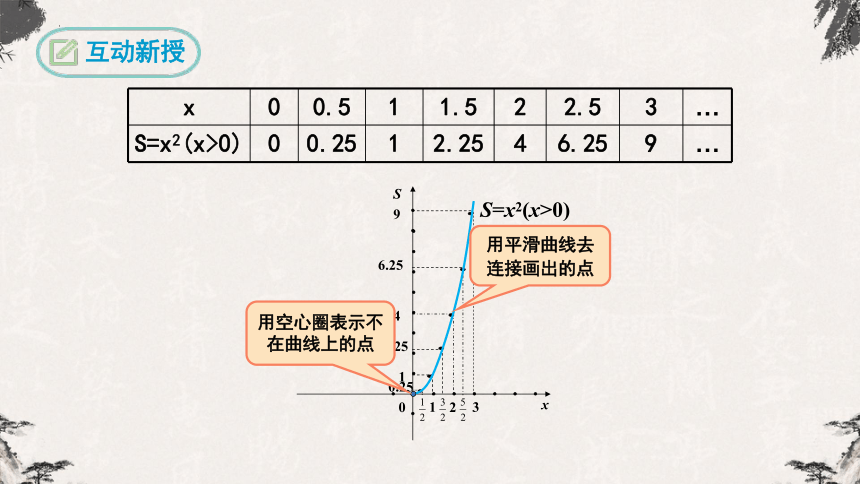
互动新授
x 0 0.5 1 1.5 2 2.5 3 …
S=x2(x>0) 0 0.25 1 2.25 4 6.25 9 …
1
4
9
0
2
1
3
2.25
S
6.25
0.25
x
S=x2(x>0)
用平滑曲线去连接画出的点
用空心圈表示不在曲线上的点
互动新授
函数的图象的定义:
一般地,对于一个函数,如果把自变量和函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
上图的曲线即函数S=x2(x>0)的图象.
互动新授
思考 如图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化.你从图象中得到了哪些信息?
-3
O
4
14
24
8
T/℃
t/h
互动新授
-3
O
4
14
24
8
T/℃
t/h
可以认为,气温T是时间t的函数,上图是这个函数的图象.由图象可知:
(1)这一天中凌晨4时气温最低(-3℃),14时气温最高(8℃).
(2)从0时至4时气温呈下降状态,从4时至14时气温呈上升状态,从14时至24时气温又呈下降状态.
(3)我们可以从图象中看出这一天中任一时刻的气温大约是多少.
典例精析
例2 如图所示,小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离家的距离y与时间x之间的关系.
根据图象回答下列问题:
(1).食堂离小明家多远?小明从家到食堂用了多少时间?
(2).小明在食堂吃早餐用了多少时间?
(3).食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(4).小明读报用了多长时间?
(5).图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
典例精析
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:(1).0.6km;8min.
(2).17min.
(3).0.2km;3min.
(4).30min.
(5).0.8km;0.08 km/min.
典例精析
例3 在下列式子中,对于 x的每一个确定的值,y有唯一的对应值,即y是x的函数. 画出这些函数的图象:
(1)y=x+0.5; (2) (x>0).
x … -3 -2 -1 0 1 2 3 …
y … …
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些数值,算出y的对应值,列表(计算并填写表中空格):
全体实数
-0.5 0.5 1.5 2.5
-2.5
-1.5
3.5
典例精析
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=x+0.5
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
从函数图象可以看出,直线从左到右上升,即当x由小变大时,y=x+0.5 .
画出的图象是一条 ,
直线
随之增大
典例精析
(2) (x>0).
解:(2)列表(计算并填写下表).
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 3 2 1.5 …
12
4
2.4
1.2
1
典例精析
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
描点:分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.
连线:用光滑的曲线把这些点依次连接起来.
( x >0).
当自变量的值由小变大时,
对应的函数值 .
随之减小
总结归纳
第一步,列表—表中给出一些自变量的值及其 ;
第二步,描点—在平面直角坐标系中,以自变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
第三步:连线—按照横坐标 的顺序,把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
描点法画函数图象的一般步骤如下:
总结归纳
由上可知,写出函数的解析式,或者列表格,或者画函数图象,都可以表示具体的 函数.这三种表示函数的方法,分别称为解析式法、列表法、图象法.
思考
从前面的例子看,你认为三种表示函数的方法各有什么优点?
总结归纳
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系,对某些特定数值带来一目了然的效果. 例如:火车时刻表.
3.图象法:直观地反映了函数随自变量的变化而变化的规律,而且对于一些无法用解析式表达的函数,图象可充当重要的角色. 例如:自动测温曲线.
提示:在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.
典例精析
例4 一水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
解:(1)可以看出,这6个点 ,且每小时水位 .由此猜想,在这个时间段中水位可能是以同一速度均匀上升的
典例精析
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
在同一直线上
上升0.3m
5
A
B
(2)水位高度y是否为时间t的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
解:(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.函数解析式为: .
自变量的取值范围是: .它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=3+0.3t
0≤t≤5
5
0.3m/h
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
典例精析
典例精析
(3)据估计这种上涨规律还会持续2h,预测再过2h水位高度将达到多少m.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
解:(3)如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
由例题可以看出函数的不同表示法之间可以 .
互相转化
1.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
C
小试牛刀
1.某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(h)的函数关系如图所示.
(1)根据图象填空:①___先完成一天的生产任务;在生产过程中,____因机器故障停止生产____h;
②当t=_______ 时,甲、乙生产的零件个数相等.
甲
甲
2
3或5.5
课堂检测
2.最近我市连降雨雪,水库水位上涨.如图表示某一天水位变化情况,0时的水位为警戒水位.结合图象判断下列叙述不正确的是 ( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
C
课堂检测
1.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离(s)是时间(t)的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
是
S=200-25t
拓展训练
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
拓展训练
图象的画法
图象表达的实际意义
描点
列表
连线
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
函数的图象
函数的
表示方法
课堂小结
1.小明所在学校与家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.如图,能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系图象的是( )
D
课后作业
2. 已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm.
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少
解:
(x>0).
(2)当x=10时,y=60÷10=6
∴当底边长为10cm时,底边上的高是6cm.
x
y=
60
(1)
课后作业
谢谢聆听
第19.1.2 函数的图象
人教版数学八年级下册
学习目标
1.理解函数的图象的概念.
2.能画出一些简单的函数图象.
3.能根据所给函数图象读出一些有用的信息.
4.能对函数关系进行分析,对变量的变化情况进行初步讨论.
记录的是某一种股票上市以来的每天的价格变动情况.
K线图
情境引入
情境引入
心电图
记录的是心脏本身的生物电在每一心动周期中发生的电变化情况.
互动新授
有些问题中的函数关系很难列式子表示,但是可以用图来直观地反映,例如用心电图表示心脏部位的生物电流与时间的关系.
即使对于能列式表示的函数关系,如果也能画图表示,那么会使函数关系更直观.
互动新授
正方形面积S与边长x之间的函数解析式为S=x2.根据问题的实际意义,可知自变量x的取值范围是x>0.我们还可以利用在坐标系中画图的方法来表示S与x的关系.
计算并填写下表
x 0 0.5 1 1.5 2 2.5 3
S=x2(x>0) 0
0.25
1
2.25
4
6.25
9
互动新授
x 0 0.5 1 1.5 2 2.5 3 …
S=x2(x>0) 0 0.25 1 2.25 4 6.25 9 …
1
4
9
0
2
1
3
2.25
S
6.25
0.25
x
S=x2(x>0)
用平滑曲线去连接画出的点
用空心圈表示不在曲线上的点
互动新授
函数的图象的定义:
一般地,对于一个函数,如果把自变量和函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
上图的曲线即函数S=x2(x>0)的图象.
互动新授
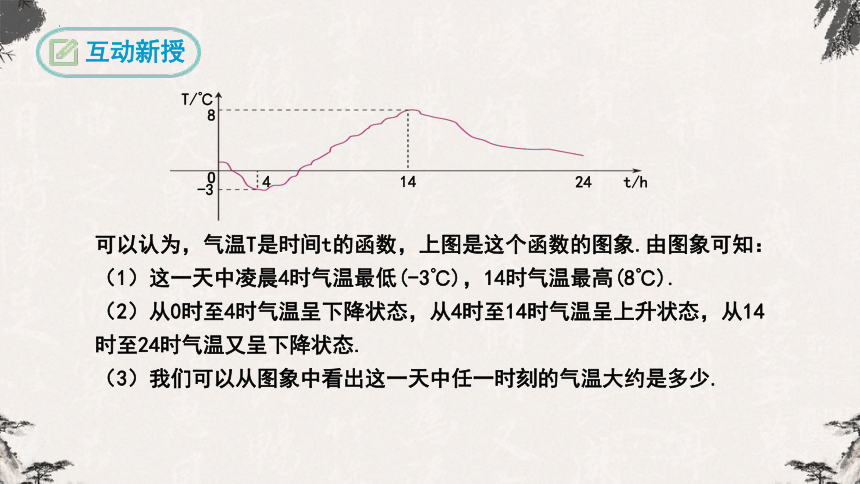
思考 如图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化.你从图象中得到了哪些信息?
-3
O
4
14
24
8
T/℃
t/h
互动新授
-3
O
4
14
24
8
T/℃
t/h
可以认为,气温T是时间t的函数,上图是这个函数的图象.由图象可知:
(1)这一天中凌晨4时气温最低(-3℃),14时气温最高(8℃).
(2)从0时至4时气温呈下降状态,从4时至14时气温呈上升状态,从14时至24时气温又呈下降状态.
(3)我们可以从图象中看出这一天中任一时刻的气温大约是多少.
典例精析
例2 如图所示,小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程中,小明离家的距离y与时间x之间的关系.
根据图象回答下列问题:
(1).食堂离小明家多远?小明从家到食堂用了多少时间?
(2).小明在食堂吃早餐用了多少时间?
(3).食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(4).小明读报用了多长时间?
(5).图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
典例精析
8
25
28
58
68
x/min
0.8
0.6
y/km
O
解:(1).0.6km;8min.
(2).17min.
(3).0.2km;3min.
(4).30min.
(5).0.8km;0.08 km/min.
典例精析
例3 在下列式子中,对于 x的每一个确定的值,y有唯一的对应值,即y是x的函数. 画出这些函数的图象:
(1)y=x+0.5; (2) (x>0).
x … -3 -2 -1 0 1 2 3 …
y … …
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些数值,算出y的对应值,列表(计算并填写表中空格):
全体实数
-0.5 0.5 1.5 2.5
-2.5
-1.5
3.5
典例精析
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=x+0.5
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
从函数图象可以看出,直线从左到右上升,即当x由小变大时,y=x+0.5 .
画出的图象是一条 ,
直线
随之增大
典例精析
(2) (x>0).
解:(2)列表(计算并填写下表).
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 3 2 1.5 …
12
4
2.4
1.2
1
典例精析
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
描点:分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.
连线:用光滑的曲线把这些点依次连接起来.
( x >0).
当自变量的值由小变大时,
对应的函数值 .
随之减小
总结归纳
第一步,列表—表中给出一些自变量的值及其 ;
第二步,描点—在平面直角坐标系中,以自变量的值为 ,相应的函数值为 ,描出表格中数值对应的各点;
第三步:连线—按照横坐标 的顺序,把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
描点法画函数图象的一般步骤如下:
总结归纳
由上可知,写出函数的解析式,或者列表格,或者画函数图象,都可以表示具体的 函数.这三种表示函数的方法,分别称为解析式法、列表法、图象法.
思考
从前面的例子看,你认为三种表示函数的方法各有什么优点?
总结归纳
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系,对某些特定数值带来一目了然的效果. 例如:火车时刻表.
3.图象法:直观地反映了函数随自变量的变化而变化的规律,而且对于一些无法用解析式表达的函数,图象可充当重要的角色. 例如:自动测温曲线.
提示:在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.
典例精析
例4 一水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
解:(1)可以看出,这6个点 ,且每小时水位 .由此猜想,在这个时间段中水位可能是以同一速度均匀上升的
典例精析
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
在同一直线上
上升0.3m
5
A
B
(2)水位高度y是否为时间t的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
解:(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.函数解析式为: .
自变量的取值范围是: .它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=3+0.3t
0≤t≤5
5
0.3m/h
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
典例精析
典例精析
(3)据估计这种上涨规律还会持续2h,预测再过2h水位高度将达到多少m.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
解:(3)如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
由例题可以看出函数的不同表示法之间可以 .
互相转化
1.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
C
小试牛刀
1.某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(h)的函数关系如图所示.
(1)根据图象填空:①___先完成一天的生产任务;在生产过程中,____因机器故障停止生产____h;
②当t=_______ 时,甲、乙生产的零件个数相等.
甲
甲
2
3或5.5
课堂检测
2.最近我市连降雨雪,水库水位上涨.如图表示某一天水位变化情况,0时的水位为警戒水位.结合图象判断下列叙述不正确的是 ( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
C
课堂检测
1.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离(s)是时间(t)的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
是
S=200-25t
拓展训练
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
拓展训练
图象的画法
图象表达的实际意义
描点
列表
连线
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
函数的图象
函数的
表示方法
课堂小结
1.小明所在学校与家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.如图,能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系图象的是( )
D
课后作业
2. 已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm.
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少
解:
(x>0).
(2)当x=10时,y=60÷10=6
∴当底边长为10cm时,底边上的高是6cm.
x
y=
60
(1)
课后作业
谢谢聆听
