7.1 正切 课件（共24张PPT）

正切
Tangent
苏科版九年级下册第7章锐角函数
教学目标
01
认识锐角的正切的概念，能熟练运用正切公式进行计算
02
熟记特殊角度的正切值
03
理解锐角的正切值会随锐角的增大而增大
正切的定义
知识精讲
情境引入
01
Q1：小明家刚建了新房子，请帮他选择相对安全的楼梯进行搭建
【分析】右侧的楼梯比左侧的“陡”，选择左侧的电梯更安全
知识精讲
情境引入
01
Q2：小明为了感谢你的帮助，邀请你在他家附近的公园里爬坡，
以下哪个坡爬起来更费劲？
【分析】右侧的坡比左侧的“陡”，爬起来更费劲
知识精讲
知识精讲
02
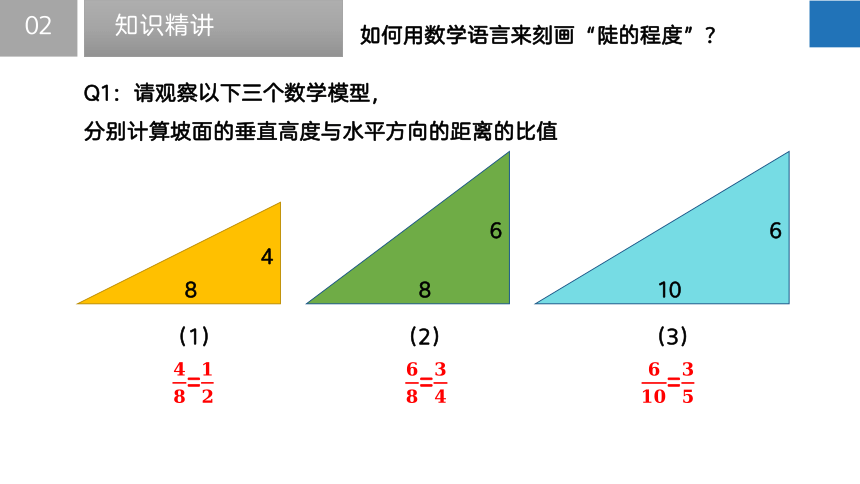
如何用数学语言来刻画“陡的程度”？
4
8
6
8
6
10
（1） （2） （3）
Q1：请观察以下三个数学模型，
分别计算坡面的垂直高度与水平方向的距离的比值
????????=????????
?
????????=????????
?
????????????=????????
?
02
知识精讲
坡度
【坡度的定义】
通常把坡面的垂直高度h与水平方向的距离l的比叫做坡度（或叫做坡比），
坡度越大，坡越陡
知识精讲
知识精讲
02
（1） （2） （3）
4
8
6
8
6
10
????????=????????
?
????????=????????
?
????????????=????????
?
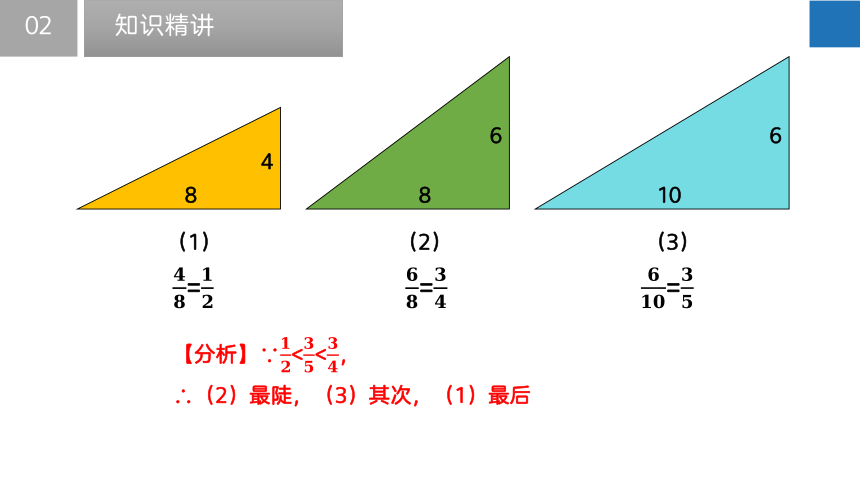
【分析】∵????????∴（2）最陡，（3）其次，（1）最后
?
知识精讲
知识精讲
02
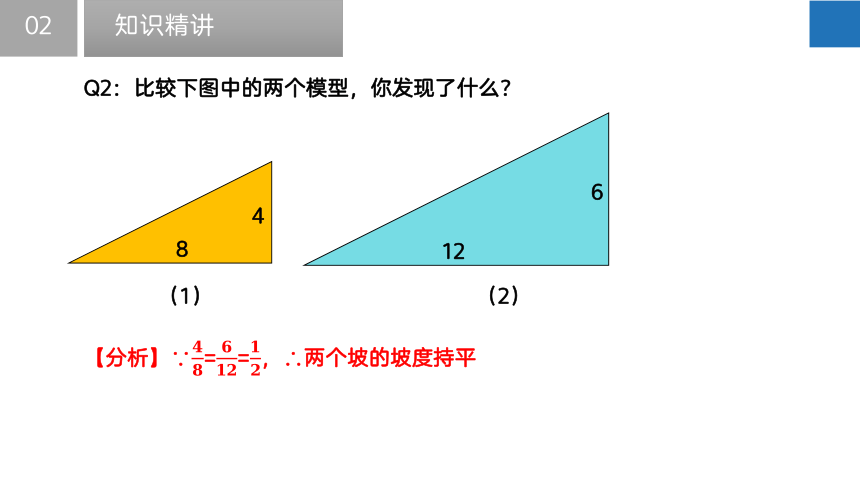
Q2：比较下图中的两个模型，你发现了什么？
【分析】∵????????=????????????=????????，∴两个坡的坡度持平
?
4
8
6
12
（1） （2）
02
知识精讲
Q3：如图，锐角A的大小确定，作出Rt△ABIC1、Rt△AB2C2、Rt△AB3C3，
????????????????????????????、????????????????????????????、????????????????????????????之间有怎样的关系？
?
【分析】Rt△ABIC1∽Rt△AB2C2∽Rt△AB3C3∽……
根据相似三角形性质，得：????????????????????????????????=????????????????????????????=????????????????????????????
?
【总结】如果直角三角形的一个锐角的大小确定，那么这个锐角的对边与邻直角边的比值也确定
02
知识精讲
正切
【正切的定义】
如图，在Rt△ABC中，∠C=90°，
我们把∠A的对边a与邻边b的比，叫做∠A的正切，
记作tanA，tanA=∠A的对边∠A的邻边=ab
?
02
知识精讲
Q4：判断对错
（1）如图，????????????????=???????????????? ( )
（2）如图，????????????????=???????????????? ( )
（3）如图，????????????????=???????????????? ( )
（4）如图，????????????∠????????????=???????? ( )
（5）如图，????????????????=???????? ( )
?
（2）
（1）
A
B
C
A
B
C
A
B
C
（3~5）
4cm
3cm
×
×
×
√
√
02
知识精讲
【注意点】
（1）初中阶段，正切是在直角▲中定义的，研究锐角的正切，且tanA>0
（2）tanA是一个完整的符号，表示∠A的正切，不要误以为是“tan”乘以“A”
（3）∠A的正切的记法中，“A”前面无需加“∠”；但是∠BAC、∠1的正切的记法中，需要加“∠”，即tan∠BAC、tan∠1
（4）tanA的大小只与∠A的大小有关，与直角▲的边长无关（我们只是利用边长计算数值而已）
（5）tanA没有单位，是一个比值，即∠A的对边∠A的邻边，且这里的“邻边”指的是“邻直角边”，不是“斜边”
?
知识精讲
例1、△ABC中，∠C=90°，AB=13，BC=5，tanB的值是（　　）
A．????????????
B．????????????
C．????????????????
D．????????????
?
【分析】如图：
∵∠C=90°，BC=5，AB=13，
∴AC=12，
∴????????????????=????????????????=????????????
?
【正切的定义】
D
5
13
知识精讲
例2、如图，在8×4的矩形网格中，每个小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为__________．
【分析】由图形知：????????????∠????????????=????????=????????
?
????????
?
正切的增减性
知识精讲
情境引入
01
Q1：如图，随着锐角的增大，锐角的正切值如何变化？
（以锐角65°为例：一个点从原点O出发，沿着65°线移动到点P时，这个点沿水平方向前进了1个单位长度，沿垂直方向上升了约2.14个单位长度）
【结论】锐角的正切值会随着锐角的增大而增大
【分析】设从原点O沿着不同角度出发的各个点，水平方向前进的距离都是1个单位长度，
在此情况下，锐角的正切值即垂直方向上升的距离的数值
知识精讲
情境引入
01
Q2：如图，分别计算tan30°，tan45°，tan60°，并比较三个值的大小
????????????????????°=????????=????????
?
30°
45°
60°
1
1
????
?
1
????????????????????°=????????=????
?
????????????????????°=????????=????
?
【结论】tan30°02
知识精讲
特殊角度的正切值与正切的增减性
【正切的增减性】
锐角的正切值会随着锐角的增大而增大
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}tan30°
tan45°
tan60°
????????
1
????
例3、若tanA=2，则∠A的度数估计在（　　）
A．在0°和30°之间 B．在30°和45°之间
C．在45°和60°之间 D．在60°和90°之间
【正切的增减性】
D
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}tan30°
tan45°
tan60°
????????
1
????
例4、若锐角三角函数tan55°=a，则a的范围是（　　）
A．0＜a＜1 B．1＜a＜2 C．2＜a＜3 D．3＜a＜4
B
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}tan30°
tan45°
tan60°
????????
1
????
课后总结
【正切的定义】
如图，在Rt△ABC中，∠C=90°，
我们把∠A的对边a与邻边b的比，叫做∠A的正切，
记作tanA，tanA=∠A的对边∠A的邻边=ab
?
【注意点】
（1）初中阶段，正切是在直角▲中定义的，研究锐角的正切，且tanA>0
（2）tanA是一个完整的符号，表示∠A的正切，不要误以为是“tan”乘以“A”
（3）∠A的正切的记法中，“A”前面无需加“∠”；但是∠BAC、∠1的正切的记法中，需要加“∠”，即tan∠BAC、tan∠1
（4）tanA的大小只与∠A的大小有关，与直角▲的边长无关（我们只是利用边长计算数值而已）
（5）tanA没有单位，是一个比值，即∠A的对边∠A的邻边，且这里的“邻边”指的是“邻直角边”，不是“斜边”
?
课后总结
【正切的增减性】
锐角的正切值会随着锐角的增大而增大
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}tan30°
tan45°
tan60°
????????
1
????
谢谢学习
Thank you for learning