北京 选择题实用解法[下学期]

选择题实用解法谈
　　　　　　　　　
谁都希望自已在选择题的解题中能又快又准确，而要做到这一点，确实不太容易，除了我们要完整地掌握基础知识，基本技能之外，还要能针对选择题的特点，利用一切可以利用的数学信息，灵活巧妙，快速解题，这就需要学习，积累熟练掌握各种的选择题解法，下面我将例举一定数量的选择题，供大家备考练习。为了便于大家先练后校，总结提高，同时也为了避免先入之见，突出发散性思维，在习题组成的顺序中，也不使用专法归类，同时不对直接解法做说明。练习中建议以五个小题为一小组进行，而给大家提供的解法中，往往只突出某种方法，，供大家参考，其实许多题目都有多种解法，，这也给大家共同学习，讨论交流提供了更多的空间。
习题：
1. 已知是第一象限角，且，则是　　（　　　）
A：第一象限角　B：第二象限角　C：第三象限角　D：第四象限角
2、函数的最小正周期是　　　　　　（　　）
A：　　　　B：　　　　C：　　　　　D：
3、不等式的解集是　　　　　　　　　　（　　　）
A：　　B：　　C：　　D：
4、直线与直线互相垂直，则
A：　B：　　C：　　D：
5、双曲线的离心率分别为则的最小值是　　　　　　　　　　　　　　　　　　　（　　　　　）
A：　B：　　C：　　D：
解法参考：（1）特值淘汰法，若取满足意，在第三象限角，选C。
（2）情境简化法，可用做计算，结论与原题无异，选C
（3）比较选择支，特值陶汰法；是原不等式的解，去A，不是原不等的解，去C，满足不等式而，故选B
（4）代入检验法：选C
（5）特例解题，当时，选C
6、若,则最大值是　　　　（　　　）
A：－1　B：　　　C：　　D：
7：的最小正周期是　　（　　　）
A： B：　　　C：　　D：依 取值而定
8：化为积的形式是　　　　　　　　　（　　　）
A：　B：
C：　　D：
9：奇函数满足　（　　）
A：－4　 B：　－2　　C：4　　D：0
10、　　　（　　　）
A：　 B：　4　　C：　　D：
解法参考：
（6）注意到满足换对称性，同题5，当时必取最大值。与5题不同的是，显然可非正值，故必为最大值。选D
（7）情境简化法，选B，事实上，当m=1，选B，一般地，选　B
8：特值陶汰法；取得，代入选择支，易得B
　9：特值陶汰法，取x=0，代入知
10：同5，6，选A，如果不放心，可由，可知最小。
　11、由方程确定的曲线围成的图形面积是　　（　　　　）
　A:1 B:2 C: D:4
解法：情竟简化法，以为新原点移轴，化方程为，在新坐标系中求解。选B
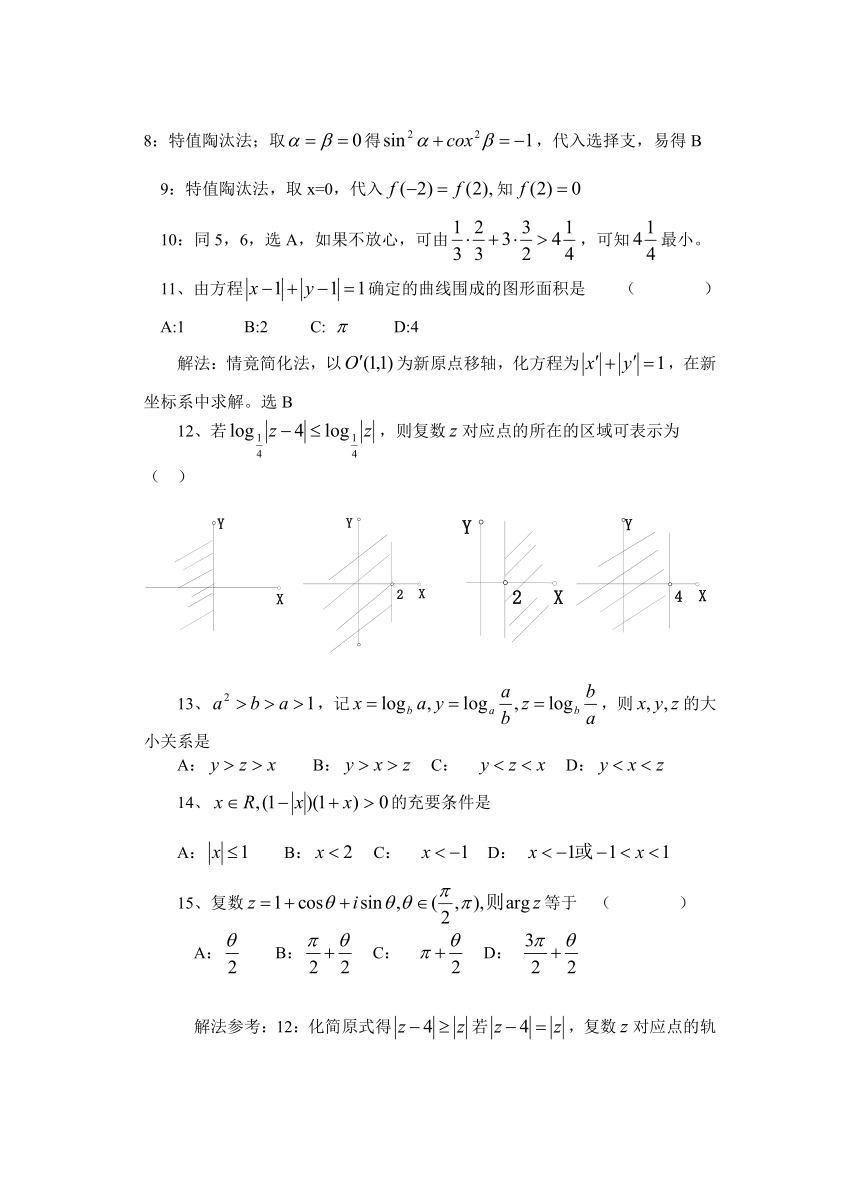
12、若，则复数对应点的所在的区域可表示为　（　）
　　　　　　　　　　　　　　　　　　　　　　　　
13、，记，则的大小关系是
A：　　B：　C：　　D：
14、的充要条件是　　　　　　　　
A：　　B：　C：　　D：
15、复数等于　（　　　　）
　A：　　B：　C：　　D：
解法参考：12：化简原式得若，复数对应点的轨迹是x＝2，故表示含有直线经＝2的半个平面。又满足不等式，故知选B。　这里应用了先简再作局部检验的方法。
13、特值陶汰法，取，可选C
14、特值检验法，取x＝－1可去A，B，取x＝0可去C，得D
15、局部检验法，注意到故复数对点第一象限， 选A
16：若　　　（　　　）
A：　　B：　C：　　D：
17：在等差数列中，　　　（　　　）
A：　　B：　C：　　D：
18:首项等于1，公比为的等比数列，前项和等于，那么这个数列的前项的倒数的和等于　　　　　　　　　　　　　　　　　（　　　　）
A：　　B：　C：　　D：
19：设
A：　　B：　C：　　D：
解法参考：
16：由的对应点在第二象限，且同法可判断所以，选D
17、特例：，选D
18、令考虑到选择支的唯一性，选D
19、汪意到，故，选A
题目：
21、若( )
A: B：　C：　D：
22、已知　　　　（　　　　　）
A： B：　C：　D：
23、可化简为　　　　　　　　　（　　）
A： B：　C：　D：
24、函数的图像如图，则（　）
A： 　　　　B：　　　　　　　C：　　　　　D：
25、函数的值域是　　（　　　）
A： B： 　
C：　D：
解法参考：
21：特值检验法：取，去掉B，D，取则选C
22：取满足已知条件，则选C
23：由，而不存在，去掉A，D
由原式有意义，而不存在，去掉C，选B
24：显然，周期排除A，B，再考虑图像可由
的图像左右平移而得，选C
25：注意选项差异，注意，选B
习题26：的图像关于直线对称，则a=
A：　　B：　　C：　　　D：
27、函数是（　　　　）
A：　 　B：　 　C：　　　 D：
28、是第二象限角，则必有　（　　　　）
A：　　B：　　C：　　　
D：
29、，那么函数的最小值是　（　　　）
A：　　B：　　C：　　　D：
30、圆锥轴截面顶角为，则它的侧面展开图的扇形圆心角等于（　　）
A：　　B：　　C：　　　D：
解题参考：
26：代入检验法。法二：注意对称性，由,选D
27：函数图像上的点对称的点是它本身，而选B
28、，令，选A
29、显然可取负值，（
则，这在已知条件中是不可能的，故，去B，C，选D
30、易知，当，选D，这里应用了根限观点。
题目：31、设过长方体同一顶点的三个面的对角线分别是那么这个长方体的对角线长是 ( )
A:　　　　　　　　　 B：　
C：　　　　　　　D：
32、使成立的的取值范围是　　　　（　　　）
A：　B：　　C：　　D：
33、已知上是减函数，则的取值范围是　（　）
A：　B：　C：　　D：
34：若的取值范围是　　（　　　　）
A：　B：　C：　　D：
35、的最大值是　　　　　　　　　　　（　　　）
A：　B：　C：　　D：
解法参考：
31：如图，设长宽高分别为令则
此是只有
B式，选B
32、x=1满足原不等式，选B
33、由，去C　，　（否则当x=1时真数为0）去D
由，函数在是增函数，去A，选B
34：满足轮换对称，所求范围也应是对称的，选B
35、表示圆上的点与原点连线的斜率，选D
题目　：36、设是复数，，则
A：　B：　C：　D：
37、已知过球面上三点的截面和球心的距离等于球半径的一半，且，则球的表面积是　　　　　　（　　　　）
A：　　　B：　C：　　　　D：
38、数列的前项和为　　　　　（　　　　）
A：　　　　　　B： 　　　　　　C：　　　　　　　　　　D：
39、奇函数的定义域是，单调递减，
且，则的取值范围是　　（　　　　　）
A：　　　　　　　B：　　　　　　　　
C：　　　　　　　　D：
40、设点，的右焦点，点在椭圆上移动，当取最小值时点的坐标是　　　　（　　　）
A：　B：　C：　　D：
解法参考：
36、几何法：利用复数加法，减法的几何意义作图，点D对应复数，点对应复数，点对应复数，向量对应复数，向量，据已知，故平行四边形是菱形，因而的模为2，辐角主值为，，选D
37、变换简化。转化为求球半径，若球半径为，等边的外接圆半径为，由，选D
38、特值检验法，当n=1立得（C）
39、由，又由得，去（C），选B
40、几何法解题，过点M作（为在准线）则于是问题转化为求取最小值时的点M的坐标。显然当共线时取最小值。这时M在第一象限，选（C）
最后总结一下，在以上解题方法的介绍中，我们所提及的都是间接解法，这不意味着直接解法不可取，只是在在一般情况下，直接解法都比较机械，计算复杂，费劲等，因此往往实用性稍差。一种好的间接方法往往灵巧，快速，但应当承认直接法和间接法中常常具有良好的互补性。有许多间接法也正是由直接计算得到的启示的。如下例：
已知　
解法：由
，选A试
试想在求的程中，由进而利用万能公式可解方程求得最终也可由的范围进行取舍。　可见直接法和间接法的关系还是非常密切的。当然无论是直接法还是间接法解选择题都需要我们有扎实的基本功。而间接法更要求能对题设，选项蕴含的数学信息进行充分的挖掘与利用。解题时需要具备良好的思维策略，敏锐洞察力，更需要灵感，选择最佳方案。一个好的解题方案实际上是一种智慧的闪光，探索最佳方案也是对智慧的挑战。另外解选择题的种种方法对于其他题型，特别是填空题，具有良好的移植，借鉴，辐射作用，这里的对于某种数学环境下的种种判断，对于分析解决更为复杂的数学问题往往也很有帮助。重视选择解法在似乎无章可循中寻找有章可循。