单元复习25 概率初步 复习课件(共24张PPT)
文档属性
| 名称 | 单元复习25 概率初步 复习课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
人教版九年级上册
单元 25
概率初步
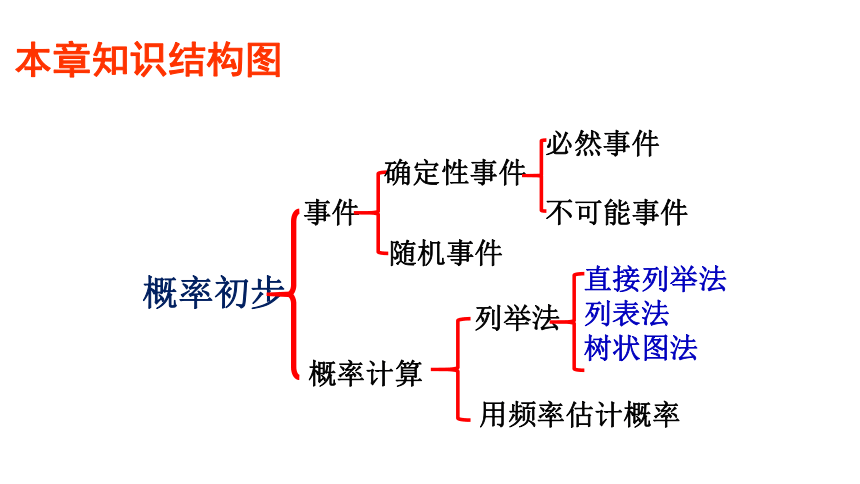
概率初步
事件
确定性事件
随机事件
必然事件
不可能事件
概率计算
列举法
用频率估计概率
直接列举法
列表法
树状图法
本章知识结构图
一、事件的分类及其概念
事件
确定事件
随机事件
必然事件
不可能事件
1.在一定条件下必然发生的事件,叫做必然事件;
2.在一定条件下不可能发生的事件,叫做不可能事件;
3.在一定条件下可能发生也可能不发生的事件,叫做随
机事件.
知识点梳理
1.概率: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A).
二、概率的概念
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
2.
三、随机事件的概率的求法
1.①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件
可能性的大小,但频率具有随机性,概率是自身固有
的性质,不具有随机性.
2.概率的计算公式:
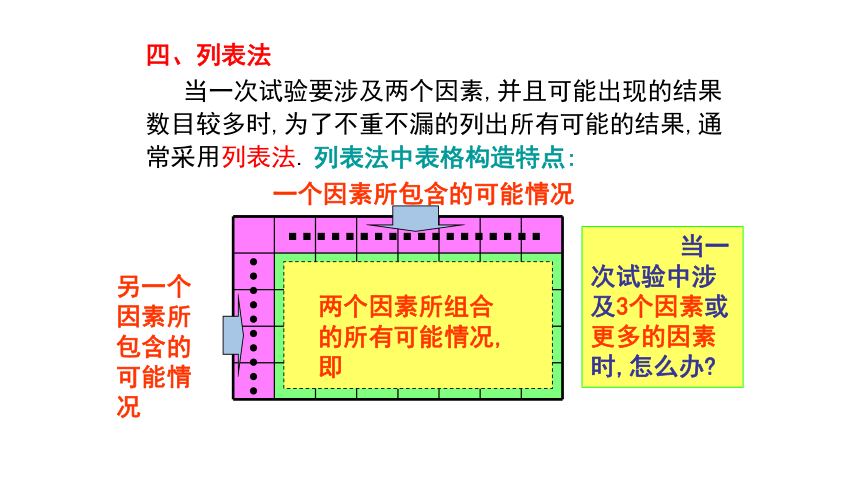
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办
四、列表法
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
五、树状图法
知识点一 判断事件类型
1.下列事件中,是必然事件的是( )
A.掷一次骰子,向上一面的点数是6
B.13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月
C.射击运动员射击一次,命中靶心
D.经过有交通信号灯的路口,遇到红灯
B
知识点专题训练
2.(福建中考)投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
D
C
C
8.一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为;
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
知识点三 用频率估计概率
9.某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
D
10.(2019·白银)一个猜想是否正确,科学家们要经过反复的实验论证.下表是几位科学家“掷硬币”的实验数据:
请根据以上数据,估计硬币出现“正面朝上”的概率为________ (精确到0.1).
0.5
20
1.投掷两枚质地均匀的骰子,骰子的六个面上分别刻
有1到6的点数,则下列事件为随机事件的是
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
D
本章综合练习
2.(2018·孝感)下列说法正确的是
A.了解“孝感市初中生每天课外阅读书籍时间的情况”
最适合的调查方式是全面调查
B.甲乙两人跳绳各10次,其成绩的平均数相等,s甲2>s乙2,
则甲的成绩比乙稳定
C.三张分别画有菱形、等边三角形、圆的卡片,从中随机抽取一张,
恰好抽到中心对称图形卡片的概率是
D.“任意画一个三角形,其内角和是360°”这一事件是不可能事件
D
D
B
5.(2018·绥化)如图,一块飞镖游戏板由大小相等的小正方形格子构成,
向游戏板随机投掷一枚飞镖,击中黑色区域的概率是_____.
6.(2018·内江)有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中抽取一张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是_____.
8.将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其他方面完全相同,若背面向上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,
写出(x,y)所有可能出现的结果;
(2)求取出的两张卡片上的数字之和为偶数的概率P.
解:(1)画树状图得:
由树状图知共有6种等可能的结果:
(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)
人教版九年级上册
单元 25
概率初步
概率初步
事件
确定性事件
随机事件
必然事件
不可能事件
概率计算
列举法
用频率估计概率
直接列举法
列表法
树状图法
本章知识结构图
一、事件的分类及其概念
事件
确定事件
随机事件
必然事件
不可能事件
1.在一定条件下必然发生的事件,叫做必然事件;
2.在一定条件下不可能发生的事件,叫做不可能事件;
3.在一定条件下可能发生也可能不发生的事件,叫做随
机事件.
知识点梳理
1.概率: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A).
二、概率的概念
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
2.
三、随机事件的概率的求法
1.①当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时,我们用大量重复试验中随机事件发生的稳定频率来估计概率.
②频率与概率的关系:两者都能定量地反映随机事件
可能性的大小,但频率具有随机性,概率是自身固有
的性质,不具有随机性.
2.概率的计算公式:
当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即
列表法中表格构造特点:
当一次试验中涉及3个因素或更多的因素时,怎么办
四、列表法
当一次试验中涉及2个因素或更多的因素时, 为了不重不漏地列出所有可能的结果,通常采用“树状图”.
树形图的画法:
一个试验
第一个因数
第二个
第三个
如一个试验中涉及2个或3个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况;第三个因数中有2种可能的情况.
A
B
1
2
3
1
2
3
a
b
a
b
a
b
a
b
a
b
a
b
n=2×3×2=12
五、树状图法
知识点一 判断事件类型
1.下列事件中,是必然事件的是( )
A.掷一次骰子,向上一面的点数是6
B.13个同学参加一个聚会,他们中至少有两个同学的生日在同一个月
C.射击运动员射击一次,命中靶心
D.经过有交通信号灯的路口,遇到红灯
B
知识点专题训练
2.(福建中考)投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
D
C
C
8.一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为;
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
知识点三 用频率估计概率
9.某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
D
10.(2019·白银)一个猜想是否正确,科学家们要经过反复的实验论证.下表是几位科学家“掷硬币”的实验数据:
请根据以上数据,估计硬币出现“正面朝上”的概率为________ (精确到0.1).
0.5
20
1.投掷两枚质地均匀的骰子,骰子的六个面上分别刻
有1到6的点数,则下列事件为随机事件的是
A.两枚骰子向上一面的点数之和大于1
B.两枚骰子向上一面的点数之和等于1
C.两枚骰子向上一面的点数之和大于12
D.两枚骰子向上一面的点数之和等于12
D
本章综合练习
2.(2018·孝感)下列说法正确的是
A.了解“孝感市初中生每天课外阅读书籍时间的情况”
最适合的调查方式是全面调查
B.甲乙两人跳绳各10次,其成绩的平均数相等,s甲2>s乙2,
则甲的成绩比乙稳定
C.三张分别画有菱形、等边三角形、圆的卡片,从中随机抽取一张,
恰好抽到中心对称图形卡片的概率是
D.“任意画一个三角形,其内角和是360°”这一事件是不可能事件
D
D
B
5.(2018·绥化)如图,一块飞镖游戏板由大小相等的小正方形格子构成,
向游戏板随机投掷一枚飞镖,击中黑色区域的概率是_____.
6.(2018·内江)有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中抽取一张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是_____.
8.将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其他方面完全相同,若背面向上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面向上放在桌面上,从中先随机抽取一张卡片,记该卡片上的数字为x,再把剩下的两张卡片洗匀后,背面向上放在桌面上,再从这两张卡片中随机抽取一张卡片,记该卡片上的数字为y.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,
写出(x,y)所有可能出现的结果;
(2)求取出的两张卡片上的数字之和为偶数的概率P.
解:(1)画树状图得:
由树状图知共有6种等可能的结果:
(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)
同课章节目录
