6.2实数(3) 课件(共25张PPT)
图片预览







文档简介
(共25张PPT)
沪科版七年级下册
6.2 实数(3)
教学目标
1.了解实数与数轴上的点具有一一对应的关系.
2.了解实数的相反数,绝对值,倒数的意义.
教学重点:
实数的相反数,绝对值,倒数的意义.
教学难点:
理解实数与数轴上的点具有一一对应的关系.
新知导入
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的
无理数的点吗?
π和
2
新知讲解
0
1
2
4
3
-1
-2
π
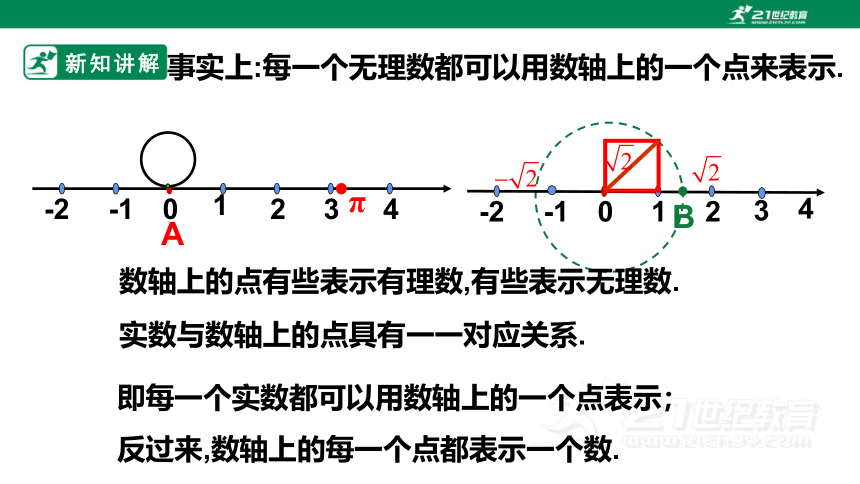
如图,把直径等于1的圆放在数轴上,圆上一点A与表示0的点重合,圆沿着数数轴正方向滚动一周,
A
π.
此时点A表示的数就是无理数
如图, 在数轴上,以原点为正方形的一个顶点,单位长度1为边长作一个正方形,再以原点为圆心,正方形的对角线为半径画弧,弧与数轴正方向交于点B.
此时点B表示的数就是无理数 .
新知讲解
0
1
2
4
3
-1
-2
B
新知讲解
0
1
2
4
3
-1
-2
B
0
1
2
4
3
-1
-2
π
A
事实上:每一个无理数都可以用数轴上的一个点来表示.
数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点具有一一对应关系.
即每一个实数都可以用数轴上的一个点表示;
反过来,数轴上的每一个点都表示一个数.
例题解析
如图, 数轴上,表示实数 的点是 .
15
A
2
3
4
1
0
B
C
D
实数与数轴上的点是一一对应关 系,要想知道数轴上表示实数 的点的位置,只要知道 在哪两个相邻整数之间,再对比所给数轴上已知点的位置,即得解.
解析:
15
15
∵32<15<42,
∴ 是介于3和4之间的数,
15
并且 与4的距离要近一些.
15
∴答案为 C.
C
课堂练习
1. 如图, 数轴上,表示 的点是 .
3
A
0
1
2
4
3
-1
-2
-3
-4
5
B
C
B
M
0
1
2
4
3
-1
-2
-3
-4
5
2. 如图, 数轴上, 点M表示的数可能是( ).
A. ; B. - ; C. ; D. - .
3
3
7
7
D
例题解析
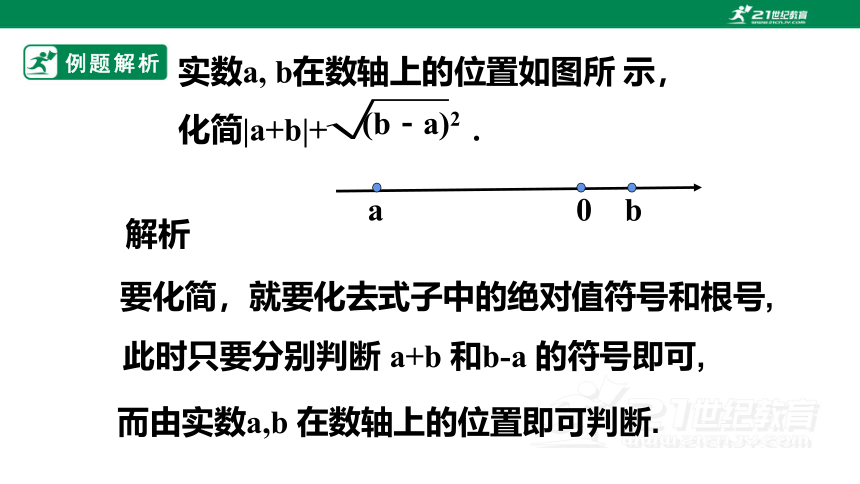
实数a, b在数轴上的位置如图所 示,
化简|a+b|+ .
(b-a)2
0
b
a
要化简,就要化去式子中的绝对值符号和根号,
解析
此时只要分别判断 a+b 和b-a 的符号即可,
而由实数a,b 在数轴上的位置即可判断.
例题解析
实数a, b在数轴上的位置如图所 示,
化简|a+b|+ .
(b-a)2
0
b
a
由实数a,b在数轴上的位置,可知
+(b-a)
-(a+b)
= - 2a
(b-a)2
解这类借助数轴化简或求值的问题时, 关键是通过某些点在数轴上的位置判断绝对值符号及根号内式子的符号,进而化去绝对值符号和根号.
解:
a<0,b>0,且|a|>|b|.
∴a+b<0,b-a>0.
∴|a+b|+ =
课堂练习
1.实数a在数轴上的位置如图所示,则|a - 1|= .
0
1
-1
a
1-a
2.如图,在数轴上表示2, 的对应点分别为 C,B,
点C是AB的中点,则点A表示的数是 .
7
1
2
0
3
A
C
B
7
-
4
7
新知讲解
有理数关于相反数,绝对值和倒数的意义是什么?
在实数范围内,相反数,绝对值,倒数的意义和有理数范围内的相反数,绝对值的意义完全一样.
实数 a 的相反数是 - a ,
一个正实数a的绝对值是它本身;
一个负实数a的绝对值是它的相反数;
0的绝对值是0.
| a |
=a,
= -a.
| a |
实数 a 的倒数是 (a ≠ 0).
1
a
讲解新知
你能解答下列问题吗
(1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .
0
0
例题解析
例
(1)分别写出 的相反数;
(2)指出 是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
例题解析
解:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是 .
(4) 绝对值是 的数是 或 .
4
2.5的绝对值是 ;
- 的绝对值是 ;
- 的绝对值是 ;
的绝对值是 .
0的绝对值是 .
解: 2.5的相反数是 ;
- 的相反数是 ;
- 的相反数是 ;
的相反数是 ;
0的相反数是 .
课堂练习
求下列各数的相反数与绝对值:
π
2
- 2.5
π
2
π
2
π
2
2.5
7
7
7
7
3
2
-
3
2
-
3
2
-
2
3
-
0
0
例题解析
已知a是最大的负整数, b是 的小数部分,
c是 的相反数, d没有倒数. 试求 的值.
先根据题意,确定a,b,c,d的值,再 代入算式计算.
解析
∴b= -2
∵ a是最大的负整数,
∴a= - 1,
∴d=0.
∵ b是 的小数部分,
∵ d没有倒数.
解:
7
6
7
7
∵ c是 的相反数,
6
∴c= -
6
| a-b|-
1
2
cd
∴
| a-b|-
1
2
cd
=
1
2
×(- )×0
6
| -1-( - 2)|
7
=| 1- |
7
7
1
-
=
-
课堂练习
已知a,b,c,d均为实数,且a,b互为相反数,c,d互为倒数,m 的算术平方根等于它本身,p是平方根等于本身的实数.求 p2023 +cd+ +m 的值..
a+b
π
解:
∵ a,b互为相反数,
∴a+b=0.
∵ c,d互为倒数,
∴cd=1.
∵ m 的算术平方根等于它本身,
∴m=1或m=0.
∵ p是平方根等于本身的实数,
∴p=0.
课堂练习
解:
∵ a,b互为相反数,
∴a+b=0.
∵ c,d互为倒数,
∴cd=1.
∵ m 的算术平方根等于它本身,
∴m=1或m=0.
∵ p是平方根等于本身的实数,
∴p=0.
当m=1时,
当m=0时,
a+b
π
p2023 +cd+ +m
=02023 +1+ +1
π
0
=2
a+b
π
p2023 +cd+ +m
=02023 +1+ +0
π
0
=1
a+b
π
p2023 +cd+ +m
∴
的值为2或1.
课堂小结
1.实数与数轴上的点具有怎样的关系.
2.如何求一个实数的相反数,绝对值,倒数?.
巩固新知
1.实数 - 的绝对值是( ).
2
A. ; B. - ; C. ; D. .
2
2
2
2
2
2.化简 的结果是( ).
| 3 -π |- π
A. ; B. - ; C. ; D. .
3
3
3 -2π
2π-3
C
B
巩固新知
3.实数 - 的相反数是 ;
绝对值是 ;倒数是 .
2
4.如图,若将三个数- , , 表示在数轴上,
其中被阴影覆盖的数是 .
3
-
3
2
-
3
2
1
-
2
3
5
8
11
0
1
2
4
3
-1
-2
-3
-4
5
11
作业布置
今天作业
课本P16页第2、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版七年级下册
6.2 实数(3)
教学目标
1.了解实数与数轴上的点具有一一对应的关系.
2.了解实数的相反数,绝对值,倒数的意义.
教学重点:
实数的相反数,绝对值,倒数的意义.
教学难点:
理解实数与数轴上的点具有一一对应的关系.
新知导入
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的
无理数的点吗?
π和
2
新知讲解
0
1
2
4
3
-1
-2
π
如图,把直径等于1的圆放在数轴上,圆上一点A与表示0的点重合,圆沿着数数轴正方向滚动一周,
A
π.
此时点A表示的数就是无理数
如图, 在数轴上,以原点为正方形的一个顶点,单位长度1为边长作一个正方形,再以原点为圆心,正方形的对角线为半径画弧,弧与数轴正方向交于点B.
此时点B表示的数就是无理数 .
新知讲解
0
1
2
4
3
-1
-2
B
新知讲解
0
1
2
4
3
-1
-2
B
0
1
2
4
3
-1
-2
π
A
事实上:每一个无理数都可以用数轴上的一个点来表示.
数轴上的点有些表示有理数,有些表示无理数.
实数与数轴上的点具有一一对应关系.
即每一个实数都可以用数轴上的一个点表示;
反过来,数轴上的每一个点都表示一个数.
例题解析
如图, 数轴上,表示实数 的点是 .
15
A
2
3
4
1
0
B
C
D
实数与数轴上的点是一一对应关 系,要想知道数轴上表示实数 的点的位置,只要知道 在哪两个相邻整数之间,再对比所给数轴上已知点的位置,即得解.
解析:
15
15
∵32<15<42,
∴ 是介于3和4之间的数,
15
并且 与4的距离要近一些.
15
∴答案为 C.
C
课堂练习
1. 如图, 数轴上,表示 的点是 .
3
A
0
1
2
4
3
-1
-2
-3
-4
5
B
C
B
M
0
1
2
4
3
-1
-2
-3
-4
5
2. 如图, 数轴上, 点M表示的数可能是( ).
A. ; B. - ; C. ; D. - .
3
3
7
7
D
例题解析
实数a, b在数轴上的位置如图所 示,
化简|a+b|+ .
(b-a)2
0
b
a
要化简,就要化去式子中的绝对值符号和根号,
解析
此时只要分别判断 a+b 和b-a 的符号即可,
而由实数a,b 在数轴上的位置即可判断.
例题解析
实数a, b在数轴上的位置如图所 示,
化简|a+b|+ .
(b-a)2
0
b
a
由实数a,b在数轴上的位置,可知
+(b-a)
-(a+b)
= - 2a
(b-a)2
解这类借助数轴化简或求值的问题时, 关键是通过某些点在数轴上的位置判断绝对值符号及根号内式子的符号,进而化去绝对值符号和根号.
解:
a<0,b>0,且|a|>|b|.
∴a+b<0,b-a>0.
∴|a+b|+ =
课堂练习
1.实数a在数轴上的位置如图所示,则|a - 1|= .
0
1
-1
a
1-a
2.如图,在数轴上表示2, 的对应点分别为 C,B,
点C是AB的中点,则点A表示的数是 .
7
1
2
0
3
A
C
B
7
-
4
7
新知讲解
有理数关于相反数,绝对值和倒数的意义是什么?
在实数范围内,相反数,绝对值,倒数的意义和有理数范围内的相反数,绝对值的意义完全一样.
实数 a 的相反数是 - a ,
一个正实数a的绝对值是它本身;
一个负实数a的绝对值是它的相反数;
0的绝对值是0.
| a |
=a,
= -a.
| a |
实数 a 的倒数是 (a ≠ 0).
1
a
讲解新知
你能解答下列问题吗
(1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .
0
0
例题解析
例
(1)分别写出 的相反数;
(2)指出 是什么数的相反数;
(3)求 的绝对值;
(4)已知一个数的绝对值是 ,求这个数.
例题解析
解:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是 .
(4) 绝对值是 的数是 或 .
4
2.5的绝对值是 ;
- 的绝对值是 ;
- 的绝对值是 ;
的绝对值是 .
0的绝对值是 .
解: 2.5的相反数是 ;
- 的相反数是 ;
- 的相反数是 ;
的相反数是 ;
0的相反数是 .
课堂练习
求下列各数的相反数与绝对值:
π
2
- 2.5
π
2
π
2
π
2
2.5
7
7
7
7
3
2
-
3
2
-
3
2
-
2
3
-
0
0
例题解析
已知a是最大的负整数, b是 的小数部分,
c是 的相反数, d没有倒数. 试求 的值.
先根据题意,确定a,b,c,d的值,再 代入算式计算.
解析
∴b= -2
∵ a是最大的负整数,
∴a= - 1,
∴d=0.
∵ b是 的小数部分,
∵ d没有倒数.
解:
7
6
7
7
∵ c是 的相反数,
6
∴c= -
6
| a-b|-
1
2
cd
∴
| a-b|-
1
2
cd
=
1
2
×(- )×0
6
| -1-( - 2)|
7
=| 1- |
7
7
1
-
=
-
课堂练习
已知a,b,c,d均为实数,且a,b互为相反数,c,d互为倒数,m 的算术平方根等于它本身,p是平方根等于本身的实数.求 p2023 +cd+ +m 的值..
a+b
π
解:
∵ a,b互为相反数,
∴a+b=0.
∵ c,d互为倒数,
∴cd=1.
∵ m 的算术平方根等于它本身,
∴m=1或m=0.
∵ p是平方根等于本身的实数,
∴p=0.
课堂练习
解:
∵ a,b互为相反数,
∴a+b=0.
∵ c,d互为倒数,
∴cd=1.
∵ m 的算术平方根等于它本身,
∴m=1或m=0.
∵ p是平方根等于本身的实数,
∴p=0.
当m=1时,
当m=0时,
a+b
π
p2023 +cd+ +m
=02023 +1+ +1
π
0
=2
a+b
π
p2023 +cd+ +m
=02023 +1+ +0
π
0
=1
a+b
π
p2023 +cd+ +m
∴
的值为2或1.
课堂小结
1.实数与数轴上的点具有怎样的关系.
2.如何求一个实数的相反数,绝对值,倒数?.
巩固新知
1.实数 - 的绝对值是( ).
2
A. ; B. - ; C. ; D. .
2
2
2
2
2
2.化简 的结果是( ).
| 3 -π |- π
A. ; B. - ; C. ; D. .
3
3
3 -2π
2π-3
C
B
巩固新知
3.实数 - 的相反数是 ;
绝对值是 ;倒数是 .
2
4.如图,若将三个数- , , 表示在数轴上,
其中被阴影覆盖的数是 .
3
-
3
2
-
3
2
1
-
2
3
5
8
11
0
1
2
4
3
-1
-2
-3
-4
5
11
作业布置
今天作业
课本P16页第2、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
