6.2实数(1) 课件(共25张PPT)
图片预览





文档简介
(共25张PPT)
6.2 实数(1)
沪科版七年级下册
教学目标
1.了解无理数和实数的意义.
2.能对实数按要求进行分类.
教学重点:无理数和实数的概念.
教学难点:无理数和实数的概念.
新知导入
如图是由4条横线,5条竖线构成的方格网,它们相邻的行距,列距都是1.从这些纵横线相交得出20个点称为格点,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.你能找出多少种面积互不相同的格点正方形?
新知讲解
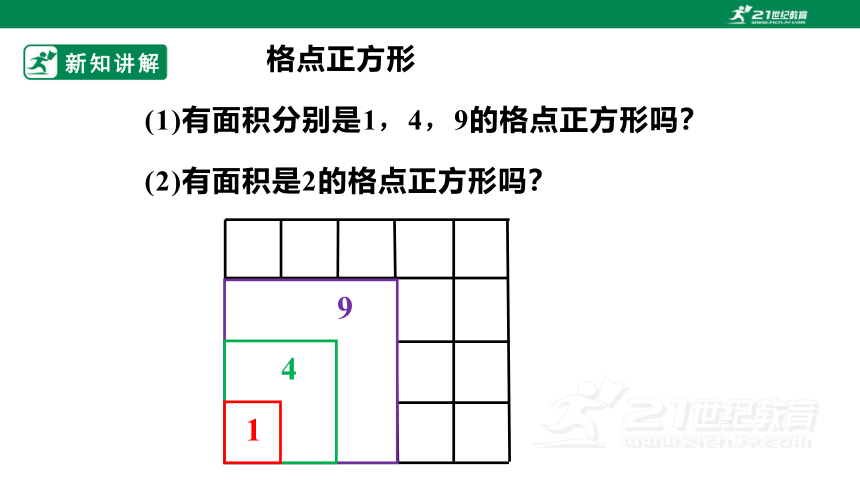
格点正方形
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?
1
4
9
新知讲解
格点正方形.
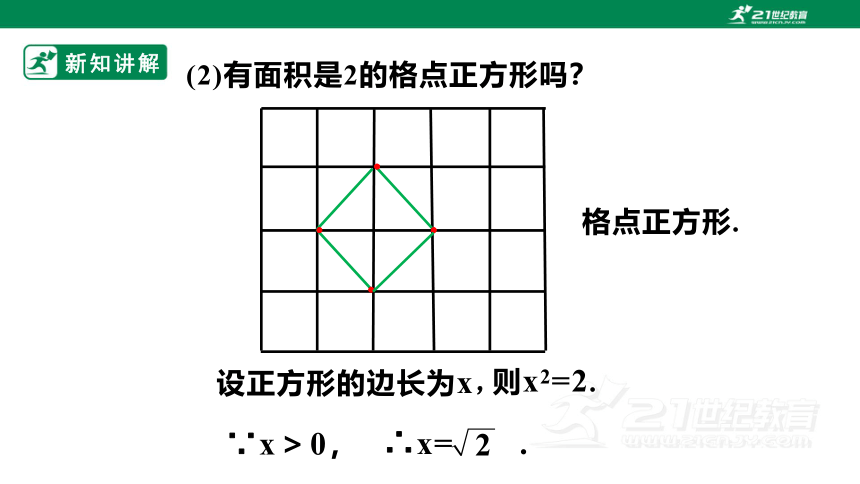
(2)有面积是2的格点正方形吗?
设正方形的边长为x,
∵x>0,
∴x= .
2
则x2=2.
新知讲解
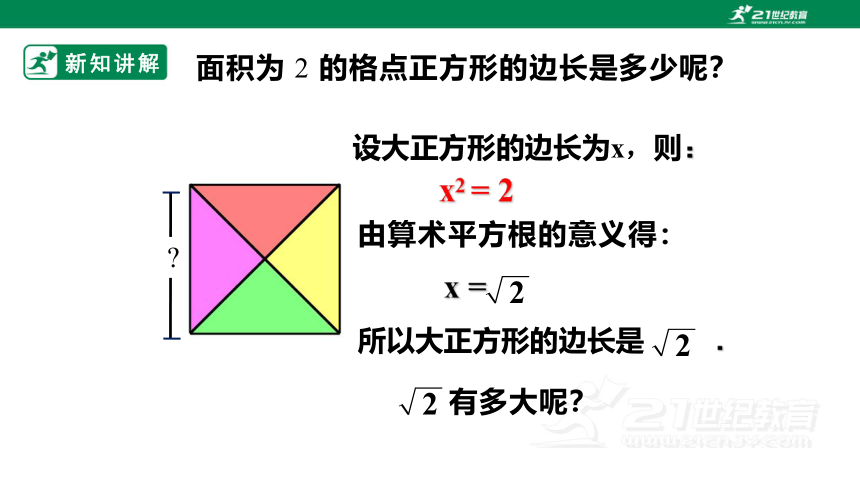
面积为 2 的格点正方形的边长是多少呢?
设大正方形的边长为x,则:
由算术平方根的意义得:
所以大正方形的边长是 .
x2 = 2
x =
2
2
有多大呢?
2
新知讲解
∵ 1<2<4,
∴
<
<
1
2
4
有多大呢?
2
你能不能得到 的更精确的取值?
2
的大小在1和2之间.
2
2
1
<
<
2
∴
新知讲解
有多大呢?
……
∵
∵
∵
∴
∴
∴
新知讲解
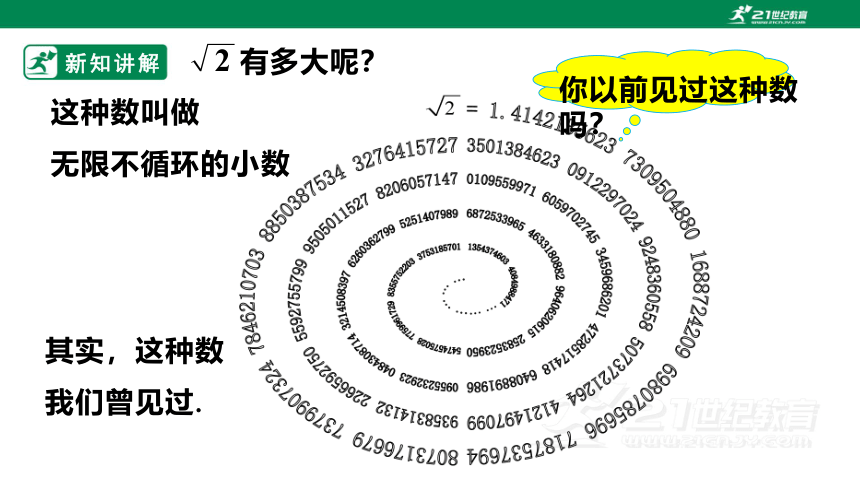
你以前见过这种数吗?
这种数叫做
无限不循环的小数
有多大呢?
2
其实,这种数
我们曾见过.
新知讲解
无限不循环的小数
现代的计算机计算到22万亿位,
没有除尽,也没有发现循环,
22万亿=2.2×1013
1.4亿本数学书的文字
=3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 ……
π
新知讲解
0.101001000100001000001…[两个1之间依次多1个0]
无限不循环的小数
-168.323223222322223…[两个3之间依次多1个2]
无限不循环的小数和我们以前学习过的有理数有什么不同?
我们怎样定义这种新数?
我们先来观察一下有理数化为小数时,它的形式是怎样的?
新知讲解
有理数包括整数和分数,如果将下列有理数写成小数的形式,你有什么发现?
新知讲解
反过来,任何有限小数或无限循环小数也都是有理数.
任何一个有理数都可以写成有限小数或无限循环小数.
有理数
有限小数
无限循环小数
新知讲解
0.101001000100001000001…[两个1之间依次多1个0]
这些是无限不循环小数,
2
=1.4142135623……
π =3.141592653589……
象
显然不符合有理数的定义.
我们叫它做无理数.
新知讲解
无限不循环的小数叫做无理数.
0.2020020002…[两个2之间依次多1个0]
-2023.3131131113…[两个3之间依次多1个1]
3
3 ,
3
9 ,
1.
2
+
π
无理数的定义
(1)开不尽方的数
(2)圆周率 π及一些含有 π的数
(3)有一定的规律,但不循环的无限小数
呈现无理数的三种形式:
π
2
- ,
2π,
2 ,
5 ,
12 ,
-
如:
课堂练习
你能举出一些无理数吗?
(1)开不尽方类
(2)含有 π的数
(3)有一定的规律,但不循环的无限小数
3
16 ,
7 ,
21 ,
-
1.
2
-
π
2π
3
- ,
4π,
0.8080080008…[两个8之间依次多1个0]
-5.6161161116…[两个6之间依次多1个1]
数学花絮
毕达哥拉斯斯学派认为“万物皆数(整数)”一切数均可表成整数或整数之比” 然而有一天,本学派的希帕索斯发现:边长为1的正方形其对角线长度是多少呢?
他发现这一长度既不能用整数,也不能用分数表示,而只能用一个新数来表示.希帕索斯的发现导致了数学史上第一个无理数的诞生.
讲解新知
实数
有理数
无理数
正有理数
负有理数
无限不循环小数
0
正无理数
负无理数
有限小数或
无限循环小数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
实数的分类
实数的定义
有理数和无理数统称实数.
对应训练
把下列各数填入相应的集合内:
0,1,3,-1,-2, , ,0.4,-0.25,
1
3
1
2
-
3.14,π, , , , , , .
3
2
3
64
10
-
8
3
-
2
2
有理数
无理数
0,
1,
3,
-1,
-2,
1
2
-
,
1
3
,
0.4,
-0.25,
3.14,
8
3
-
π,
3
,
2
3
,
10
-
,
2
2
.
64
,
1.下列说法中,正确的是 ( ).
课堂练习
A.无理数都是无限小数; B.无理数都是开方开不尽的数;
C.带根号的都是无理数; D.无限小数都是无理数.
A
2.对于数 ,下列说法中正确的是( ).
3
-
2
A.它是有理数; B.它是整数;
C.它是分数; D.它是无理数.
D
课堂练习
3.下列实数中:-1.414, , , , , , ,
0.1010010001,其中无理数的个数有 ( ).
22
7
π
2
-
-8
3
25
7
2
3
A.2个; B.3个; C.4个; D.5个.
B
4.下列说法中,正确的是 ( ).
A.实数分为正实数和负实数; B.不带根号的数都是有理数;
C. 无理数包括正无理数和负无理数; D.无理数不是实数.
C
课堂总结
1.什么样的数叫做无理数?试举出几个无理数的例子.
2.什么样的数叫做实数?你会对实数进行分类码?
作业布置
今天作业
课本P15页第1、2 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.2 实数(1)
沪科版七年级下册
教学目标
1.了解无理数和实数的意义.
2.能对实数按要求进行分类.
教学重点:无理数和实数的概念.
教学难点:无理数和实数的概念.
新知导入
如图是由4条横线,5条竖线构成的方格网,它们相邻的行距,列距都是1.从这些纵横线相交得出20个点称为格点,我们可以选择其中4个格点作为顶点连接成一个正方形,叫做格点正方形.你能找出多少种面积互不相同的格点正方形?
新知讲解
格点正方形
(1)有面积分别是1,4,9的格点正方形吗?
(2)有面积是2的格点正方形吗?
1
4
9
新知讲解
格点正方形.
(2)有面积是2的格点正方形吗?
设正方形的边长为x,
∵x>0,
∴x= .
2
则x2=2.
新知讲解
面积为 2 的格点正方形的边长是多少呢?
设大正方形的边长为x,则:
由算术平方根的意义得:
所以大正方形的边长是 .
x2 = 2
x =
2
2
有多大呢?
2
新知讲解
∵ 1<2<4,
∴
<
<
1
2
4
有多大呢?
2
你能不能得到 的更精确的取值?
2
的大小在1和2之间.
2
2
1
<
<
2
∴
新知讲解
有多大呢?
……
∵
∵
∵
∴
∴
∴
新知讲解
你以前见过这种数吗?
这种数叫做
无限不循环的小数
有多大呢?
2
其实,这种数
我们曾见过.
新知讲解
无限不循环的小数
现代的计算机计算到22万亿位,
没有除尽,也没有发现循环,
22万亿=2.2×1013
1.4亿本数学书的文字
=3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 ……
π
新知讲解
0.101001000100001000001…[两个1之间依次多1个0]
无限不循环的小数
-168.323223222322223…[两个3之间依次多1个2]
无限不循环的小数和我们以前学习过的有理数有什么不同?
我们怎样定义这种新数?
我们先来观察一下有理数化为小数时,它的形式是怎样的?
新知讲解
有理数包括整数和分数,如果将下列有理数写成小数的形式,你有什么发现?
新知讲解
反过来,任何有限小数或无限循环小数也都是有理数.
任何一个有理数都可以写成有限小数或无限循环小数.
有理数
有限小数
无限循环小数
新知讲解
0.101001000100001000001…[两个1之间依次多1个0]
这些是无限不循环小数,
2
=1.4142135623……
π =3.141592653589……
象
显然不符合有理数的定义.
我们叫它做无理数.
新知讲解
无限不循环的小数叫做无理数.
0.2020020002…[两个2之间依次多1个0]
-2023.3131131113…[两个3之间依次多1个1]
3
3 ,
3
9 ,
1.
2
+
π
无理数的定义
(1)开不尽方的数
(2)圆周率 π及一些含有 π的数
(3)有一定的规律,但不循环的无限小数
呈现无理数的三种形式:
π
2
- ,
2π,
2 ,
5 ,
12 ,
-
如:
课堂练习
你能举出一些无理数吗?
(1)开不尽方类
(2)含有 π的数
(3)有一定的规律,但不循环的无限小数
3
16 ,
7 ,
21 ,
-
1.
2
-
π
2π
3
- ,
4π,
0.8080080008…[两个8之间依次多1个0]
-5.6161161116…[两个6之间依次多1个1]
数学花絮
毕达哥拉斯斯学派认为“万物皆数(整数)”一切数均可表成整数或整数之比” 然而有一天,本学派的希帕索斯发现:边长为1的正方形其对角线长度是多少呢?
他发现这一长度既不能用整数,也不能用分数表示,而只能用一个新数来表示.希帕索斯的发现导致了数学史上第一个无理数的诞生.
讲解新知
实数
有理数
无理数
正有理数
负有理数
无限不循环小数
0
正无理数
负无理数
有限小数或
无限循环小数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
实数的分类
实数的定义
有理数和无理数统称实数.
对应训练
把下列各数填入相应的集合内:
0,1,3,-1,-2, , ,0.4,-0.25,
1
3
1
2
-
3.14,π, , , , , , .
3
2
3
64
10
-
8
3
-
2
2
有理数
无理数
0,
1,
3,
-1,
-2,
1
2
-
,
1
3
,
0.4,
-0.25,
3.14,
8
3
-
π,
3
,
2
3
,
10
-
,
2
2
.
64
,
1.下列说法中,正确的是 ( ).
课堂练习
A.无理数都是无限小数; B.无理数都是开方开不尽的数;
C.带根号的都是无理数; D.无限小数都是无理数.
A
2.对于数 ,下列说法中正确的是( ).
3
-
2
A.它是有理数; B.它是整数;
C.它是分数; D.它是无理数.
D
课堂练习
3.下列实数中:-1.414, , , , , , ,
0.1010010001,其中无理数的个数有 ( ).
22
7
π
2
-
-8
3
25
7
2
3
A.2个; B.3个; C.4个; D.5个.
B
4.下列说法中,正确的是 ( ).
A.实数分为正实数和负实数; B.不带根号的数都是有理数;
C. 无理数包括正无理数和负无理数; D.无理数不是实数.
C
课堂总结
1.什么样的数叫做无理数?试举出几个无理数的例子.
2.什么样的数叫做实数?你会对实数进行分类码?
作业布置
今天作业
课本P15页第1、2 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
