2023年江苏省常州市中天实验学校中考数学一轮复习学案 反比例函数(2)k的几何意义 (1)(无答案)
文档属性
| 名称 | 2023年江苏省常州市中天实验学校中考数学一轮复习学案 反比例函数(2)k的几何意义 (1)(无答案) | 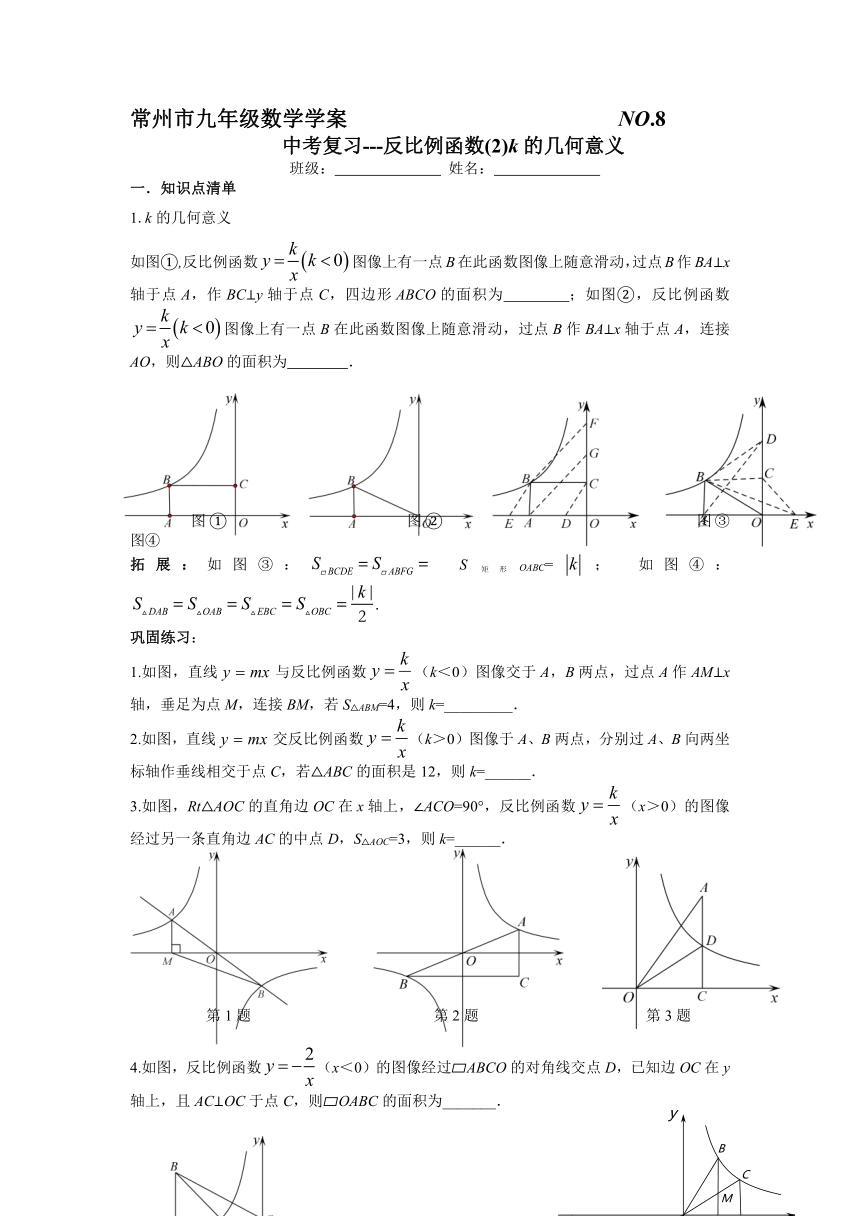 | |
| 格式 | docx | ||
| 文件大小 | 477.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 19:59:20 | ||
图片预览

文档简介
常州市九年级数学学案 NO.8
中考复习---反比例函数(2)k的几何意义
班级: 姓名:
一.知识点清单
1.k的几何意义
如图①,反比例函数图像上有一点B在此函数图像上随意滑动,过点B作BA⊥x轴于点A,作BC⊥y轴于点C,四边形ABCO的面积为 ;如图②,反比例函数图像上有一点B在此函数图像上随意滑动,过点B作BA⊥x轴于点A,连接AO,则△ABO的面积为 .
图① 图② 图③ 图④
拓展:如图③: S矩形OABC=; 如图④:.
巩固练习:
1.如图,直线与反比例函数(k<0)图像交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k=_________.
2.如图,直线交反比例函数(k>0)图像于A、B两点,分别过A、B向两坐标轴作垂线相交于点C,若△ABC的面积是12,则k=______.
3.如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数(x>0)的图像经过另一条直角边AC的中点D,S△AOC=3,则k=______.
第1题 第2题 第3题
4.如图,反比例函数(x<0)的图像经过 ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则 OABC的面积为_______.
第4题 第5题 第6题
5.如图,已知反比例函数(k>0,x>0)的图像经过Rt△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k= .
6.如图所示,在平面直角坐标系xOy中,点A,B,C为反比例函数上不同的三点,连接OA,OB,OC,过点A作ADy轴于点D,过点B,C分别作BE,CF垂直x轴于点E,F,OC与BE相交于点M,记四边形CMEF的面积分别为则( )
A. B. C. D.
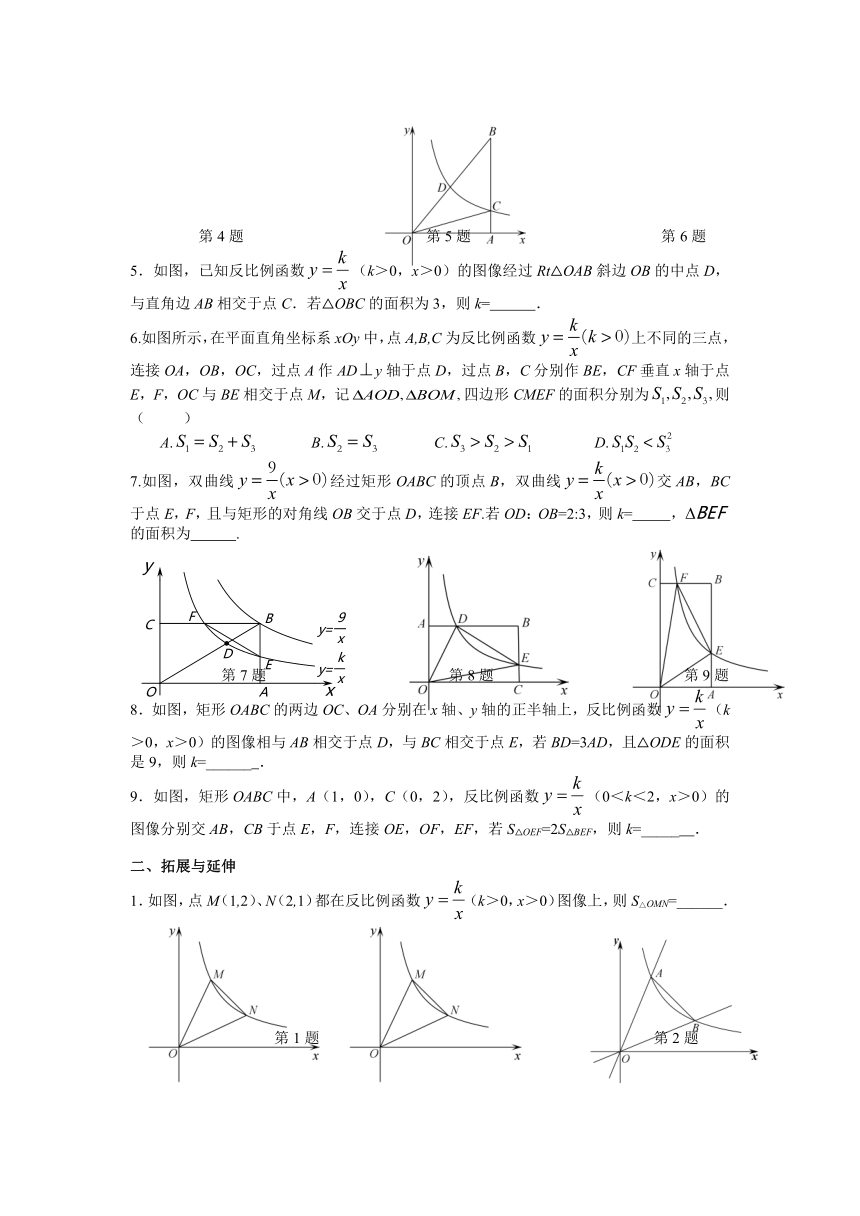
7.如图,双曲线经过矩形OABC的顶点B,双曲线交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.若OD:OB=2:3,则k= ,的面积为 .
第7题 第8题 第9题
8.如图,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(k>0,x>0)的图像相与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=______ .
9.如图,矩形OABC中,A(1,0),C(0,2),反比例函数(0<k<2,x>0)的图像分别交AB,CB于点E,F,连接OE,OF,EF,若S△OEF=2S△BEF,则k=_____ .
二、拓展与延伸
1.如图,点M(1,2)、N(2,1)都在反比例函数(k>0,x>0)图像上,则S△OMN=______.
第1题 第2题
2.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与正比例函数y=kx、y=(k>1)的图象分别交于点A、B.若∠AOB=45°,则△AOB的面积是_______.
3.如图,在平面直角坐标系中,等边和菱形OCDE的边OA,OE都在x轴上,点C在OB边上,,反比例函数的图像经过点B,则k的值为 .
第3题 第4题
4.如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于__________.
编号:8 中考复习——反比例函数(2)当堂训练 姓名:
1.如图,点A是反比例函数(k<0,x<0)的图像上的一点,过A作□ABCD,使点B在x轴上,点D在y轴上,已知□ABCD的面积为6,则k=_________.
第1题 第2题 第3题 第4题
2.如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数(k>0,x>0)的图像上,若△OAB的面积等于6,则k=________.
3.如图,点E、F在反比例函数(x>0)的图像上,直线EF分别与x轴、y轴交于点A、B,
且BE:BF=1:3,则△EOF的面积为 .
4.Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,反比例函数
((k<0,x>0)的图像经过C点及AB的中点D,S△BCD=4,则k=_________.
5.如图,反比例函数(k>0,x>0)的图像与矩形AOBC的边AC交于E,且CE=2AE,与另一边BC交于点D,连接DE,若S△CED=1,则k的值为 .
6.如图,A、B是反比例函数(k>0,x>0)图像上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=OC,S四边形ABDC=9,则k= .
第5题 第6题 第7题
7.如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(﹣1,0),A点的横坐标是2,AB=3BC,反比例函数(m>0)经过A点,双曲线经过C点,则m=_____.
中考复习---反比例函数(2)k的几何意义
班级: 姓名:
一.知识点清单
1.k的几何意义
如图①,反比例函数图像上有一点B在此函数图像上随意滑动,过点B作BA⊥x轴于点A,作BC⊥y轴于点C,四边形ABCO的面积为 ;如图②,反比例函数图像上有一点B在此函数图像上随意滑动,过点B作BA⊥x轴于点A,连接AO,则△ABO的面积为 .
图① 图② 图③ 图④
拓展:如图③: S矩形OABC=; 如图④:.
巩固练习:
1.如图,直线与反比例函数(k<0)图像交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k=_________.
2.如图,直线交反比例函数(k>0)图像于A、B两点,分别过A、B向两坐标轴作垂线相交于点C,若△ABC的面积是12,则k=______.
3.如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数(x>0)的图像经过另一条直角边AC的中点D,S△AOC=3,则k=______.
第1题 第2题 第3题
4.如图,反比例函数(x<0)的图像经过 ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则 OABC的面积为_______.
第4题 第5题 第6题
5.如图,已知反比例函数(k>0,x>0)的图像经过Rt△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k= .
6.如图所示,在平面直角坐标系xOy中,点A,B,C为反比例函数上不同的三点,连接OA,OB,OC,过点A作ADy轴于点D,过点B,C分别作BE,CF垂直x轴于点E,F,OC与BE相交于点M,记四边形CMEF的面积分别为则( )
A. B. C. D.
7.如图,双曲线经过矩形OABC的顶点B,双曲线交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.若OD:OB=2:3,则k= ,的面积为 .
第7题 第8题 第9题
8.如图,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(k>0,x>0)的图像相与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=______ .
9.如图,矩形OABC中,A(1,0),C(0,2),反比例函数(0<k<2,x>0)的图像分别交AB,CB于点E,F,连接OE,OF,EF,若S△OEF=2S△BEF,则k=_____ .
二、拓展与延伸
1.如图,点M(1,2)、N(2,1)都在反比例函数(k>0,x>0)图像上,则S△OMN=______.
第1题 第2题
2.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与正比例函数y=kx、y=(k>1)的图象分别交于点A、B.若∠AOB=45°,则△AOB的面积是_______.
3.如图,在平面直角坐标系中,等边和菱形OCDE的边OA,OE都在x轴上,点C在OB边上,,反比例函数的图像经过点B,则k的值为 .
第3题 第4题
4.如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于__________.
编号:8 中考复习——反比例函数(2)当堂训练 姓名:
1.如图,点A是反比例函数(k<0,x<0)的图像上的一点,过A作□ABCD,使点B在x轴上,点D在y轴上,已知□ABCD的面积为6,则k=_________.
第1题 第2题 第3题 第4题
2.如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数(k>0,x>0)的图像上,若△OAB的面积等于6,则k=________.
3.如图,点E、F在反比例函数(x>0)的图像上,直线EF分别与x轴、y轴交于点A、B,
且BE:BF=1:3,则△EOF的面积为 .
4.Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,反比例函数
((k<0,x>0)的图像经过C点及AB的中点D,S△BCD=4,则k=_________.
5.如图,反比例函数(k>0,x>0)的图像与矩形AOBC的边AC交于E,且CE=2AE,与另一边BC交于点D,连接DE,若S△CED=1,则k的值为 .
6.如图,A、B是反比例函数(k>0,x>0)图像上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=OC,S四边形ABDC=9,则k= .
第5题 第6题 第7题
7.如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(﹣1,0),A点的横坐标是2,AB=3BC,反比例函数(m>0)经过A点,双曲线经过C点,则m=_____.
同课章节目录
