第二十三章 图形的变换 单元练习(无答案) 2022-2023学年京改版九年级数学下册
文档属性
| 名称 | 第二十三章 图形的变换 单元练习(无答案) 2022-2023学年京改版九年级数学下册 |  | |
| 格式 | zip | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 15:53:38 | ||
图片预览

文档简介
第二十三章 图形的变换课后练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、下列四个标志中,是轴对称图形的是( )
A. B. C.D.
2、如图,E是正方形ABCD中CD边上的点,以点A为中心,把△ADE顺时针旋转,得到△ABF.下列角中,是旋转角的是( )
A.∠DAE B.∠EAB C.∠DAB D.∠DAF
3、在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )
A.m=3,n=2 B.m=,n=2 C.m=2,n=3 D.m=,n=
4、已知点M(2,﹣3),点N与点M关于x轴对称,则点N的坐标是( )
A.(﹣2,3) B.(﹣2,﹣3) C.(3,2) D.(2,3)
5、下列所述图形中,不是轴对称图形的是( )
A.矩形 B.平行四边形 C.正五边形 D.正三角形
6、如图,在△ABC中,∠C=90°,AC=3,BC=4,点D、E分别是边AB、BC上的动点,则CD+DE的最小值为( )
A. B. C.4 D.
7、如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到△AB'C',B'C'与BC、AC分别交于点D、点E,设CD+DE=x,△AEC'的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
8、如图,将绕点逆时针旋转55°得到,若,则的度数是( )
A.25° B.30° C.35° D.75°
9、在平面直角坐标系中,点的坐标是,点与点关于轴对称,则点的坐标是( )
A. B. C. D.
10、在平面直角坐标系中,点,关于轴对称点的坐标是( )
A. B. C. D.
二、填空题(共 10 小题)
1、当一个图形在旋转中第一次与自身重合时,我们称此图形转过的角度为旋转对称角,如图,图①、图②、图③按旋转对称角从小到大的顺序排列是_____.(用“<”连接)
2、如图,矩形ABCD绕点A逆时针旋转90°得矩形AEFG,连接CF交AD于点P,M是CF的中点,连接AM交EF于点Q,则下列结论:①AM⊥CF;②CDP≌AEQ;③连接PQ,则PQMQ;④若AE=2,MQ,点P是CM中点,则PD=1.其中,正确结论有_____(填序号).
3、在平面直角坐标系中,以原点为位似中心,作的位似图形,使它与相似比为2,若点的坐标为,则位似图形上与点对应的点的坐标为______.
4、如图,四边形ABCD中,AD∥BC,直线l是它的对称轴,∠B=53°,则∠D的大小为______°.
5、在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点的坐标是,则经过第2021次变换后所得的点的坐标是___________.
6、若点(-1,m)与点(n,2)关于y轴对称,则的值为__________.
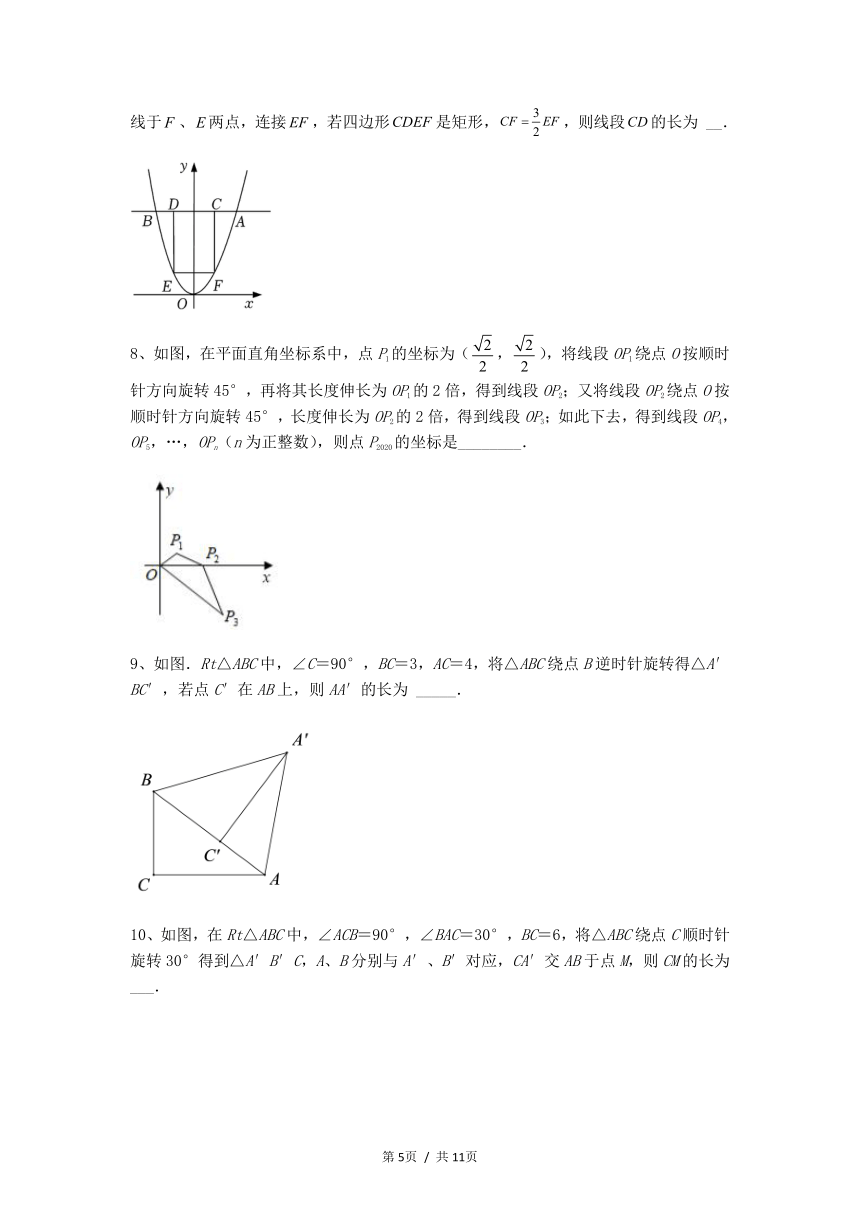
7、如图,在平面直角坐标系中,点在抛物线上,过点作轴的垂线交抛物线于另一点,点、在线段上,分别过点、作轴的垂线交抛物线于、两点,连接,若四边形是矩形,,则线段的长为 __.
8、如图,在平面直角坐标系中,点P1的坐标为(,),将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2;又将线段OP2绕点O按顺时针方向旋转45°,长度伸长为OP2的2倍,得到线段OP3;如此下去,得到线段OP4,OP5,…,OPn(n为正整数),则点P2020的坐标是________.
9、如图.Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC′,若点C′在AB上,则AA′的长为 _____.
10、如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=6,将△ABC绕点C顺时针旋转30°得到△A′B′C,A、B分别与A′、B′对应,CA′交AB于点M,则CM的长为 ___.
三、解答题(共 6 小题)
1、如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.
(1)求证DOB≌AOC;
(2)求∠CEB的大小;
(3)如图2,OAB固定不动,保持△OCD的形状和大小不变,将OCD绕点O旋转(OAB和OCD不能重叠),求∠CEB的大小.
2、如图,在中,,将绕点B按逆时针方向旋转,得到,连接交于点F.
(1)求证:;
(2)求的度数.
3、如图,已知点A(-2,4),B(4,2),C(2,-1).
(1)先画出△ABC,再作出△ABC关于x轴对称的图形△,则点的坐标为________;
(2)P为x轴上一动点,请在图中画出使△PAB的周长最小时的点P,并直接写出此时点P的坐标(保留作图痕迹).
4、在平面直角坐标系xOy中,⊙O的半径为1.
对于线段AB,给出如下定义:若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′,则称线段AB是⊙O的以直线l为对称轴的“反射线段”,直线l称为“反射轴”.
(1)如图,线段CD,EF,GH中是⊙O的以直线l为对称轴的“反射线段”有 ;
(2)已知A点坐标为(0,2),B点坐标为(1,1),
①若线段AB是⊙O的以直线l为对称轴的“反射线段”,求反射轴l与y轴的交点M的坐标.
②若将“反射线段”AB沿直线y=x的方向向上平移一段距离S,其反射轴l与y轴的交点的纵坐标yM的取值范围为yM,求S.
(3)已知点M,N是在以原点为圆心,半径为2的圆上的两个动点,且满足MN=1,若MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,求反射轴l未经过的区域的面积.
(4)已知点M,N是在以(2,0)为圆心,半径为的圆上的两个动点,且满足MN,若MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,请直接写出反射轴l与y轴交点的纵坐标的取值范围.
5、在平面直角坐标系xOy中,对于任意图形G及直线l1,l2,给出如下定义:将图形G先沿直线l1翻折得到图形G1,再将图形G1沿直线l2翻折得到图形G2,则称图形G2是图形G的伴随图形.
例如:点P(2,1)的伴随图形是点P'(-2,-1).
(1)点Q(-3,-2)的伴随图形点Q'的坐标为 ;
(2)已知A(t,1),B(t-3,1),C(t,3),直线m经过点(1,1).
①当t=-1,且直线m与y轴平行时,点A的伴随图形点A'的坐标为 ;
②当直线m经过原点时,若△ABC的伴随图形上只存在两个与x轴的距离为1的点,直接写出t的取值范围.
6、如图在平面坐标系中,的三个顶点的坐标分别是,,.
(1)将向右平移三个单位长度得到,在平面直角坐标系中做出.
(2)以原点O为位似中心,在第一象限内将放大为原来的2倍得到,做出.
第1页 / 共11页
班级:________ 姓名:________
一、单选题(共 10 小题)
1、下列四个标志中,是轴对称图形的是( )
A. B. C.D.
2、如图,E是正方形ABCD中CD边上的点,以点A为中心,把△ADE顺时针旋转,得到△ABF.下列角中,是旋转角的是( )
A.∠DAE B.∠EAB C.∠DAB D.∠DAF
3、在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )
A.m=3,n=2 B.m=,n=2 C.m=2,n=3 D.m=,n=
4、已知点M(2,﹣3),点N与点M关于x轴对称,则点N的坐标是( )
A.(﹣2,3) B.(﹣2,﹣3) C.(3,2) D.(2,3)
5、下列所述图形中,不是轴对称图形的是( )
A.矩形 B.平行四边形 C.正五边形 D.正三角形
6、如图,在△ABC中,∠C=90°,AC=3,BC=4,点D、E分别是边AB、BC上的动点,则CD+DE的最小值为( )
A. B. C.4 D.
7、如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到△AB'C',B'C'与BC、AC分别交于点D、点E,设CD+DE=x,△AEC'的面积为y,则y与x的函数图象大致为( )
A. B.
C. D.
8、如图,将绕点逆时针旋转55°得到,若,则的度数是( )
A.25° B.30° C.35° D.75°
9、在平面直角坐标系中,点的坐标是,点与点关于轴对称,则点的坐标是( )
A. B. C. D.
10、在平面直角坐标系中,点,关于轴对称点的坐标是( )
A. B. C. D.
二、填空题(共 10 小题)
1、当一个图形在旋转中第一次与自身重合时,我们称此图形转过的角度为旋转对称角,如图,图①、图②、图③按旋转对称角从小到大的顺序排列是_____.(用“<”连接)
2、如图,矩形ABCD绕点A逆时针旋转90°得矩形AEFG,连接CF交AD于点P,M是CF的中点,连接AM交EF于点Q,则下列结论:①AM⊥CF;②CDP≌AEQ;③连接PQ,则PQMQ;④若AE=2,MQ,点P是CM中点,则PD=1.其中,正确结论有_____(填序号).
3、在平面直角坐标系中,以原点为位似中心,作的位似图形,使它与相似比为2,若点的坐标为,则位似图形上与点对应的点的坐标为______.
4、如图,四边形ABCD中,AD∥BC,直线l是它的对称轴,∠B=53°,则∠D的大小为______°.
5、在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点的坐标是,则经过第2021次变换后所得的点的坐标是___________.
6、若点(-1,m)与点(n,2)关于y轴对称,则的值为__________.
7、如图,在平面直角坐标系中,点在抛物线上,过点作轴的垂线交抛物线于另一点,点、在线段上,分别过点、作轴的垂线交抛物线于、两点,连接,若四边形是矩形,,则线段的长为 __.
8、如图,在平面直角坐标系中,点P1的坐标为(,),将线段OP1绕点O按顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2;又将线段OP2绕点O按顺时针方向旋转45°,长度伸长为OP2的2倍,得到线段OP3;如此下去,得到线段OP4,OP5,…,OPn(n为正整数),则点P2020的坐标是________.
9、如图.Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC′,若点C′在AB上,则AA′的长为 _____.
10、如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=6,将△ABC绕点C顺时针旋转30°得到△A′B′C,A、B分别与A′、B′对应,CA′交AB于点M,则CM的长为 ___.
三、解答题(共 6 小题)
1、如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.
(1)求证DOB≌AOC;
(2)求∠CEB的大小;
(3)如图2,OAB固定不动,保持△OCD的形状和大小不变,将OCD绕点O旋转(OAB和OCD不能重叠),求∠CEB的大小.
2、如图,在中,,将绕点B按逆时针方向旋转,得到,连接交于点F.
(1)求证:;
(2)求的度数.
3、如图,已知点A(-2,4),B(4,2),C(2,-1).
(1)先画出△ABC,再作出△ABC关于x轴对称的图形△,则点的坐标为________;
(2)P为x轴上一动点,请在图中画出使△PAB的周长最小时的点P,并直接写出此时点P的坐标(保留作图痕迹).
4、在平面直角坐标系xOy中,⊙O的半径为1.
对于线段AB,给出如下定义:若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′,则称线段AB是⊙O的以直线l为对称轴的“反射线段”,直线l称为“反射轴”.
(1)如图,线段CD,EF,GH中是⊙O的以直线l为对称轴的“反射线段”有 ;
(2)已知A点坐标为(0,2),B点坐标为(1,1),
①若线段AB是⊙O的以直线l为对称轴的“反射线段”,求反射轴l与y轴的交点M的坐标.
②若将“反射线段”AB沿直线y=x的方向向上平移一段距离S,其反射轴l与y轴的交点的纵坐标yM的取值范围为yM,求S.
(3)已知点M,N是在以原点为圆心,半径为2的圆上的两个动点,且满足MN=1,若MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,求反射轴l未经过的区域的面积.
(4)已知点M,N是在以(2,0)为圆心,半径为的圆上的两个动点,且满足MN,若MN是⊙O的以直线l为对称轴的“反射线段”,当M点在圆上运动一周时,请直接写出反射轴l与y轴交点的纵坐标的取值范围.
5、在平面直角坐标系xOy中,对于任意图形G及直线l1,l2,给出如下定义:将图形G先沿直线l1翻折得到图形G1,再将图形G1沿直线l2翻折得到图形G2,则称图形G2是图形G的
例如:点P(2,1)的
(1)点Q(-3,-2)的
(2)已知A(t,1),B(t-3,1),C(t,3),直线m经过点(1,1).
①当t=-1,且直线m与y轴平行时,点A的
②当直线m经过原点时,若△ABC的
6、如图在平面坐标系中,的三个顶点的坐标分别是,,.
(1)将向右平移三个单位长度得到,在平面直角坐标系中做出.
(2)以原点O为位似中心,在第一象限内将放大为原来的2倍得到,做出.
第1页 / 共11页
