2022-2023学年人教版七年级数学下册8.1 二元一次方程组 同步测试卷(无答案)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册8.1 二元一次方程组 同步测试卷(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 39.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 14:13:32 | ||
图片预览


文档简介
8.1 二元一次方程组 同步测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 若是二元一次方程的一个解,则的值是( )
A. B. C. D.
2. 某校计划购买篮球和排球共个,其中篮球每个元,排球每个元.若购买篮球和排球共花费元,该校购买篮球和排球各多少个?设购买篮球个,购买排球个,根据题意列出方程组正确的是( )
A. B.
C. D.
3. 二元一次方程有无数个解,下列四组值中不是该方程的解的是 ( )
A. B. C. D.
4. 将变形,用含的代数式表示,正确的是( )
A. B. C. D.
5. 若是关于,的二元一次方程,则的值为( )
A. B. 或 C. D.
6. 若方程组的解是,则方程组的解是( )
A. B. C. D.
7. 某电视台在黄金时段的分钟广告时间内,计划插播长度为秒和秒的两种广告秒的广告每播一次收费万元,秒的广告每播一次收费万元若要求每种广告播放不少于次,则电视台在播放时收益最大的播放方式是( )
A. 秒的广告播放次,秒的广告播放次
B. 秒的广告播放次,秒的广告播放次
C. 秒的广告播放次,秒的广告播放次
D. 秒的广告播放次,秒的广告播放次
8. 一辆轿车行驶小时的路程比一辆卡车行驶小时的路程少千米.如果设轿车平均速度为千米小时,卡车的平均速度为千米小时,则( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
9. 已知是关于,的二元一次方程的解,则 .
10. 在二元一次方程中,若,则 若,则 若,则 .
11. 若关于,的二元一次方程组的解为则多项式可以是 写出一个即可.
12. 笔记本元本,钢笔元支,某同学购买笔记本和钢笔恰好用去元,那么最多购买钢笔______支.
13. 方程组是关于,的二元一次方程组,则的值等于 .
14. 若是关于,的二元一次方程,则的值是
若方程组是关于,的二元一次方程组,则的值是 .
15. 若方程组是关于,的二元一次方程组,则______.
16. 甲、乙、丙三名同学同时解一道题:若方程组的解是求方程组的解三个人根据各自的想法展开讨论.
甲说:“这个题目好像条件不够,不能求解”乙说:“两个方程组的系数有一定的规律,可以试试”丙说:“能不能把第二个方程组的两个方程的两边都除以,通过换元的方法来解决呢”参考他们的讨论,你认为这个题目的解应为 .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知二元一次方程.
用含的代数式表示.
根据给出的值,求出对应的的值,填入表内.
______ ______ ______ ______ ______
写出方程的五个解.
18. 本小题分
根据下表中给出的或的值填空,使每对数都是二元一次方程的解.
______ ______ ______
______ ______ ______
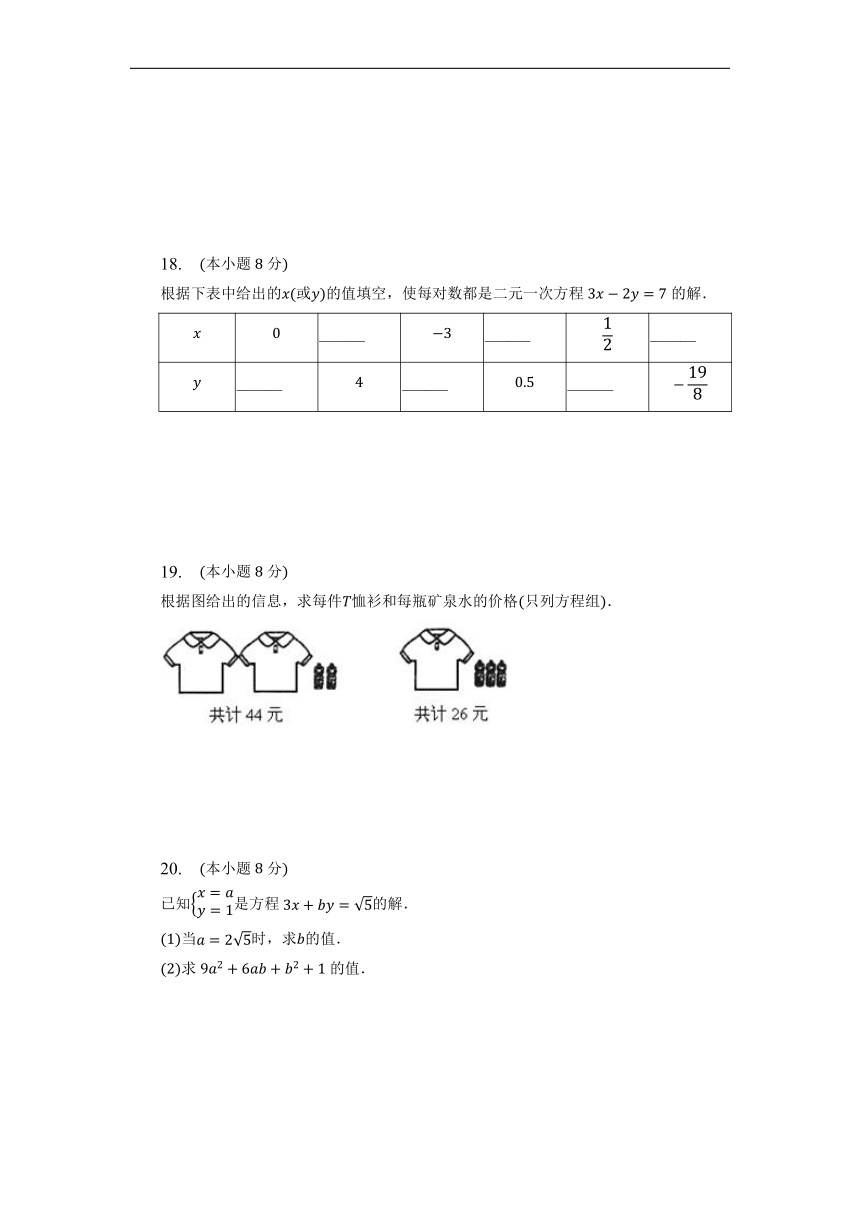
19. 本小题分
根据图给出的信息,求每件恤衫和每瓶矿泉水的价格只列方程组.
20. 本小题分
已知是方程的解.
当时,求的值.
求的值.
21. 本小题分
已知:是的算术平方根,是的算术平方根,求的值.
22. 本小题分
若实数的平方根为方程的一组解.
求的值;
若的小数部分为,求的值.
23. 本小题分
明明发现二元一次方程中,,,他忽然想到:若整系数方程有整数解,则,反之,若,则整系数方程有整数解其中表示,的最大公约数,表示能整除根据这种方法判定下列二元一次方程有无整数解.
.
24. 本小题分
在平面直角坐标系中,你能把二元一次方程的一个解用一个点表示出来吗?标出一些以方程的解为坐标的点过这些点中的任意两点作直线,你有什么发现?在这条直线上任取一点,这个点的坐标是方程的解吗?
以方程的解为坐标的点的全体叫做方程的图象根据上面的探究想一想:方程的图象是什么.
一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线根据这个结论,在同一平面直角坐标系中画出二元一次方程组中的两个二元一次方程的图象.
由这两个二元一次方程的图象,你能得出这个二元一次方程组的解吗?
25. 本小题分
阅读下列材料:
材料一:最大公约数是指两个或多个整数共有的约数中最大的一个.
我们将两个整数,的最大公约数表示为,如:,.
材料二:求的一组整数解,主要分为三个步骤:
第一步,用表示,得
第二步,找一个整数,使得是的倍数,为更容易找到这样的,将变形为,即只需是的倍数即可,因此可取
第三步,将代入,得,是原方程的一组整数解.
材料三:若关于,的二元一次方程均为整数的整数解为则它的所有整数解为为整数.
利用题中材料,解决下列问题:
求方程的一组整数解
求方程的几组正整数解.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 若是二元一次方程的一个解,则的值是( )
A. B. C. D.
2. 某校计划购买篮球和排球共个,其中篮球每个元,排球每个元.若购买篮球和排球共花费元,该校购买篮球和排球各多少个?设购买篮球个,购买排球个,根据题意列出方程组正确的是( )
A. B.
C. D.
3. 二元一次方程有无数个解,下列四组值中不是该方程的解的是 ( )
A. B. C. D.
4. 将变形,用含的代数式表示,正确的是( )
A. B. C. D.
5. 若是关于,的二元一次方程,则的值为( )
A. B. 或 C. D.
6. 若方程组的解是,则方程组的解是( )
A. B. C. D.
7. 某电视台在黄金时段的分钟广告时间内,计划插播长度为秒和秒的两种广告秒的广告每播一次收费万元,秒的广告每播一次收费万元若要求每种广告播放不少于次,则电视台在播放时收益最大的播放方式是( )
A. 秒的广告播放次,秒的广告播放次
B. 秒的广告播放次,秒的广告播放次
C. 秒的广告播放次,秒的广告播放次
D. 秒的广告播放次,秒的广告播放次
8. 一辆轿车行驶小时的路程比一辆卡车行驶小时的路程少千米.如果设轿车平均速度为千米小时,卡车的平均速度为千米小时,则( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
9. 已知是关于,的二元一次方程的解,则 .
10. 在二元一次方程中,若,则 若,则 若,则 .
11. 若关于,的二元一次方程组的解为则多项式可以是 写出一个即可.
12. 笔记本元本,钢笔元支,某同学购买笔记本和钢笔恰好用去元,那么最多购买钢笔______支.
13. 方程组是关于,的二元一次方程组,则的值等于 .
14. 若是关于,的二元一次方程,则的值是
若方程组是关于,的二元一次方程组,则的值是 .
15. 若方程组是关于,的二元一次方程组,则______.
16. 甲、乙、丙三名同学同时解一道题:若方程组的解是求方程组的解三个人根据各自的想法展开讨论.
甲说:“这个题目好像条件不够,不能求解”乙说:“两个方程组的系数有一定的规律,可以试试”丙说:“能不能把第二个方程组的两个方程的两边都除以,通过换元的方法来解决呢”参考他们的讨论,你认为这个题目的解应为 .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
已知二元一次方程.
用含的代数式表示.
根据给出的值,求出对应的的值,填入表内.
______ ______ ______ ______ ______
写出方程的五个解.
18. 本小题分
根据下表中给出的或的值填空,使每对数都是二元一次方程的解.
______ ______ ______
______ ______ ______
19. 本小题分
根据图给出的信息,求每件恤衫和每瓶矿泉水的价格只列方程组.
20. 本小题分
已知是方程的解.
当时,求的值.
求的值.
21. 本小题分
已知:是的算术平方根,是的算术平方根,求的值.
22. 本小题分
若实数的平方根为方程的一组解.
求的值;
若的小数部分为,求的值.
23. 本小题分
明明发现二元一次方程中,,,他忽然想到:若整系数方程有整数解,则,反之,若,则整系数方程有整数解其中表示,的最大公约数,表示能整除根据这种方法判定下列二元一次方程有无整数解.
.
24. 本小题分
在平面直角坐标系中,你能把二元一次方程的一个解用一个点表示出来吗?标出一些以方程的解为坐标的点过这些点中的任意两点作直线,你有什么发现?在这条直线上任取一点,这个点的坐标是方程的解吗?
以方程的解为坐标的点的全体叫做方程的图象根据上面的探究想一想:方程的图象是什么.
一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线根据这个结论,在同一平面直角坐标系中画出二元一次方程组中的两个二元一次方程的图象.
由这两个二元一次方程的图象,你能得出这个二元一次方程组的解吗?
25. 本小题分
阅读下列材料:
材料一:最大公约数是指两个或多个整数共有的约数中最大的一个.
我们将两个整数,的最大公约数表示为,如:,.
材料二:求的一组整数解,主要分为三个步骤:
第一步,用表示,得
第二步,找一个整数,使得是的倍数,为更容易找到这样的,将变形为,即只需是的倍数即可,因此可取
第三步,将代入,得,是原方程的一组整数解.
材料三:若关于,的二元一次方程均为整数的整数解为则它的所有整数解为为整数.
利用题中材料,解决下列问题:
求方程的一组整数解
求方程的几组正整数解.
