17.1.1勾股定理 课件(共22张PPT)【2023春人教版八下数学优质备课】
文档属性
| 名称 | 17.1.1勾股定理 课件(共22张PPT)【2023春人教版八下数学优质备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十七章 勾股定理
17.1勾股定理
第1课时 勾股定理
了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
核心素养目标:
培养在实际生活中发现问题总结规律的意识和能力。
介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习。
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了A、B、C面积之间的数量关系进而发现直角三角形三边的某种数量关系.
数学家毕达哥拉斯的小故事
毕达哥拉斯
A
B
C
情景引入:
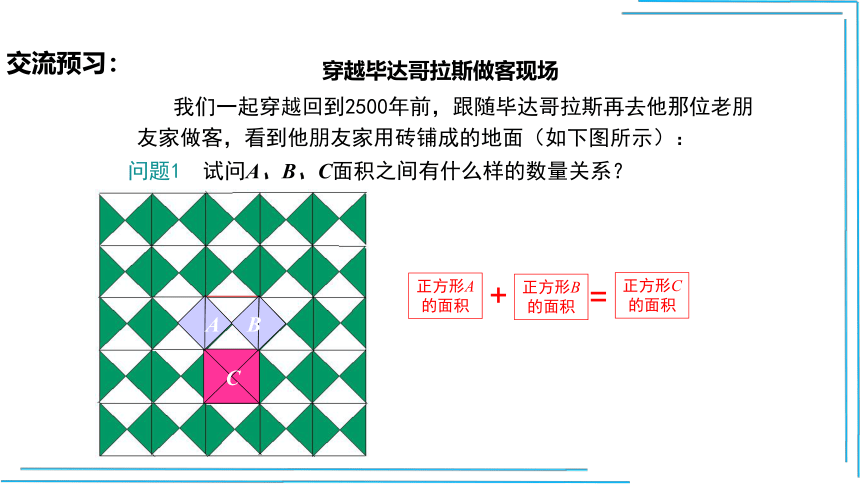
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用砖铺成的地面(如下图所示):
A
B
C
穿越毕达哥拉斯做客现场
问题1 试问A、B、C面积之间有什么样的数量关系?
正方形A的面积
正方形B的面积
正方形C的面积
+
=
交流预习:
A
B
C
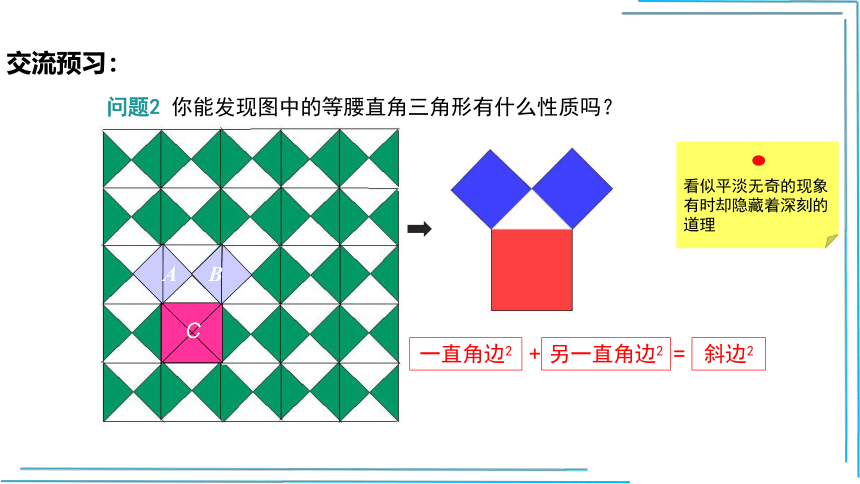
问题2 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
看似平淡无奇的现象有时却隐藏着深刻的道理
交流预习:
图1-2
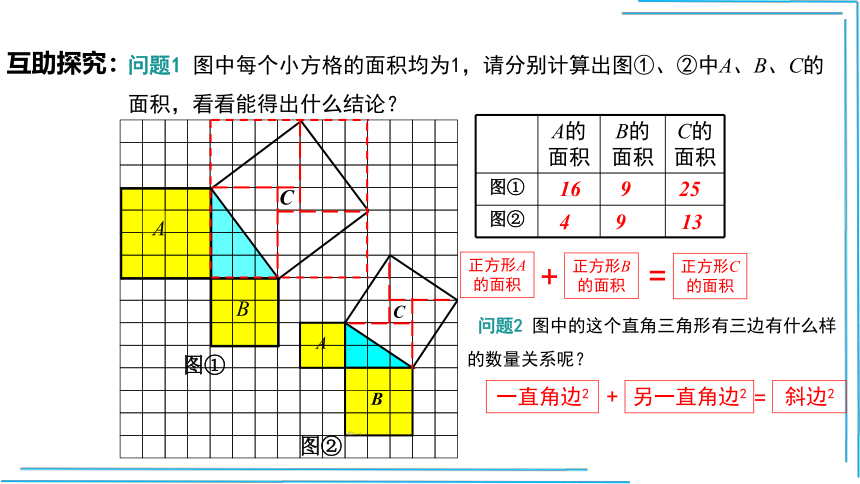
问题1 图中每个小方格的面积均为1,请分别计算出图①、②中A、B、C的面积,看看能得出什么结论?
图①
图②
A
B
A
B
C
C
A的 面积 B的 面积 C的
面积
图①
图②
16
9
25
4
9
13
正方形A的面积
正方形B的面积
正方形C的面积
+
=
问题2 图中的这个直角三角形有三边有什么样的数量关系呢?
一直角边2
另一直角边2
斜边2
+
=
互助探究:
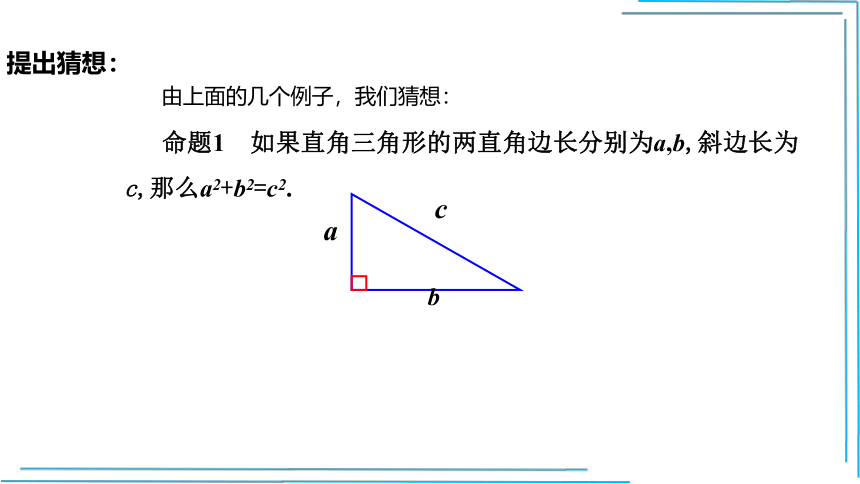
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
由上面的几个例子,我们猜想:
提出猜想:
赵爽
证明命题1的方法有很多,下面介绍我国古人赵爽的证法。
如图,这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形(黄色).
验证猜想:
c
b
a
黄
实
朱实
赵爽弦图
a
b
b
c
a
b
c
c2
b2
a2
=
+
这种用拼图的验证勾股定理的方法叫做弦图法
a
验证猜想:
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
赵爽弦图
证明:
c
b
a
黄
实
朱实
验证猜想:
赵爽所用这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
这样我们就证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称为勾股定理(Pythagoras theorem)
“赵爽弦图”通过对图形的切割、拼接,巧妙地利用面积关系证明了勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
感受数学文化:
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾
股
弦
即:勾2+股2=弦2
勾股定理:
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
c
b
a
例题精讲:
1、设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:由勾股定理得52+122=c2 ,
c=13;
解:由勾股定理得62+b2=102,
b=8;
解:由勾股定理得a2+152=252 ,
a=20.
a
c
b
a
b
c
跟踪练习:教材24页练习
A
B
C
D
2.如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积。
625
跟踪练习:教材24页练习
E
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
证明
课堂小结:
1. 若一个直角三角形的两直角边长分别为9和12,则斜边的长为( )
A.13 B.17 C. 15 D.18
2.若一个直角三角形的斜边长为17,一条直角边长为15,则
另一直角边长为( )
A.8 B.40 C.50 D.36
3.在Rt△ABC中,∠C=90°,若a︰b=3︰4,c=100,则a= _____,b = ______.
C
A
60
80
课堂检测:
课后作业:
必做题:整理课堂中所提到的勾股定理的证明方法;
选做题:通过上网等查找有关勾股定理的有关史料、趣事及其他证明方法
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十七章 勾股定理
17.1勾股定理
第1课时 勾股定理
了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
核心素养目标:
培养在实际生活中发现问题总结规律的意识和能力。
介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习。
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了A、B、C面积之间的数量关系进而发现直角三角形三边的某种数量关系.
数学家毕达哥拉斯的小故事
毕达哥拉斯
A
B
C
情景引入:
我们一起穿越回到2500年前,跟随毕达哥拉斯再去他那位老朋友家做客,看到他朋友家用砖铺成的地面(如下图所示):
A
B
C
穿越毕达哥拉斯做客现场
问题1 试问A、B、C面积之间有什么样的数量关系?
正方形A的面积
正方形B的面积
正方形C的面积
+
=
交流预习:
A
B
C
问题2 你能发现图中的等腰直角三角形有什么性质吗?
一直角边2
另一直角边2
斜边2
+
=
看似平淡无奇的现象有时却隐藏着深刻的道理
交流预习:
图1-2
问题1 图中每个小方格的面积均为1,请分别计算出图①、②中A、B、C的面积,看看能得出什么结论?
图①
图②
A
B
A
B
C
C
A的 面积 B的 面积 C的
面积
图①
图②
16
9
25
4
9
13
正方形A的面积
正方形B的面积
正方形C的面积
+
=
问题2 图中的这个直角三角形有三边有什么样的数量关系呢?
一直角边2
另一直角边2
斜边2
+
=
互助探究:
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
a
b
c
由上面的几个例子,我们猜想:
提出猜想:
赵爽
证明命题1的方法有很多,下面介绍我国古人赵爽的证法。
如图,这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形(黄色).
验证猜想:
c
b
a
黄
实
朱实
赵爽弦图
a
b
b
c
a
b
c
c2
b2
a2
=
+
这种用拼图的验证勾股定理的方法叫做弦图法
a
验证猜想:
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
赵爽弦图
证明:
c
b
a
黄
实
朱实
验证猜想:
赵爽所用这种方法是我国古代常用的“出入相补法”.在西方,人们称勾股定理为毕达哥拉斯定理.
这样我们就证实了命题1的正确性,命题1与直角三角形的边有关,我国把它称为勾股定理(Pythagoras theorem)
“赵爽弦图”通过对图形的切割、拼接,巧妙地利用面积关系证明了勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
感受数学文化:
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
a、b、c为正数
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
公式变形:
勾
股
弦
即:勾2+股2=弦2
勾股定理:
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
c
b
a
例题精讲:
1、设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:由勾股定理得52+122=c2 ,
c=13;
解:由勾股定理得62+b2=102,
b=8;
解:由勾股定理得a2+152=252 ,
a=20.
a
c
b
a
b
c
跟踪练习:教材24页练习
A
B
C
D
2.如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积。
625
跟踪练习:教材24页练习
E
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
证明
课堂小结:
1. 若一个直角三角形的两直角边长分别为9和12,则斜边的长为( )
A.13 B.17 C. 15 D.18
2.若一个直角三角形的斜边长为17,一条直角边长为15,则
另一直角边长为( )
A.8 B.40 C.50 D.36
3.在Rt△ABC中,∠C=90°,若a︰b=3︰4,c=100,则a= _____,b = ______.
C
A
60
80
课堂检测:
课后作业:
必做题:整理课堂中所提到的勾股定理的证明方法;
选做题:通过上网等查找有关勾股定理的有关史料、趣事及其他证明方法
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
