12.2 三角形全等的判定(第1课时)课件
文档属性
| 名称 | 12.2 三角形全等的判定(第1课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 544.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-07 21:25:55 | ||
图片预览






文档简介
课件18张PPT。八年级 上册12.2 三角形全等的判定 (第1课时)课件说明 本课是在学生已经学习了全等三角形的概念和性质
的基础上,探究三角形全等的条件,并以 “边边
边”条件为例,理解、掌握三角形全等的判定.学习目标:
1.构建三角形全等条件的探索思路,体会研究几何
问题的方法.
2.探索并理解“边边边”判定方法,会用“边边
边”判定方法证明三角形全等.
3.会用尺规作一个角等于已知角,了解作图的道理.
学习重点:
构建三角形全等条件的探索思路,“边边边”判定
方法.
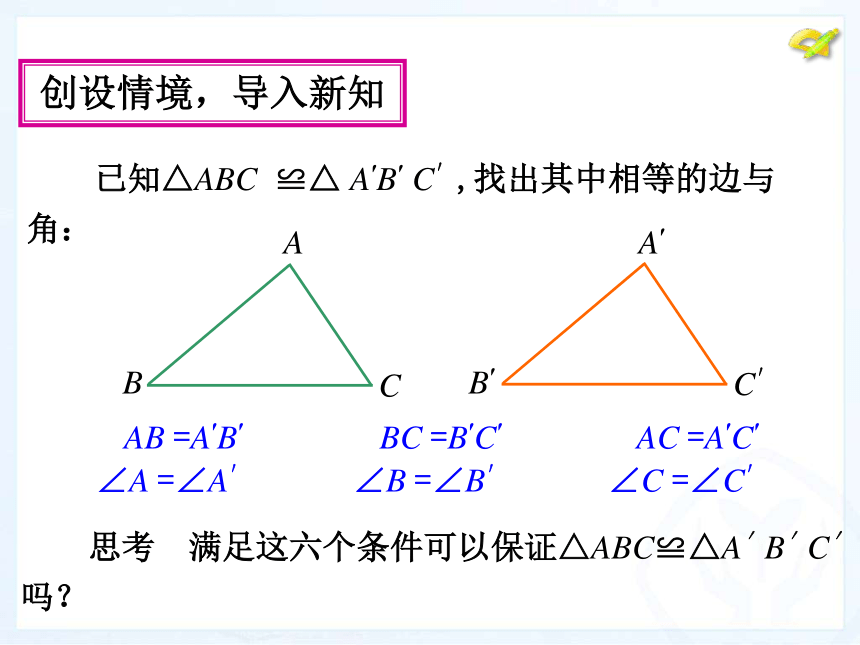
课件说明∠A =∠A′AB =A′B′ 已知△ABC ≌△ A′B′ C′,找出其中相等的边与
角: 思考 满足这六个条件可以保证△ABC≌△A′B′C′
吗?创设情境,导入新知∠B =∠B′BC =B′C′∠C =∠C′AC =A′C′ 追问1 当满足一个条件时, △ABC 与△A′B′C′
全等吗?动脑思考,分类辨析 思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗? 思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗?两个条件 追问2 当满足两个条件时, △ABC 与△A′B′C′
全等吗?动脑思考,分类辨析 思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗?三个条件 追问3 当满足三个条件时, △ABC 与△A′B′C′
全等吗?满足三个条件时,又分为几种情况呢?动脑思考,分类辨析 画法:
(1)画线段B′C′=BC ;
(2)分别以B′、C′为圆心,BA、BC 为半径画弧,两
弧交于点A′;
(3)连接线段A′B′,A′C′.动手操作,验证猜想 先任意画出一个△ABC,再画出一个△A′B′C′,
使A′B′= AB,B′C′= BC,A′C′= AC.把画好的
△A′B′C′剪下,放到△ABC 上,它们全等吗? 边边边公理:
三边对应相等的两个三角形全等.简写为“边边
边”或“SSS”.动脑思考,得出结论 思考 作图的结果反映了什么规律?你能用文字语
言和符号语言概括吗?在△ABC 与 △ A′B′C′中,∴ △ABC ≌△A′B′C′ (SSS). 判断两个三角形全等的推理
过程,叫做证明三角形全等. 用符号语言表达:动脑思考,得出结论证明:∵ D 是BC 中点,
∴ BD =DC.
在△ABD 与△ACD 中,∴ △ABD ≌ △ACD ( SSS ).应用所学,例题解析 例 如图,有一个三角形钢架,AB =AC ,AD 是
连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD . 作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D; 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析ODBCA 作法:
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′; 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析O′C′A′ODBCA 作法:
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′; 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析O′D′C′A′ODBCA 作法:
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析O′D′B′C′A′ODBCA 作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析(1)本节课学习了哪些主要内容?
(2)探索三角形全等的条件,其基本思路是什么?
(3)“SSS”判定方法有何作用?课堂小结布置作业 必做题:教科书习题12.2第1、9 题;
选做题:如图,△ABC 和△EFD 中,AB =EF,
AC =ED,点B,D,C,F 在一条直线上.
(1)添加一个条件,由“SSS”可判定△ABC≌△EFD;
(2)在(1)的基础上,
求证:AB∥EF.
的基础上,探究三角形全等的条件,并以 “边边
边”条件为例,理解、掌握三角形全等的判定.学习目标:
1.构建三角形全等条件的探索思路,体会研究几何
问题的方法.
2.探索并理解“边边边”判定方法,会用“边边
边”判定方法证明三角形全等.
3.会用尺规作一个角等于已知角,了解作图的道理.
学习重点:
构建三角形全等条件的探索思路,“边边边”判定
方法.
课件说明∠A =∠A′AB =A′B′ 已知△ABC ≌△ A′B′ C′,找出其中相等的边与
角: 思考 满足这六个条件可以保证△ABC≌△A′B′C′
吗?创设情境,导入新知∠B =∠B′BC =B′C′∠C =∠C′AC =A′C′ 追问1 当满足一个条件时, △ABC 与△A′B′C′
全等吗?动脑思考,分类辨析 思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗? 思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗?两个条件 追问2 当满足两个条件时, △ABC 与△A′B′C′
全等吗?动脑思考,分类辨析 思考 如果只满足这些条件中的一部分,那么能保
证△ABC ≌△A′B′C′吗?三个条件 追问3 当满足三个条件时, △ABC 与△A′B′C′
全等吗?满足三个条件时,又分为几种情况呢?动脑思考,分类辨析 画法:
(1)画线段B′C′=BC ;
(2)分别以B′、C′为圆心,BA、BC 为半径画弧,两
弧交于点A′;
(3)连接线段A′B′,A′C′.动手操作,验证猜想 先任意画出一个△ABC,再画出一个△A′B′C′,
使A′B′= AB,B′C′= BC,A′C′= AC.把画好的
△A′B′C′剪下,放到△ABC 上,它们全等吗? 边边边公理:
三边对应相等的两个三角形全等.简写为“边边
边”或“SSS”.动脑思考,得出结论 思考 作图的结果反映了什么规律?你能用文字语
言和符号语言概括吗?在△ABC 与 △ A′B′C′中,∴ △ABC ≌△A′B′C′ (SSS). 判断两个三角形全等的推理
过程,叫做证明三角形全等. 用符号语言表达:动脑思考,得出结论证明:∵ D 是BC 中点,
∴ BD =DC.
在△ABD 与△ACD 中,∴ △ABD ≌ △ACD ( SSS ).应用所学,例题解析 例 如图,有一个三角形钢架,AB =AC ,AD 是
连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD . 作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D; 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析ODBCA 作法:
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′; 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析O′C′A′ODBCA 作法:
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′; 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析O′D′C′A′ODBCA 作法:
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析O′D′B′C′A′ODBCA 作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB. 已知:∠AOB.求作: ∠A′O′B′=∠AOB. 用尺规作一个角等于已知角.应用所学,例题解析(1)本节课学习了哪些主要内容?
(2)探索三角形全等的条件,其基本思路是什么?
(3)“SSS”判定方法有何作用?课堂小结布置作业 必做题:教科书习题12.2第1、9 题;
选做题:如图,△ABC 和△EFD 中,AB =EF,
AC =ED,点B,D,C,F 在一条直线上.
(1)添加一个条件,由“SSS”可判定△ABC≌△EFD;
(2)在(1)的基础上,
求证:AB∥EF.
