6.4 生活中的圆周运动 (二) 课件 高一下学期物理人教版(2019)必修第二册(共15张PPT)
文档属性
| 名称 | 6.4 生活中的圆周运动 (二) 课件 高一下学期物理人教版(2019)必修第二册(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 373.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-02 10:46:26 | ||
图片预览






文档简介
(共15张PPT)
6.4 生活中的圆周运动(二)
竖直面内的圆周运动
在生活中的圆周运动中,有一类属于竖直面内的圆周运动,例如过山车、水流星,由于重力也作用在竖直平面内,所以这种圆周运动有着特殊的规律……
如图水流星,演员用一根轻绳连着两个装满水的容器,在竖直平面旋转时,哪怕到了最高点,容器口向下,水也不会流下。
1.轻绳和轻杆模型概述
在竖直平面内做圆周运动的物体,运动至轨道最高点时的受力情况可分为两类:一是无支撑(如球与绳连接,沿内轨道的“过山车”等),称为轻绳模型;二是有支撑(如球与杆连接,小球在弯管内运动等),称为轻杆模型。
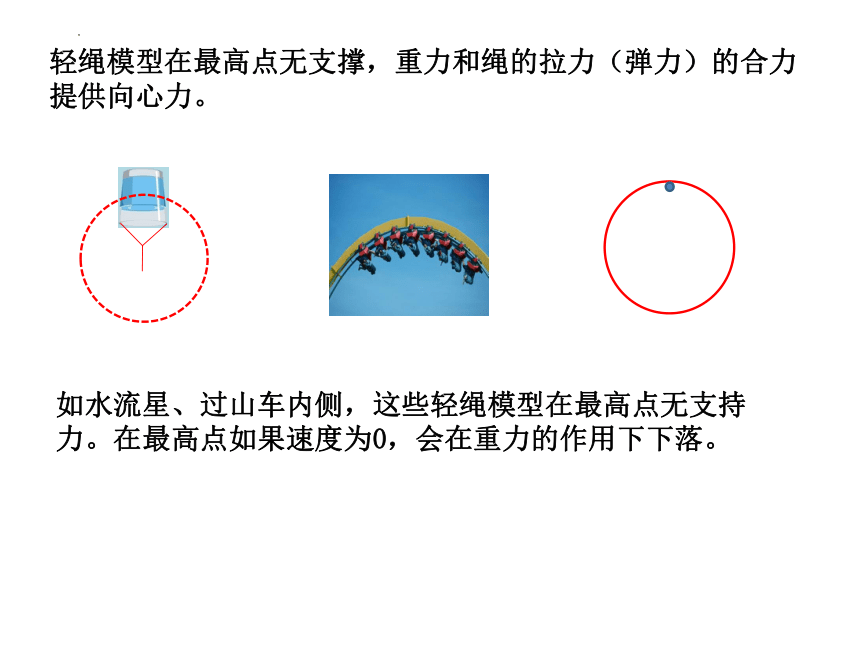
轻绳模型在最高点无支撑,重力和绳的拉力(弹力)的合力提供向心力。
如水流星、过山车内侧,这些轻绳模型在最高点无支持力。在最高点如果速度为0,会在重力的作用下下落。
轻绳模型在最高点,质点受重力mg、绳的拉力(容器底或轨道的弹力)F,这两个力方向都向下,mg + F =Fn
F=0时,向心力最小,为Fn=mg,
由mg= ,则v= 。
所以轻绳模型能够过最高点的临界条件是v≥ 。
轻杆在最高点可支撑也可提供拉力,最高点重力和杆(管道)弹力的合力提供向心力。
如管道、过山车外侧,这些轻杆模型在最高点有支持力。在最高点如果速度为0,不会下落。
轻杆模型在最高点,质点受重力mg、弹力(不同情况下方向可能不同)F,向心力的表达形式也可能不同。
轻杆模型能够过最高点的临界条件是v≥ 。
[例 1] 如图所示,长度 L=0.4 m 的轻绳系一小球,小球在竖直平面内做圆周运动,小球的质量 m=0.5 kg,小球半径不计,g 取 10 m/s 2 ,求:
(1)小球刚好通过最高点时的速度大小;
(2)小球通过最高点时的速度大小为 4 m/s 时,绳的拉力大小;
(3)若轻绳能承受的最大张力为 45 N,小球整个运动过程中速度大小的最大值。
[拓展训练 1].如图所示,过山车的轨道可视为竖直平面内半径为 R 的圆轨道。质量为m 的游客随过山车一起运动,当游客以速度 v 经过圆轨道的最高点时( )
A.处于超重状态
B.向心加速度方向竖直向下
C.速度 v 的大小一定为
D.座位对游客的作用力为
在解答竖直平面内物体的圆周运动问题时,首先要确定是属于轻绳模型,还是轻杆模型,然后注意区分两者在最高点的最小速度的要求,区分绳与杆的施力特点,必要时还要根据牛顿运动定律列式求解。
[例 2] 长 L=0.5 m 的轻杆一端连接着一个零件 A,A 的质量 m=2 kg。现让 A 在竖直平面内绕 O 点做匀速圆周运动,如图所示,在 A 通过最高点时,求下列两种情况下A 对轻杆的作用力:(取 g=10 m/s 2 )
(1)A 的速率为 1 m/s;
(2)A 的速率为 4 m/s。
[拓展训练 2].如图所示,一长为 L 的轻质细杆一端与质量为 m 的小球(可视为质点)相连,另一端可绕 O 点转动,现使轻杆在同一竖直面内匀速转动,测得小球的向心加速度大小为g(g 为当地的重力加速度),下列说法正确的是( )
A.小球的线速度大小为 gL
B.小球运动到最高点时处于完全失重状态
C.当轻杆转到水平位置时,轻杆对小球作用力的方向指向圆心 O
D.轻杆在匀速转动过程中,轻杆对小球作用力的最大值为 mg
[拓展训练 3].如图所示,轻杆一端固定一质量为 m 的小球,以另一端 O 为圆心,使小球在竖直面内做半径为 R 的圆周运动,以下说法正确的是( )
A.小球过最高点时,杆对球的弹力不可能等于零
B.小球过最高点时,速度至少为
C.小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定不小于杆对球的作用力
D.小球过最高点时,杆对球的作用力一定与小球所受重力方向相反
再见
6.4 生活中的圆周运动(二)
竖直面内的圆周运动
在生活中的圆周运动中,有一类属于竖直面内的圆周运动,例如过山车、水流星,由于重力也作用在竖直平面内,所以这种圆周运动有着特殊的规律……
如图水流星,演员用一根轻绳连着两个装满水的容器,在竖直平面旋转时,哪怕到了最高点,容器口向下,水也不会流下。
1.轻绳和轻杆模型概述
在竖直平面内做圆周运动的物体,运动至轨道最高点时的受力情况可分为两类:一是无支撑(如球与绳连接,沿内轨道的“过山车”等),称为轻绳模型;二是有支撑(如球与杆连接,小球在弯管内运动等),称为轻杆模型。
轻绳模型在最高点无支撑,重力和绳的拉力(弹力)的合力提供向心力。
如水流星、过山车内侧,这些轻绳模型在最高点无支持力。在最高点如果速度为0,会在重力的作用下下落。
轻绳模型在最高点,质点受重力mg、绳的拉力(容器底或轨道的弹力)F,这两个力方向都向下,mg + F =Fn
F=0时,向心力最小,为Fn=mg,
由mg= ,则v= 。
所以轻绳模型能够过最高点的临界条件是v≥ 。
轻杆在最高点可支撑也可提供拉力,最高点重力和杆(管道)弹力的合力提供向心力。
如管道、过山车外侧,这些轻杆模型在最高点有支持力。在最高点如果速度为0,不会下落。
轻杆模型在最高点,质点受重力mg、弹力(不同情况下方向可能不同)F,向心力的表达形式也可能不同。
轻杆模型能够过最高点的临界条件是v≥ 。
[例 1] 如图所示,长度 L=0.4 m 的轻绳系一小球,小球在竖直平面内做圆周运动,小球的质量 m=0.5 kg,小球半径不计,g 取 10 m/s 2 ,求:
(1)小球刚好通过最高点时的速度大小;
(2)小球通过最高点时的速度大小为 4 m/s 时,绳的拉力大小;
(3)若轻绳能承受的最大张力为 45 N,小球整个运动过程中速度大小的最大值。
[拓展训练 1].如图所示,过山车的轨道可视为竖直平面内半径为 R 的圆轨道。质量为m 的游客随过山车一起运动,当游客以速度 v 经过圆轨道的最高点时( )
A.处于超重状态
B.向心加速度方向竖直向下
C.速度 v 的大小一定为
D.座位对游客的作用力为
在解答竖直平面内物体的圆周运动问题时,首先要确定是属于轻绳模型,还是轻杆模型,然后注意区分两者在最高点的最小速度的要求,区分绳与杆的施力特点,必要时还要根据牛顿运动定律列式求解。
[例 2] 长 L=0.5 m 的轻杆一端连接着一个零件 A,A 的质量 m=2 kg。现让 A 在竖直平面内绕 O 点做匀速圆周运动,如图所示,在 A 通过最高点时,求下列两种情况下A 对轻杆的作用力:(取 g=10 m/s 2 )
(1)A 的速率为 1 m/s;
(2)A 的速率为 4 m/s。
[拓展训练 2].如图所示,一长为 L 的轻质细杆一端与质量为 m 的小球(可视为质点)相连,另一端可绕 O 点转动,现使轻杆在同一竖直面内匀速转动,测得小球的向心加速度大小为g(g 为当地的重力加速度),下列说法正确的是( )
A.小球的线速度大小为 gL
B.小球运动到最高点时处于完全失重状态
C.当轻杆转到水平位置时,轻杆对小球作用力的方向指向圆心 O
D.轻杆在匀速转动过程中,轻杆对小球作用力的最大值为 mg
[拓展训练 3].如图所示,轻杆一端固定一质量为 m 的小球,以另一端 O 为圆心,使小球在竖直面内做半径为 R 的圆周运动,以下说法正确的是( )
A.小球过最高点时,杆对球的弹力不可能等于零
B.小球过最高点时,速度至少为
C.小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定不小于杆对球的作用力
D.小球过最高点时,杆对球的作用力一定与小球所受重力方向相反
再见
