8.2.3解一元一次不等式(2)--一元一次不等式的应用 课件(共27张PPT)
文档属性
| 名称 | 8.2.3解一元一次不等式(2)--一元一次不等式的应用 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 980.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 17:43:01 | ||
图片预览








文档简介
(共27张PPT)
8.2.3解一元一次不等式(2)
华师大版 七年级 下册
教学目标
教学目标:1.会通过列一元一次不等式去解决生活中的实际问题,经历
“实际问题抽象为不等式模型”的过程.
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论
思想在用不等式解决实际问题中的应用.
教学重点:在实际问题中,运用一元一次不等式解决实际问题.
教学难点:在实际问题中,运用一元一次不等式解决实际问题.
新知导入
情境引入
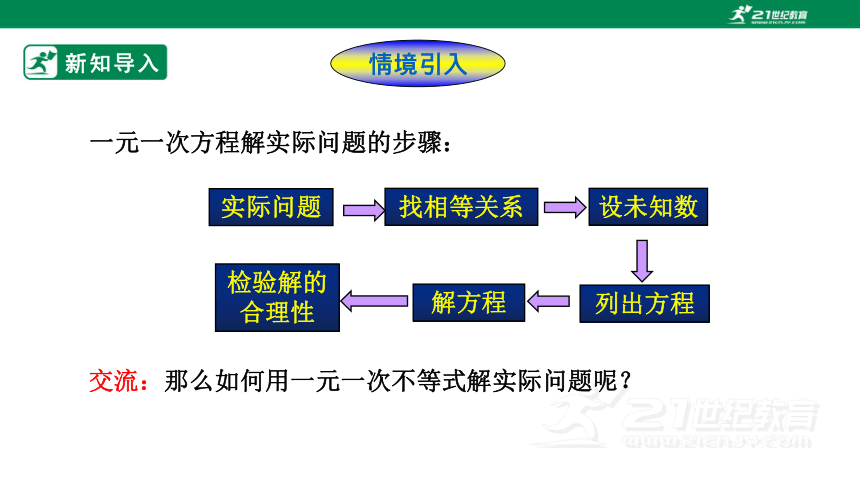
一元一次方程解实际问题的步骤:
实际问题
设未知数
找相等关系
列出方程
检验解的合理性
解方程
交流:那么如何用一元一次不等式解实际问题呢?
新知讲解
合作学习
在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者能通过预选赛.育才中学有25名学生通过了预选赛,通过者至少应答对多少道题?有哪些可能情形?
问题
(1)试解决这个问题(不限定方法),你是用什么方法解决的?
(2)如果利用不等式的知识解决这个问题,在得到不等式的解集以后,如何给出原问题的答案?应该如何表述?
讨论
(1)方法一:方程解答
解:设答对x道题,得分是80分.
由题意得
10x-5(20-x)=80,
解得:x=12.
答:通过者至少应答对12道题.
(2)方法二:不等式解答
解:设通过者至少应答对x道题,
由题意得
10x-5(20-x)≥80,
解得:x ≥ 12.
答:通过者至少应答对12道题.
若将题意改成“答错1题扣5分,不答题不得分”即在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错1题扣5分,不答题不得分,总得分不少于80分者通过预选赛。育才中学25名学生通过了预选赛,他们分别可能答对了多少道题?
变式题
解:因为不少于80分者通过.
设他们可能答对x道,其它题不答,则:10x+0×(20-x)>80 x>8
则答对题可能为:9,810,11,12,13,14,15,16,17,18,19,20 因为共20题,20-8=12,也就是不答的题小于12,即不答的题小于12道.
设他们可能答对x道,其它题答错,则:10x-5×(20-x)>80
x>12
则答对题可能为:13,14,15,16,17,18,19,20 因为共20题,20-12=8 也就是答错的题小于8,即答错的题小于8道
则:他们可能答对的题大于8道
他们可能答错的题小于8道
他们可能不答的题小于12道
提炼概念
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
典例精讲
例1:学校图书馆搬迁,有15万册图书,原准备每天在一个班级的劳动课上,安排一个小组同学帮助搬运图书,两天共搬了1.8万册。如果要求在7天内搬完,设每个小组搬运图书数相同,则在以后几天内,每天至少安排几个小组搬书?
解 设:每天至少安排x个小组,由题意得
答:每天至少安排3个小组.
例2:某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则 40x-90×40-40x·10%≥900.
解得
x ≥ 125.
答:每套童装的售价至少是125元.
归纳概念
解一元一次不等式应用题的步骤
(1)审题,寻找不等关系;
(2)直接或间接设未知数;
(3)列出不等式;
(4)求出不等式的解集;
(5)找出符合实际的值;
(6)作答
课堂练习
1.某种商品的进价为80元,标价为100元,后由于该商品积压,商店准备打折销售,要保证利润率不低于12.5%,该种商品最多可打( )
A. 九折 B. 八折 C. 七折 D. 六折
A
2.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过120分,他至少要答对多少道题?如果设小明答对x道题,则他答错或不答的题数为20-x.根据题意得( )
A. 10x-5(20-x)≥120 B. 10x-5(20-x)≤120
C. 10x-5(20-x)>120 D. 10x-5(20-x)<120
C
3.当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
解: 设小明应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
例3:小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
4.甲、乙两超市以同样价格出售同样的商品,并且给出了不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按90%收费;在乙超市累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家超市购物花费少?
分析:甲乙两超市的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠, 购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若 50+0.95(x-50)>100+0.9(x-100) 即x>150
在甲超市购物花费少;
②若 50+0.95(x-50)<100+0.9(x-100) 即x<150
在乙超市购物花费少;
③若 50+0.95(x-50)=100+0.9(x-100) 即x=150
在甲、乙两超市购物花费一样.
5.疫情期间为了满足口罩需求,某学校决定购进A、B两种型号的口罩.若购进A型口罩2盒,B型口罩1盒,共需200元;若购进A型口罩4盒,B型口罩3盒,共需550元.
(1)求A、B两种型号的口罩每盒各需多少元?
(2)若该学校决定购进这两种型号的口罩共计200盒,考虑到实际需求,要求购进A型号口罩的盒数不超过B型口罩盒数的6倍.那么最多可以购买多少盒A型口罩?
课堂总结
应用一元一次不等式解实际问题的一般步骤:
实际问题
(包含不等关系)
数学问题
(一元一次不等式)
数学问题的解
(不等式的解集)
实际问题的解答
设未知数,列不等式
检验
解不等式
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
8.2.3解一元一次不等式(2)
华师大版 七年级 下册
教学目标
教学目标:1.会通过列一元一次不等式去解决生活中的实际问题,经历
“实际问题抽象为不等式模型”的过程.
2.体会解不等式过程中的化归思想与类比思想,体会分类讨论
思想在用不等式解决实际问题中的应用.
教学重点:在实际问题中,运用一元一次不等式解决实际问题.
教学难点:在实际问题中,运用一元一次不等式解决实际问题.
新知导入
情境引入
一元一次方程解实际问题的步骤:
实际问题
设未知数
找相等关系
列出方程
检验解的合理性
解方程
交流:那么如何用一元一次不等式解实际问题呢?
新知讲解
合作学习
在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者能通过预选赛.育才中学有25名学生通过了预选赛,通过者至少应答对多少道题?有哪些可能情形?
问题
(1)试解决这个问题(不限定方法),你是用什么方法解决的?
(2)如果利用不等式的知识解决这个问题,在得到不等式的解集以后,如何给出原问题的答案?应该如何表述?
讨论
(1)方法一:方程解答
解:设答对x道题,得分是80分.
由题意得
10x-5(20-x)=80,
解得:x=12.
答:通过者至少应答对12道题.
(2)方法二:不等式解答
解:设通过者至少应答对x道题,
由题意得
10x-5(20-x)≥80,
解得:x ≥ 12.
答:通过者至少应答对12道题.
若将题意改成“答错1题扣5分,不答题不得分”即在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错1题扣5分,不答题不得分,总得分不少于80分者通过预选赛。育才中学25名学生通过了预选赛,他们分别可能答对了多少道题?
变式题
解:因为不少于80分者通过.
设他们可能答对x道,其它题不答,则:10x+0×(20-x)>80 x>8
则答对题可能为:9,810,11,12,13,14,15,16,17,18,19,20 因为共20题,20-8=12,也就是不答的题小于12,即不答的题小于12道.
设他们可能答对x道,其它题答错,则:10x-5×(20-x)>80
x>12
则答对题可能为:13,14,15,16,17,18,19,20 因为共20题,20-12=8 也就是答错的题小于8,即答错的题小于8道
则:他们可能答对的题大于8道
他们可能答错的题小于8道
他们可能不答的题小于12道
提炼概念
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
典例精讲
例1:学校图书馆搬迁,有15万册图书,原准备每天在一个班级的劳动课上,安排一个小组同学帮助搬运图书,两天共搬了1.8万册。如果要求在7天内搬完,设每个小组搬运图书数相同,则在以后几天内,每天至少安排几个小组搬书?
解 设:每天至少安排x个小组,由题意得
答:每天至少安排3个小组.
例2:某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则 40x-90×40-40x·10%≥900.
解得
x ≥ 125.
答:每套童装的售价至少是125元.
归纳概念
解一元一次不等式应用题的步骤
(1)审题,寻找不等关系;
(2)直接或间接设未知数;
(3)列出不等式;
(4)求出不等式的解集;
(5)找出符合实际的值;
(6)作答
课堂练习
1.某种商品的进价为80元,标价为100元,后由于该商品积压,商店准备打折销售,要保证利润率不低于12.5%,该种商品最多可打( )
A. 九折 B. 八折 C. 七折 D. 六折
A
2.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过120分,他至少要答对多少道题?如果设小明答对x道题,则他答错或不答的题数为20-x.根据题意得( )
A. 10x-5(20-x)≥120 B. 10x-5(20-x)≤120
C. 10x-5(20-x)>120 D. 10x-5(20-x)<120
C
3.当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
解: 设小明应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
例3:小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
4.甲、乙两超市以同样价格出售同样的商品,并且给出了不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按90%收费;在乙超市累计购物超过50元后,超出50元的部分按95%收费,顾客到哪家超市购物花费少?
分析:甲乙两超市的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠, 购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若 50+0.95(x-50)>100+0.9(x-100) 即x>150
在甲超市购物花费少;
②若 50+0.95(x-50)<100+0.9(x-100) 即x<150
在乙超市购物花费少;
③若 50+0.95(x-50)=100+0.9(x-100) 即x=150
在甲、乙两超市购物花费一样.
5.疫情期间为了满足口罩需求,某学校决定购进A、B两种型号的口罩.若购进A型口罩2盒,B型口罩1盒,共需200元;若购进A型口罩4盒,B型口罩3盒,共需550元.
(1)求A、B两种型号的口罩每盒各需多少元?
(2)若该学校决定购进这两种型号的口罩共计200盒,考虑到实际需求,要求购进A型号口罩的盒数不超过B型口罩盒数的6倍.那么最多可以购买多少盒A型口罩?
课堂总结
应用一元一次不等式解实际问题的一般步骤:
实际问题
(包含不等关系)
数学问题
(一元一次不等式)
数学问题的解
(不等式的解集)
实际问题的解答
设未知数,列不等式
检验
解不等式
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
