10.1全等三角形 课件(共21张PPT) 2022—2023学年鲁教版(五四制)数学七年级下册
文档属性
| 名称 | 10.1全等三角形 课件(共21张PPT) 2022—2023学年鲁教版(五四制)数学七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 16:43:50 | ||
图片预览


文档简介
(共21张PPT)
《数学》( 北师大.七年级 下册 )
七年级数学组
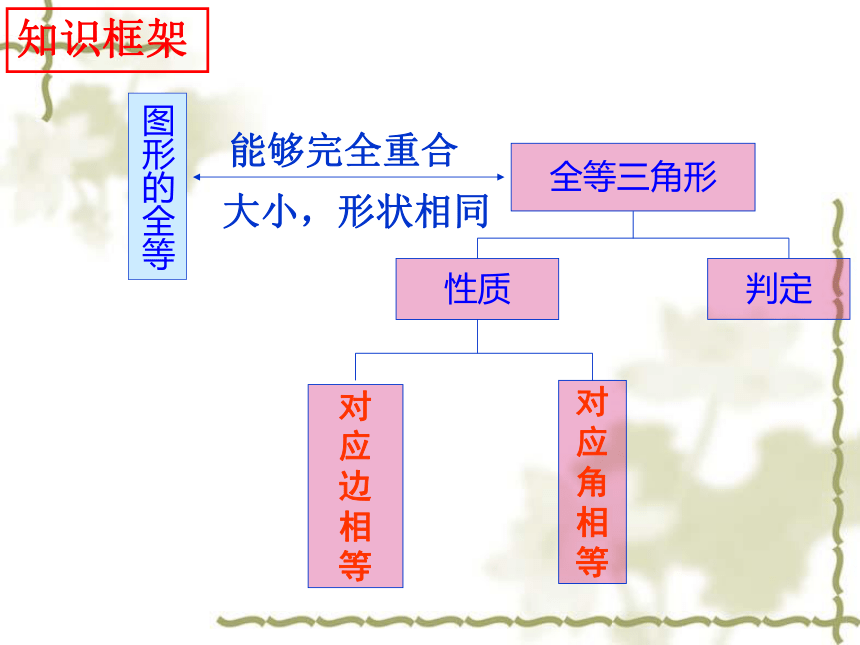
全等三角形
性质
判定
对
应
边
相
等
对
应
角
相
等
能够完全重合
大小,形状相同
知识框架
图形的全等
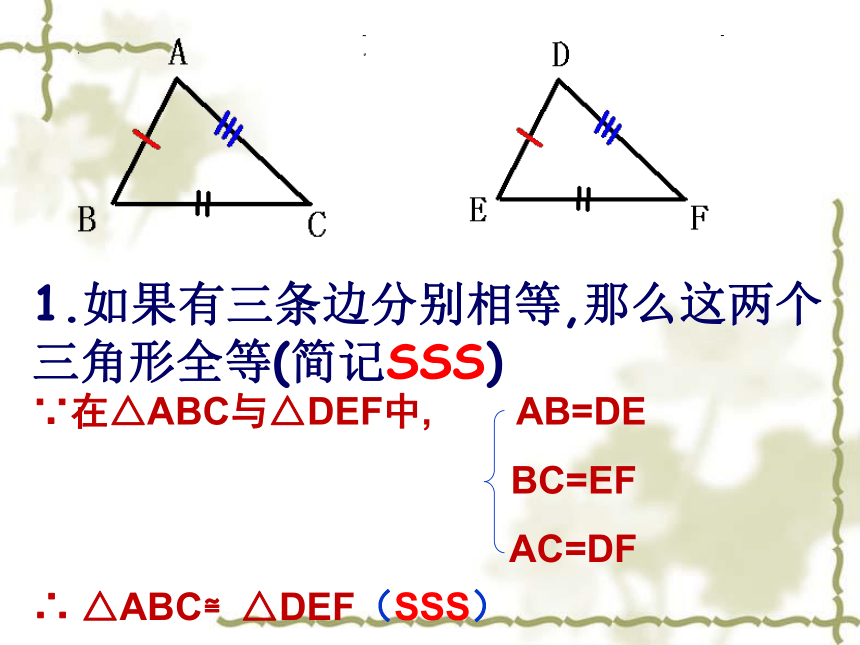
1.如果有三条边分别相等,那么这两个三角形全等(简记SSS)
∵在△ABC与△DEF中, AB=DE
BC=EF
AC=DF
∴ △ABC≌△DEF(SSS)
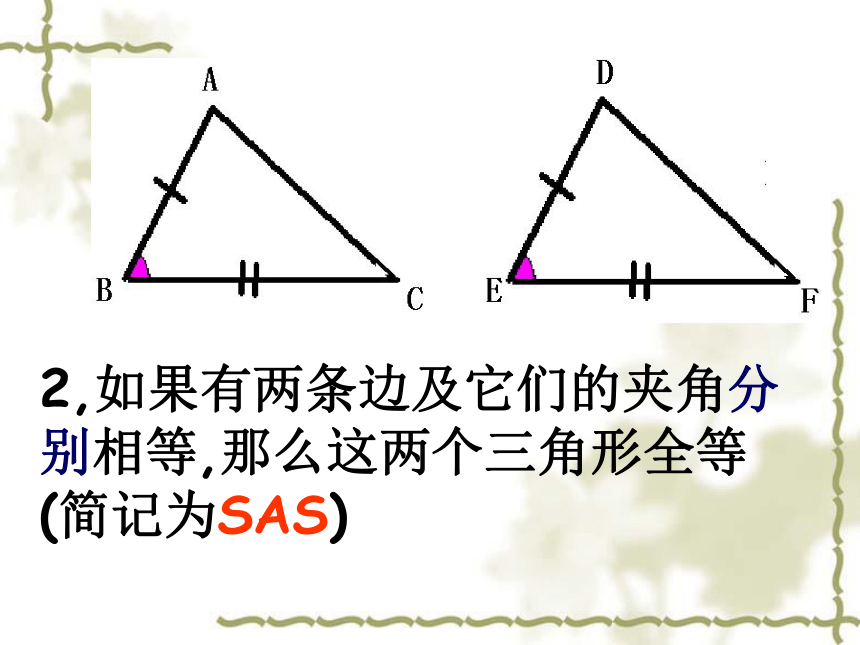
2,如果有两条边及它们的夹角分别相等,那么这两个三角形全等(简记为SAS)
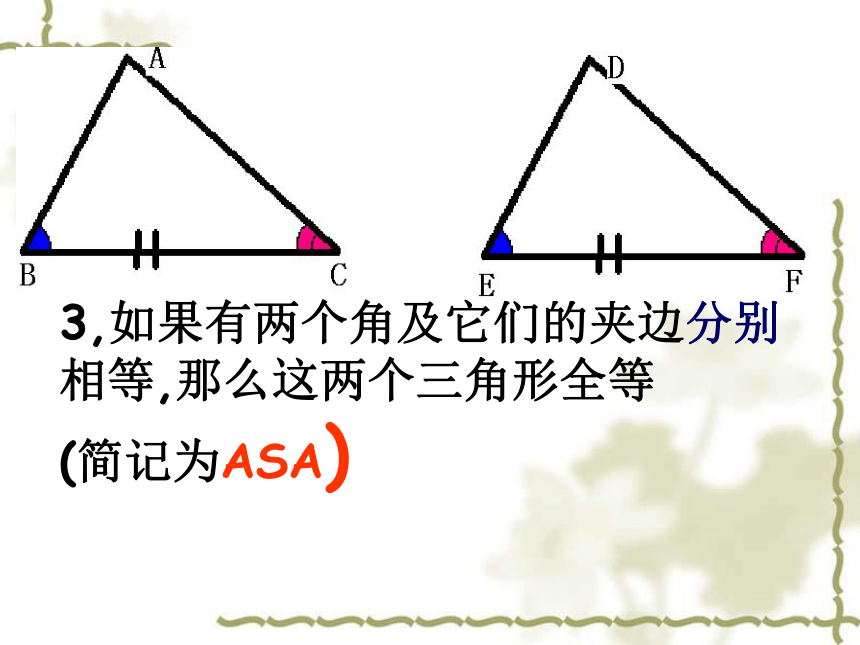
3,如果有两个角及它们的夹边分别相等,那么这两个三角形全等 (简记为ASA)
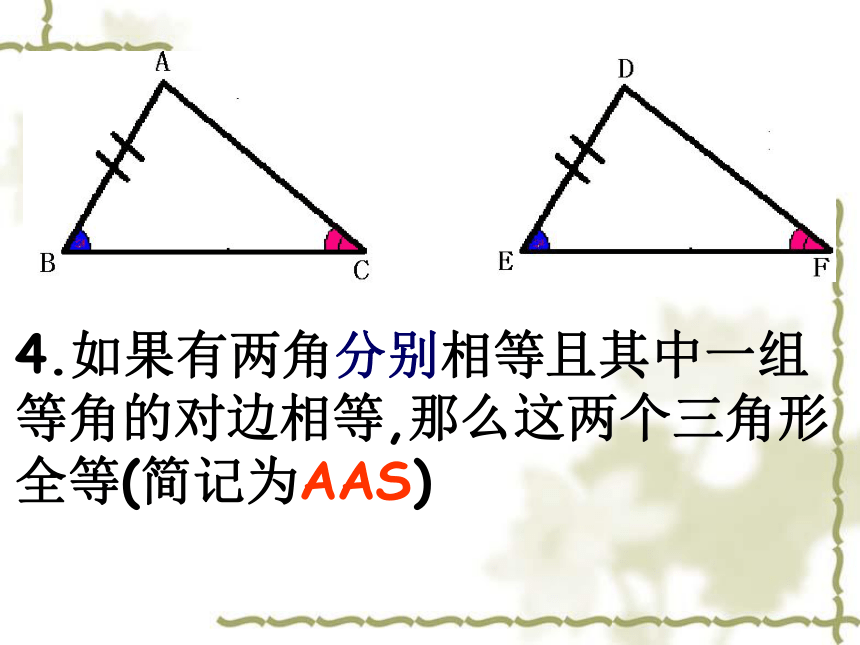
4.如果有两角分别相等且其中一组等角的对边相等,那么这两个三角形全等(简记为AAS)
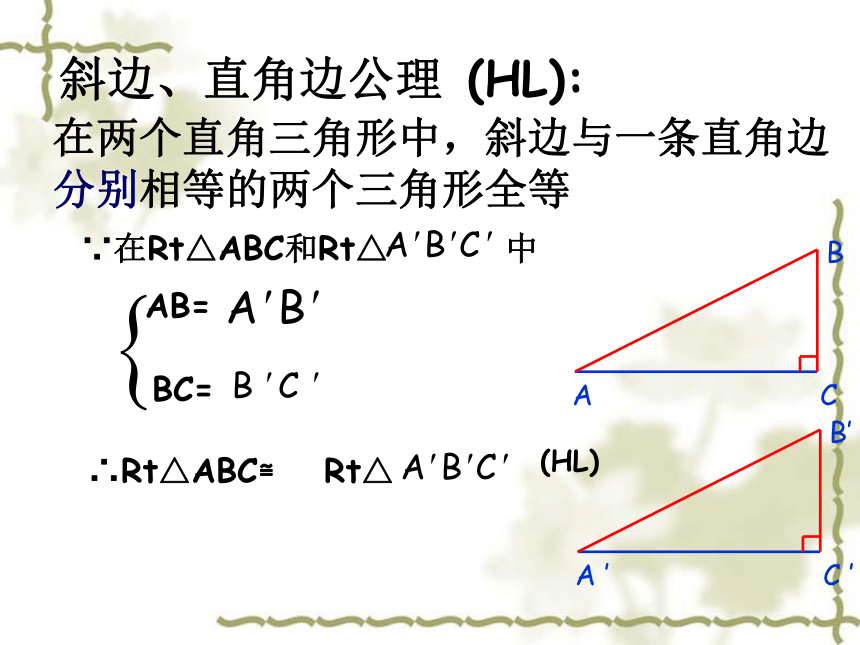
斜边、直角边公理 (HL):
A
B
C
A ′
B′
C ′
∵在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
在两个直角三角形中,斜边与一条直角边分别相等的两个三角形全等
Rt△
(HL)
知识驿站:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
至少一边
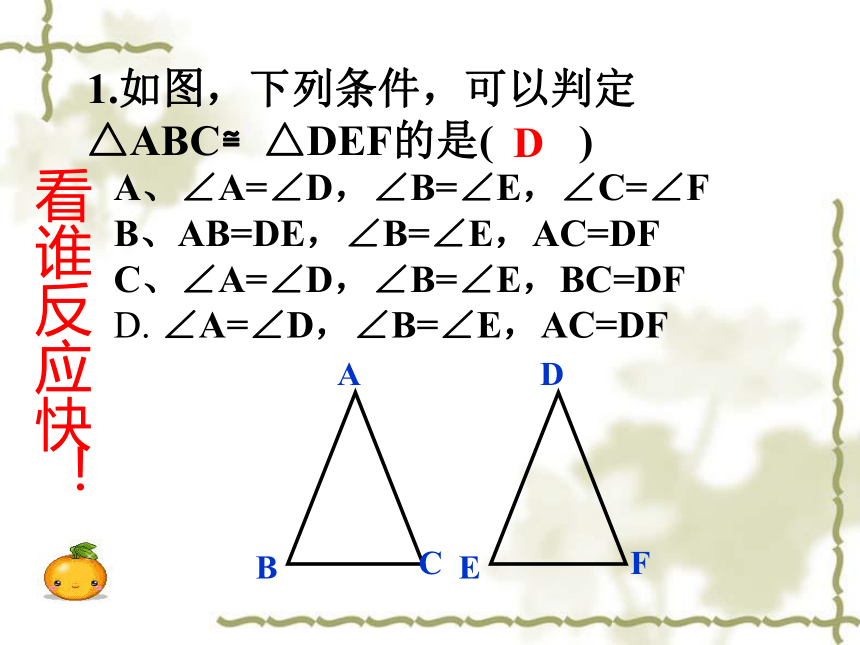
1.如图,下列条件,可以判定△ABC≌△DEF的是( )
D
A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,BC=DF
D. ∠A=∠D,∠B=∠E,AC=DF
A
B
C
D
E
F
看谁反应快!
2.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .
A
B
C
D
1
2
1. 如图,已知AD=AC,要使△ADB≌△ACB,需要添加的一个条件是__________.
添夹角
添第三边
添直角
已知两组边:
∠DAB=∠CAB (SAS)
BD=BC (SSS)
∠D=∠C=90°(HL)
开放问题
B
C
D
A
2、如图,已知△ABC和△DCB中,AB=DC,请补充一个条件_______,使△ABC≌ △DCB。
注意其中的公共边
添夹角
添第三边
添直角
已知两边:
∠ ABC=∠DCB (SAS)
AC=DB (SSS)
∠ A=∠D=90°(HL)
A
B
C
D
3、如图,已知∠C= ∠D,要识别△ABC≌ △ABD,需要添加的一个条件是____________。
添任一角
已知一边一角
(边与角相对)
(AAS)
∠CAB=∠DAB
或者
∠CBA=∠DBA
A
C
B
D
4. 已知∠B=∠E,要识别△ABC≌△AED,需要添加的一个条件是 。
已知两组角:
添夹边
添一角的对边
A
B
C
D
E
AB=AE
AC=AD
或 BC=ED
(ASA)
(AAS)
5. 已知AB=AE,要使△ABC≌△AED,需要添加的一个条件是__________。
已知一组边一组角(边与角相邻):
添夹这个角的另一边
添夹这条边的另一角
添边的对角
AC=AD
∠B=∠E
∠ACB=∠ADE
(SAS)
(ASA)
(AAS)
A
B
C
D
E
6. 已知BC=ED,要使△ABC≌△AED,需要添加的一个条件是__________。
添任一角
已知一组边一组角(边与角相对)
(AAS)
∠B=∠E
或者
∠ACB=∠ADE
(AAS)
A
B
C
D
E
添加AC=AD或者AB=AE可以吗?
8. 已知∠1= ∠2,要识别△ABC≌△CDA,需要添加的一个条件是__________
思路3:
已知一边一角(边与角相邻):
A
B
C
D
2
1
添夹这个角的另一边
添夹这条边的另一角
添边的对角
AD=CB
∠ACD=∠CAB
∠D=∠B
(SAS)
(ASA)
(AAS)
例:用直尺和圆规作一个角等于已知角的示意图如图所示,则说明 的 依据是 。
尺规作图——全等的应用
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA、OB于C、D,再分别以点C、D 为圆心,以大于 长为半径画弧,两弧交于点P,作射线AP,由作法得 的根据是( )
A.SAS B.ASA
C.AAS D.SSS
尺规作图——全等的应用
如图A、B、C在一直线上,△ABD,△BCE都是等边三角形,AE交BD于F,DC交BE于G,求证: ①AE=CD ② BF=BG。
证明:∵△ABD,△BCE是等边三角形。 ∴∠DBA=△EBC=60°
∵ A、B、C共线∴∠DBE=60° ∴∠ABE=∠DBC 在△ABE与△DBC中
AB=DB ∠ABE=∠DBC BE=BC
∴△ABE≌△DBC(SAS) ∴AE=CD
② ∵ △ABE≌△DBC
∴ ∠2=∠1
在△BEF与△BCG中
∠EBF=∠CBG BE=BC ∠2=∠1
∴△BEF≌△BCG(ASA) ∴BF=BG(全等三角形对应边相等)
祝同学们学习进步
再见
《数学》( 北师大.七年级 下册 )
七年级数学组
全等三角形
性质
判定
对
应
边
相
等
对
应
角
相
等
能够完全重合
大小,形状相同
知识框架
图形的全等
1.如果有三条边分别相等,那么这两个三角形全等(简记SSS)
∵在△ABC与△DEF中, AB=DE
BC=EF
AC=DF
∴ △ABC≌△DEF(SSS)
2,如果有两条边及它们的夹角分别相等,那么这两个三角形全等(简记为SAS)
3,如果有两个角及它们的夹边分别相等,那么这两个三角形全等 (简记为ASA)
4.如果有两角分别相等且其中一组等角的对边相等,那么这两个三角形全等(简记为AAS)
斜边、直角边公理 (HL):
A
B
C
A ′
B′
C ′
∵在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
在两个直角三角形中,斜边与一条直角边分别相等的两个三角形全等
Rt△
(HL)
知识驿站:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
至少一边
1.如图,下列条件,可以判定△ABC≌△DEF的是( )
D
A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,BC=DF
D. ∠A=∠D,∠B=∠E,AC=DF
A
B
C
D
E
F
看谁反应快!
2.如图,AB⊥BC,AD⊥DC,
AB=AD.
求证∠1=∠2 .
A
B
C
D
1
2
1. 如图,已知AD=AC,要使△ADB≌△ACB,需要添加的一个条件是__________.
添夹角
添第三边
添直角
已知两组边:
∠DAB=∠CAB (SAS)
BD=BC (SSS)
∠D=∠C=90°(HL)
开放问题
B
C
D
A
2、如图,已知△ABC和△DCB中,AB=DC,请补充一个条件_______,使△ABC≌ △DCB。
注意其中的公共边
添夹角
添第三边
添直角
已知两边:
∠ ABC=∠DCB (SAS)
AC=DB (SSS)
∠ A=∠D=90°(HL)
A
B
C
D
3、如图,已知∠C= ∠D,要识别△ABC≌ △ABD,需要添加的一个条件是____________。
添任一角
已知一边一角
(边与角相对)
(AAS)
∠CAB=∠DAB
或者
∠CBA=∠DBA
A
C
B
D
4. 已知∠B=∠E,要识别△ABC≌△AED,需要添加的一个条件是 。
已知两组角:
添夹边
添一角的对边
A
B
C
D
E
AB=AE
AC=AD
或 BC=ED
(ASA)
(AAS)
5. 已知AB=AE,要使△ABC≌△AED,需要添加的一个条件是__________。
已知一组边一组角(边与角相邻):
添夹这个角的另一边
添夹这条边的另一角
添边的对角
AC=AD
∠B=∠E
∠ACB=∠ADE
(SAS)
(ASA)
(AAS)
A
B
C
D
E
6. 已知BC=ED,要使△ABC≌△AED,需要添加的一个条件是__________。
添任一角
已知一组边一组角(边与角相对)
(AAS)
∠B=∠E
或者
∠ACB=∠ADE
(AAS)
A
B
C
D
E
添加AC=AD或者AB=AE可以吗?
8. 已知∠1= ∠2,要识别△ABC≌△CDA,需要添加的一个条件是__________
思路3:
已知一边一角(边与角相邻):
A
B
C
D
2
1
添夹这个角的另一边
添夹这条边的另一角
添边的对角
AD=CB
∠ACD=∠CAB
∠D=∠B
(SAS)
(ASA)
(AAS)
例:用直尺和圆规作一个角等于已知角的示意图如图所示,则说明 的 依据是 。
尺规作图——全等的应用
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA、OB于C、D,再分别以点C、D 为圆心,以大于 长为半径画弧,两弧交于点P,作射线AP,由作法得 的根据是( )
A.SAS B.ASA
C.AAS D.SSS
尺规作图——全等的应用
如图A、B、C在一直线上,△ABD,△BCE都是等边三角形,AE交BD于F,DC交BE于G,求证: ①AE=CD ② BF=BG。
证明:∵△ABD,△BCE是等边三角形。 ∴∠DBA=△EBC=60°
∵ A、B、C共线∴∠DBE=60° ∴∠ABE=∠DBC 在△ABE与△DBC中
AB=DB ∠ABE=∠DBC BE=BC
∴△ABE≌△DBC(SAS) ∴AE=CD
② ∵ △ABE≌△DBC
∴ ∠2=∠1
在△BEF与△BCG中
∠EBF=∠CBG BE=BC ∠2=∠1
∴△BEF≌△BCG(ASA) ∴BF=BG(全等三角形对应边相等)
祝同学们学习进步
再见
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
