【核心素养目标】24.3.1圆周角定理 教学设计
文档属性
| 名称 | 【核心素养目标】24.3.1圆周角定理 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版九年级下册数学 24.3.1圆周角定理 教学设计
课题 24.3.1圆周角定理 单元 第24单元 学科 数学 年级 九
教材分析 本节在学习了圆心角的基础上,继续学习了圆周角的概念,以及同弧所对的圆周角等于它所对圆心角的一半,并学习了两个推论:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等;半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径。
核心素养分析 本节要求掌握圆周角的概念,理解和运用圆周角定理 ,推导出2个推论:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径”,利用圆周角定理求角和线段等元素,培养了学生推理和计算的能力,同时锻炼了学生几何直观的素养。
学习目标 1.理解圆周角的概念,理解和运用圆周角定理解几何问题2.掌握半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径
重点 理解圆周角的概念,理解和运用圆周角定理解几何问题
难点 掌握半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 经过三点A,B ,C,可以确定一个圆吗 不在同一直线上的三个点确定一个圆.三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC 回顾上节的内容,以培养学生温顾知识,大胆发言的良好习惯。 回顾上节知识,导入本节新课,圆的重要一个内容,圆周角定理。
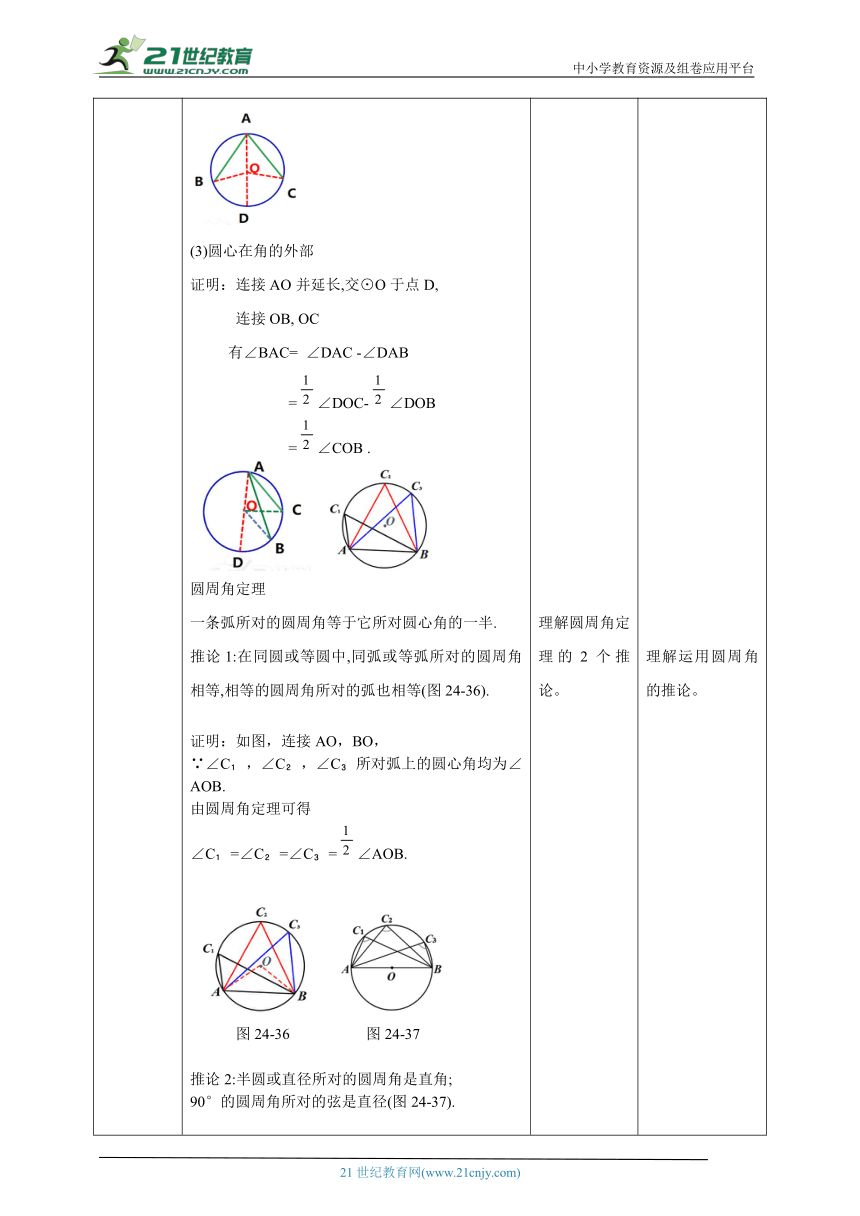
讲授新课 如图24-33,△ABC内接于⊙O,这时∠A的顶点在圆上,∠A的两边AB, AC分别与圆还有另一个公共点。顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角。两个条件必须同时具备,缺一不可圆O中圆周角有哪几个?∠A、∠B和∠C下列图中哪个是圆周角?图(2)是圆周角探究如图24-34 ,若△ABC是等边三角形,⊙O是其外接圆,∠BAC 与∠BOC有什么关系呢?证明:∵△ABC是等边三角形∴∠BAC =∠ABC =∠BCA = 60°,又∵∠BOC =∠AOC =∠AOB =120°,∴∠BAC = ∠BOC任意画一个⊙O及其内接△ABC,用量角器量,∠BAC及∠BOC有什么样关系 一个圆周角的大小与它所对弧上的圆心角有关;前者是后者的二分之一。 以⊙O上任一点A为顶点的圆周角有无数多个,按圆心与圆周角的位置关系,存在下面三种情况,如图24-35.圆心在角的一边上 圆心在角的内部 圆心在角的外部(1)圆心在角的一边上证明:连接OC,∵△OAC是等腰三角形,∴∠A=∠OCA.∴∠BOC=∠A+∠OCA =2∠A即∠A=∠BOC.(2)圆心在角的内部证明:连接AO并延长,交⊙O于点D, 连接OB, OC,∵∠BAC =∠DAC+∠DAB∴∠BAC= ∠DOC+ ∠DOB = ∠BOC.(3)圆心在角的外部证明:连接AO并延长,交⊙O于点D, 连接OB, OC 有∠BAC= ∠DAC -∠DAB =∠DOC-∠DOB =∠COB .圆周角定理一条弧所对的圆周角等于它所对圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等(图24-36).证明:如图,连接AO,BO,∵∠C ,∠C ,∠C 所对弧上的圆心角均为∠AOB.由圆周角定理可得∠C =∠C =∠C =∠AOB.图24-36 图24-37推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径(图24-37).证明:∵A、O、B在一条直线上,∴∠AOB=180°由圆周角定理得 ∠C =∠C =∠C =180°÷2 = 90°.即直径所对的圆周角是直角,同理,90°的圆周角所对的弦AB是直径。例1 如图24-38,AB为⊙O的直径,弦CD交AB于点P,∠ACD =60°,∠ADC =70° ,求∠APC的度数.分析:∠APC等于圆周角∠BAD与∠ADC之和.解:连接BC,则∠ACB =90°,∠DCB = ∠ACB -∠ACD = 90°-60° =30°又∠BAD =∠DCB = 30°,∠APC = ∠BAD +∠ADC =30° +70°=100°. 熟悉圆周角定义,学生独立思考、小组合作讨论,发表自己的见解,大胆建议,学会倾听别的同学的意见。学生思考 从3个角度熟悉证明圆周角与圆心角的关系。理解圆周角定理的2个推论。 理解概念,帮助学生判定圆周角。巩固圆周角的概念 掌握定理的推导和证明过程。理解运用圆周角的推论。
课堂练习 1、如图,△ABC的顶点A,B在⊙O上,点C在⊙O外(O,C在AB同侧),∠AOB=98°,则∠C的度数可能是( )A. 48° B. 49° C. 50° D. 51°解:设AC与⊙O相交于点D,连接BD,∵∠AOB=98°,∴∠ADB= ∠AOB=49°,∵∠ADB是△BCD的一个外角,∴∠C<∠ADB,∴∠C的度数可能是:48°,故选:A.如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )A. 3α+β=180° B. 2α+β=180°C. 3α-β=90° D. 2α-β=90°解:∵OA⊥BC,∴∠AOB=∠AOC=90°,∴∠DBC=90°-∠BEO=90°-∠AED=90°-α,∴∠COD=2∠DBC=180°-2α,∵∠AOD+∠COD=90°,∴β+180°-2α=90°,∴2α-β=90°,故选:D. 3.已知:如图,AB和CD交于⊙O内一点P,求证:PA PB=PC PD.解:证明:连接AC、BD,如图所示:∵∠CAB、∠CDB所对应圆弧都为弧BC,∴∠CAB=∠CDB,∵∠APC=∠DPB,∴△APC∽△DPB,∴ ∴PA PB=PC PD. 学生做本节练习,互相补充,教师订正答案,做最后总结。 练习是为了巩固学生所学的新知,教会学生圆周角定理及其推论,同时培养学生建模的能力。
课堂小结 圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径. 学生先发言总结本节圆周角定理,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.3.1 圆周角定理1.圆周角定理及其推论2.例1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
沪科版九年级下册数学 24.3.1圆周角定理 教学设计
课题 24.3.1圆周角定理 单元 第24单元 学科 数学 年级 九
教材分析 本节在学习了圆心角的基础上,继续学习了圆周角的概念,以及同弧所对的圆周角等于它所对圆心角的一半,并学习了两个推论:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等;半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径。
核心素养分析 本节要求掌握圆周角的概念,理解和运用圆周角定理 ,推导出2个推论:半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径”,利用圆周角定理求角和线段等元素,培养了学生推理和计算的能力,同时锻炼了学生几何直观的素养。
学习目标 1.理解圆周角的概念,理解和运用圆周角定理解几何问题2.掌握半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径
重点 理解圆周角的概念,理解和运用圆周角定理解几何问题
难点 掌握半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是直径
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 经过三点A,B ,C,可以确定一个圆吗 不在同一直线上的三个点确定一个圆.三角形的外心到三角形的三个顶点距离相等,即OA=OB=OC 回顾上节的内容,以培养学生温顾知识,大胆发言的良好习惯。 回顾上节知识,导入本节新课,圆的重要一个内容,圆周角定理。
讲授新课 如图24-33,△ABC内接于⊙O,这时∠A的顶点在圆上,∠A的两边AB, AC分别与圆还有另一个公共点。顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角。两个条件必须同时具备,缺一不可圆O中圆周角有哪几个?∠A、∠B和∠C下列图中哪个是圆周角?图(2)是圆周角探究如图24-34 ,若△ABC是等边三角形,⊙O是其外接圆,∠BAC 与∠BOC有什么关系呢?证明:∵△ABC是等边三角形∴∠BAC =∠ABC =∠BCA = 60°,又∵∠BOC =∠AOC =∠AOB =120°,∴∠BAC = ∠BOC任意画一个⊙O及其内接△ABC,用量角器量,∠BAC及∠BOC有什么样关系 一个圆周角的大小与它所对弧上的圆心角有关;前者是后者的二分之一。 以⊙O上任一点A为顶点的圆周角有无数多个,按圆心与圆周角的位置关系,存在下面三种情况,如图24-35.圆心在角的一边上 圆心在角的内部 圆心在角的外部(1)圆心在角的一边上证明:连接OC,∵△OAC是等腰三角形,∴∠A=∠OCA.∴∠BOC=∠A+∠OCA =2∠A即∠A=∠BOC.(2)圆心在角的内部证明:连接AO并延长,交⊙O于点D, 连接OB, OC,∵∠BAC =∠DAC+∠DAB∴∠BAC= ∠DOC+ ∠DOB = ∠BOC.(3)圆心在角的外部证明:连接AO并延长,交⊙O于点D, 连接OB, OC 有∠BAC= ∠DAC -∠DAB =∠DOC-∠DOB =∠COB .圆周角定理一条弧所对的圆周角等于它所对圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等(图24-36).证明:如图,连接AO,BO,∵∠C ,∠C ,∠C 所对弧上的圆心角均为∠AOB.由圆周角定理可得∠C =∠C =∠C =∠AOB.图24-36 图24-37推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径(图24-37).证明:∵A、O、B在一条直线上,∴∠AOB=180°由圆周角定理得 ∠C =∠C =∠C =180°÷2 = 90°.即直径所对的圆周角是直角,同理,90°的圆周角所对的弦AB是直径。例1 如图24-38,AB为⊙O的直径,弦CD交AB于点P,∠ACD =60°,∠ADC =70° ,求∠APC的度数.分析:∠APC等于圆周角∠BAD与∠ADC之和.解:连接BC,则∠ACB =90°,∠DCB = ∠ACB -∠ACD = 90°-60° =30°又∠BAD =∠DCB = 30°,∠APC = ∠BAD +∠ADC =30° +70°=100°. 熟悉圆周角定义,学生独立思考、小组合作讨论,发表自己的见解,大胆建议,学会倾听别的同学的意见。学生思考 从3个角度熟悉证明圆周角与圆心角的关系。理解圆周角定理的2个推论。 理解概念,帮助学生判定圆周角。巩固圆周角的概念 掌握定理的推导和证明过程。理解运用圆周角的推论。
课堂练习 1、如图,△ABC的顶点A,B在⊙O上,点C在⊙O外(O,C在AB同侧),∠AOB=98°,则∠C的度数可能是( )A. 48° B. 49° C. 50° D. 51°解:设AC与⊙O相交于点D,连接BD,∵∠AOB=98°,∴∠ADB= ∠AOB=49°,∵∠ADB是△BCD的一个外角,∴∠C<∠ADB,∴∠C的度数可能是:48°,故选:A.如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,点C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )A. 3α+β=180° B. 2α+β=180°C. 3α-β=90° D. 2α-β=90°解:∵OA⊥BC,∴∠AOB=∠AOC=90°,∴∠DBC=90°-∠BEO=90°-∠AED=90°-α,∴∠COD=2∠DBC=180°-2α,∵∠AOD+∠COD=90°,∴β+180°-2α=90°,∴2α-β=90°,故选:D. 3.已知:如图,AB和CD交于⊙O内一点P,求证:PA PB=PC PD.解:证明:连接AC、BD,如图所示:∵∠CAB、∠CDB所对应圆弧都为弧BC,∴∠CAB=∠CDB,∵∠APC=∠DPB,∴△APC∽△DPB,∴ ∴PA PB=PC PD. 学生做本节练习,互相补充,教师订正答案,做最后总结。 练习是为了巩固学生所学的新知,教会学生圆周角定理及其推论,同时培养学生建模的能力。
课堂小结 圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径. 学生先发言总结本节圆周角定理,在教师的引导下总结归纳。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题:24.3.1 圆周角定理1.圆周角定理及其推论2.例1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
