中垾初中§17.1《勾股定理》检测题(有答案)
文档属性
| 名称 | 中垾初中§17.1《勾股定理》检测题(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 91.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-08 14:38:28 | ||
图片预览

文档简介
中垾初中§17.1《勾股定理》检测题
一、选择题(每小题3分,共30分) 姓名 成绩
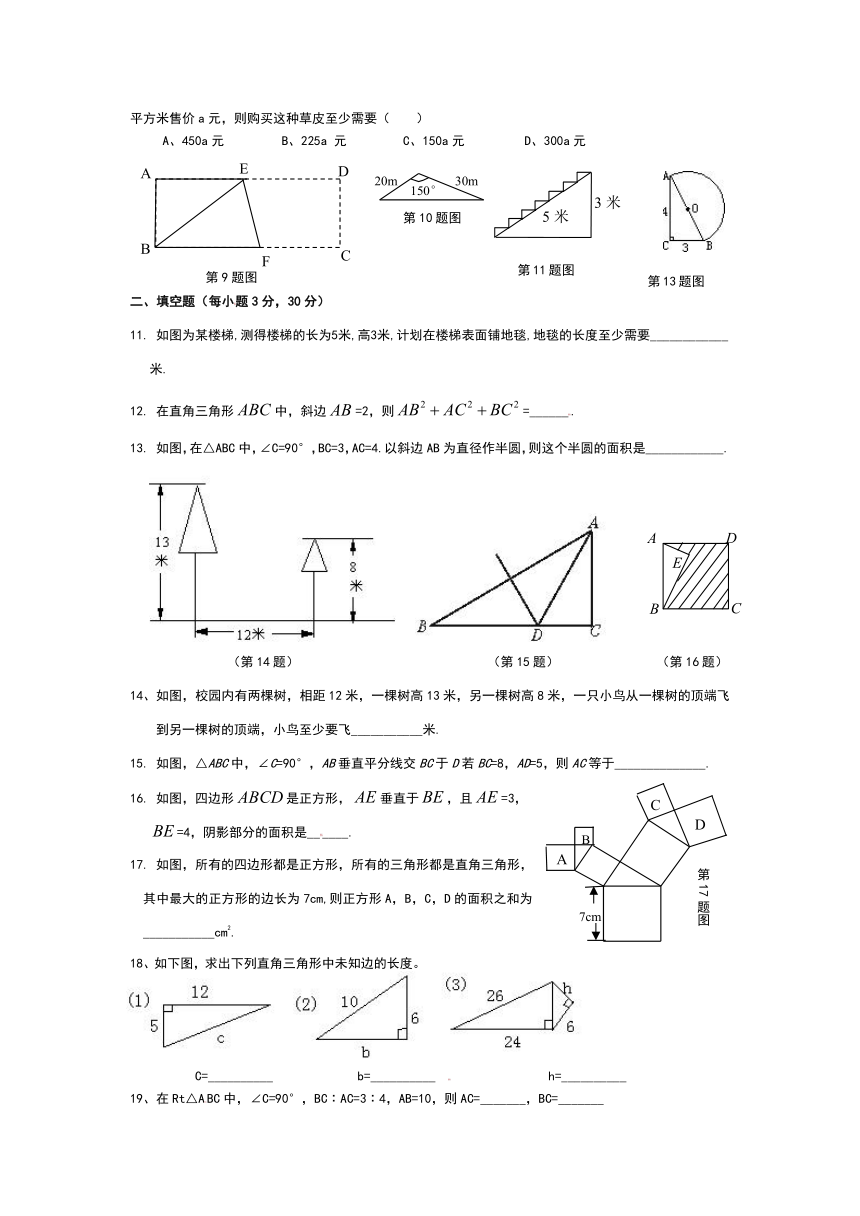
1、直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长
(A)4 cm (B)8 cm (C)10 cm (D)12 cm
2、已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
(A)25 (B)14 (C)7 (D)7或25
3、等腰三角形的腰长为10,底长为12,则其底边上的高为( )
(A)13 (B)8 (C)25 (D)64
4、 如下图五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
5. 如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
(A) 25 (B) 12.5 (C) 9 (D) 8.5
6、如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为( ).
(A)12 (B)7 (C)5 (D)13
7、一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为 ( )
A、13 B、5 C、13或5 D、无法确定
8、如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,则AC=( )
A、6 B、 C、 D、4
9、已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm2
10、某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A、450a元 B、225a 元 C、150a元 D、300a元
二、填空题(每小题3分,30分)
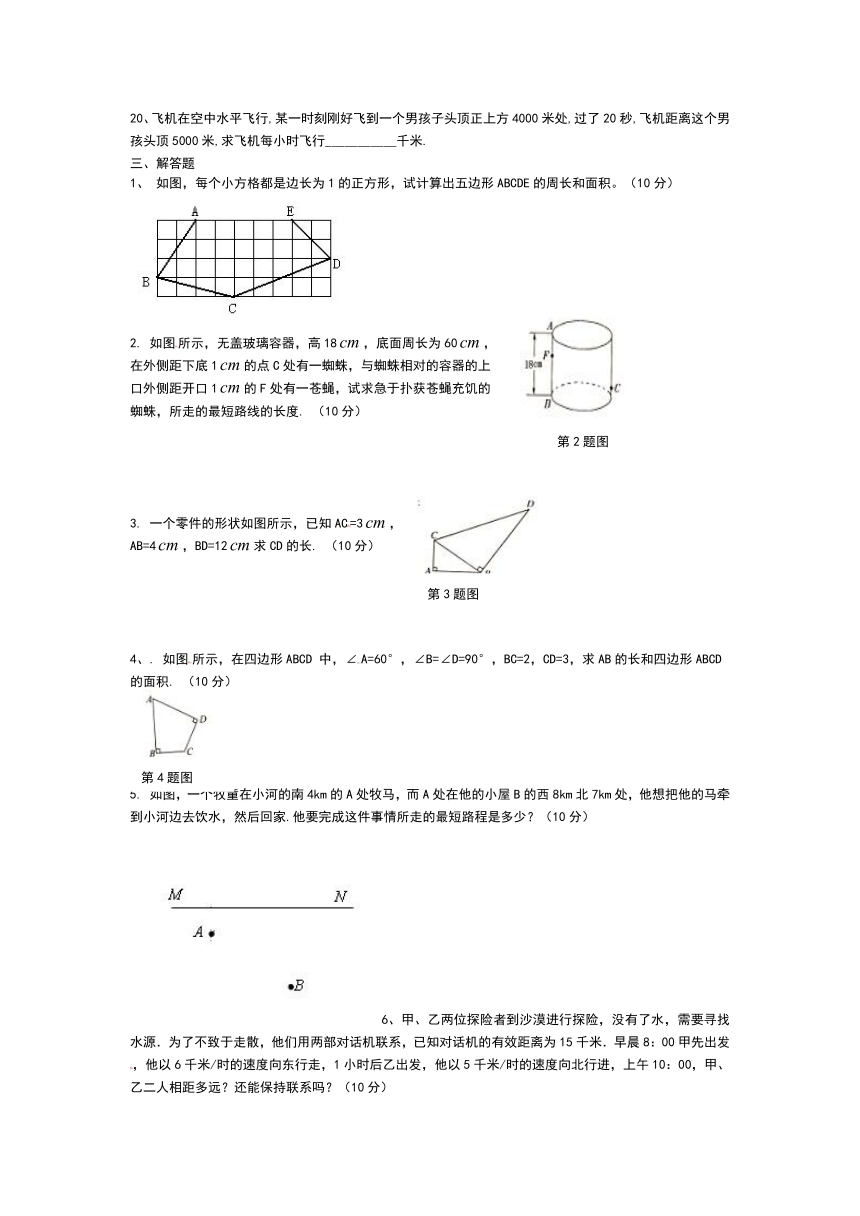
11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.
12. 在直角三角形中,斜边=2,则=______.
13. 如图,在△ABC中,∠C=90°,BC=3,AC=4.以斜边AB为直径作半圆,则这个半圆的面积是____________.
(第14题) (第15题) (第16题)
14、如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞___________米.
15. 如图,△ABC中,∠C=90°,AB垂直平分线交BC于D若BC=8,AD=5,则AC等于______________.
16. 如图,四边形是正方形,垂直于,且=3,=4,阴影部分的面积是______.
17. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2.
18、如下图,求出下列直角三角形中未知边的长度。
C=__________ b=__________ h=__________
19、在Rt△ABC中,∠C=90°,BC∶AC=3∶4,AB=10,则AC=_______,BC=_______
20、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行___________千米.
三、解答题
如图,每个小方格都是边长为1的正方形,试计算出五边形ABCDE的周长和面积。(10分)
2. 如图所示,无盖玻璃容器,高18,底面周长为60,
在外侧距下底1的点C处有一蜘蛛,与蜘蛛相对的容器的上
口外侧距开口1的F处有一苍蝇,试求急于扑获苍蝇充饥的
蜘蛛,所走的最短路线的长度. (10分)
3. 一个零件的形状如图所示,已知AC=3,
AB=4,BD=12求CD的长. (10分)
4、. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长和四边形ABCD的面积. (10分)
5. 如图,一个牧童在小河的南4km的A处牧马,而A处在他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?(10分)
6、甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?(10分)
7、某校要把一块形状是直角三角形的废地开发为生物园.如图所示,∠ACB=90°,AC=80m,BC=60m.若线段CD为一条水渠,且D在边AB上,已知水渠的造价是10元/米,则D点在距A点多远处时此水渠的造价最低?最低造价是多少?在图上标出D点.(10分)
9.如图,某沿海开放城市A接到台风警报,在该市正南方向100km的B处有一台风中心,沿BC方向以20km/h的速度向D移动,已知城市A到BC的距离AD=60km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?(10分)
8、在△ABC中,AB=AC,D是BC延长线上的点,求证:(10分)
参考答案
一、选择题1.(C);2.(D);3.(B);4.(C);5.(B);6.(D);7.(C);8.(B);9.(A);10.(C);
二、填空题11.7;12.8;13. ;14.13: 15. 4;16.19;17.49;18.13:8:8;19.8:6.20.540
三、解答题1、略 2. 解:将曲线沿AB展开,如图所示,过点C作CE⊥AB于E.
在R,EF=18-1-1=16(),CE=,
由勾股定理,得CF=
3. 解:在直角三角形ABC中,根据勾股定理,得
在直角三角形CBD中,根据勾股定理,得CD2=BC2+BD2=25+122=169,所以CD=13.
4. 解:延长BC、AD交于点E.(如图所示)
∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8,
设AB=,则AE=2,由勾股定理。得
面积为
5. 如图,作出A点关于MN的对称点A′,连接A′B交MN于点P,则A′B就是最短路线. 在Rt△A′DB中,由勾股定理求得A′B=17km
6. 解:如图,甲从上午8:00到上午10:00一共走了2小时,
走了12千米,即OA=12.
乙从上午9:00到上午10:00一共走了1小时,
走了5千米,即OB=5.在Rt△OAB中,AB2=122十52=169,∴AB=13,
因此,上午10:00时,甲、乙两人相距13千米.∵15>13, ∴甲、乙两人还能保持联系.
7.过C作CD⊥AB于D,由勾股定理,得AB=100m.
由面积,得CD=48.瑞在直角三角形ADC中利用勾股定理,得.故造价为元.答:D点在距A点64m处,此时水渠的造价最低,最低造价为480元.
8.4小时,2.5小时.
9.证明过点A作AE⊥BD于E,易得
在Rt△AED, Rt△ABE,中由勾股定理
即
E
A
B
C
D
第5题
第6题
第8题
150°
20m
30m
第10题图
A
B
E
F
D
C
第9题图
第11题图
第13题图
A
B
C
D
第17题图
7cm
第2题图
第3题图
第4题图
A
B
C
D
第8题图
A
B
D
P
N
A′
M
第5题图
O
A
B
一、选择题(每小题3分,共30分) 姓名 成绩
1、直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长
(A)4 cm (B)8 cm (C)10 cm (D)12 cm
2、已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
(A)25 (B)14 (C)7 (D)7或25
3、等腰三角形的腰长为10,底长为12,则其底边上的高为( )
(A)13 (B)8 (C)25 (D)64
4、 如下图五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
5. 如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
(A) 25 (B) 12.5 (C) 9 (D) 8.5
6、如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为( ).
(A)12 (B)7 (C)5 (D)13
7、一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为 ( )
A、13 B、5 C、13或5 D、无法确定
8、如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,则AC=( )
A、6 B、 C、 D、4
9、已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm2
10、某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A、450a元 B、225a 元 C、150a元 D、300a元
二、填空题(每小题3分,30分)
11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.
12. 在直角三角形中,斜边=2,则=______.
13. 如图,在△ABC中,∠C=90°,BC=3,AC=4.以斜边AB为直径作半圆,则这个半圆的面积是____________.
(第14题) (第15题) (第16题)
14、如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞___________米.
15. 如图,△ABC中,∠C=90°,AB垂直平分线交BC于D若BC=8,AD=5,则AC等于______________.
16. 如图,四边形是正方形,垂直于,且=3,=4,阴影部分的面积是______.
17. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2.
18、如下图,求出下列直角三角形中未知边的长度。
C=__________ b=__________ h=__________
19、在Rt△ABC中,∠C=90°,BC∶AC=3∶4,AB=10,则AC=_______,BC=_______
20、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行___________千米.
三、解答题
如图,每个小方格都是边长为1的正方形,试计算出五边形ABCDE的周长和面积。(10分)
2. 如图所示,无盖玻璃容器,高18,底面周长为60,
在外侧距下底1的点C处有一蜘蛛,与蜘蛛相对的容器的上
口外侧距开口1的F处有一苍蝇,试求急于扑获苍蝇充饥的
蜘蛛,所走的最短路线的长度. (10分)
3. 一个零件的形状如图所示,已知AC=3,
AB=4,BD=12求CD的长. (10分)
4、. 如图所示,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长和四边形ABCD的面积. (10分)
5. 如图,一个牧童在小河的南4km的A处牧马,而A处在他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?(10分)
6、甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?(10分)
7、某校要把一块形状是直角三角形的废地开发为生物园.如图所示,∠ACB=90°,AC=80m,BC=60m.若线段CD为一条水渠,且D在边AB上,已知水渠的造价是10元/米,则D点在距A点多远处时此水渠的造价最低?最低造价是多少?在图上标出D点.(10分)
9.如图,某沿海开放城市A接到台风警报,在该市正南方向100km的B处有一台风中心,沿BC方向以20km/h的速度向D移动,已知城市A到BC的距离AD=60km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?(10分)
8、在△ABC中,AB=AC,D是BC延长线上的点,求证:(10分)
参考答案
一、选择题1.(C);2.(D);3.(B);4.(C);5.(B);6.(D);7.(C);8.(B);9.(A);10.(C);
二、填空题11.7;12.8;13. ;14.13: 15. 4;16.19;17.49;18.13:8:8;19.8:6.20.540
三、解答题1、略 2. 解:将曲线沿AB展开,如图所示,过点C作CE⊥AB于E.
在R,EF=18-1-1=16(),CE=,
由勾股定理,得CF=
3. 解:在直角三角形ABC中,根据勾股定理,得
在直角三角形CBD中,根据勾股定理,得CD2=BC2+BD2=25+122=169,所以CD=13.
4. 解:延长BC、AD交于点E.(如图所示)
∵∠B=90°,∠A=60°,∴∠E=30°又∵CD=3,∴CE=6,∴BE=8,
设AB=,则AE=2,由勾股定理。得
面积为
5. 如图,作出A点关于MN的对称点A′,连接A′B交MN于点P,则A′B就是最短路线. 在Rt△A′DB中,由勾股定理求得A′B=17km
6. 解:如图,甲从上午8:00到上午10:00一共走了2小时,
走了12千米,即OA=12.
乙从上午9:00到上午10:00一共走了1小时,
走了5千米,即OB=5.在Rt△OAB中,AB2=122十52=169,∴AB=13,
因此,上午10:00时,甲、乙两人相距13千米.∵15>13, ∴甲、乙两人还能保持联系.
7.过C作CD⊥AB于D,由勾股定理,得AB=100m.
由面积,得CD=48.瑞在直角三角形ADC中利用勾股定理,得.故造价为元.答:D点在距A点64m处,此时水渠的造价最低,最低造价为480元.
8.4小时,2.5小时.
9.证明过点A作AE⊥BD于E,易得
在Rt△AED, Rt△ABE,中由勾股定理
即
E
A
B
C
D
第5题
第6题
第8题
150°
20m
30m
第10题图
A
B
E
F
D
C
第9题图
第11题图
第13题图
A
B
C
D
第17题图
7cm
第2题图
第3题图
第4题图
A
B
C
D
第8题图
A
B
D
P
N
A′
M
第5题图
O
A
B
