小学数学苏教版五年级下列方程解实际问题练习 课件(共21张PPT)
文档属性
| 名称 | 小学数学苏教版五年级下列方程解实际问题练习 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 15:21:30 | ||
图片预览








文档简介
(共21张PPT)
列方程解实际问题练习
苏教版义务教育教科书 数学 五年级下册
练习解稍复杂方程
0.7x+0.3x=9
2x+15×2=48
2x-2×0.3=8
6.6x-5x=64
练习解稍复杂方程
0.7x+0.3x=9
2x+15×2=48
2x-2×0.3=8
6.6x-5x=64
0.7x+0.3x=9
6.6x-5x=64
ax±bx=c
2x-2×0.3=8
2x+15×2=48
ax±b×c=d
练习解稍复杂方程
0.7x+0.3x=9
6.6x-5x=64
解:x=9
解:1.6x
x=40
=64
把x=9带入原方程
右边=9
左边=右边
左边=0.7×9+0.3×9=6.3+2.7=9
x=9是原方程的解
练习解稍复杂方程
0.7x+0.3x=9
6.6x-5x=64
解:x=9
解:1.6x
x=40
=64
2x-2×0.3=8
2x+15×2=48
解:2x-0.6=8
2x=8.6
x=4.3
解:2x+30=48
2x=18
x=9
练习解稍复杂方程
0.7x+0.3x=9
6.6x-5x=64
解:x=9
解:1.6x
x=40
=64
2x-2×0.3=8
2x+15×2=48
解:2x-0.6=8
2x=8.6
x=4.3
解:2x+30=48
2x=18
x=9
列方程解决实际问题
天鹅的只数+丹顶鹤的只数=一共的只数
解:设丹顶鹤有x只,天鹅有2.2x只。
x+2.2x=960
3.2x=960
x=300
2.2x=2.2×300=660
检验:(1)300+660=960(只)
(2)660÷300=2.2
答:丹顶鹤有300只,天鹅有660只。
列方程解决实际问题
(1)分析题意,寻找等量关系。
(2)设未知数,列方程。
(3)解方程,检验,写答句。
列方程解决实际问题
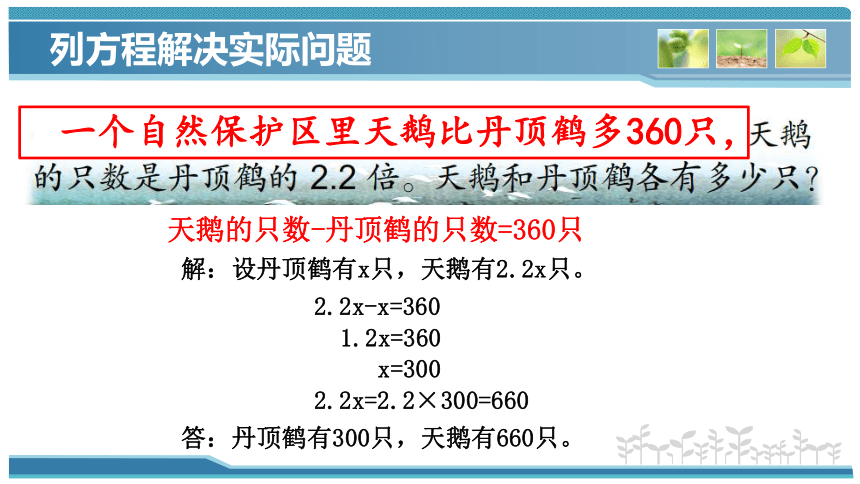
一个自然保护区里天鹅比丹顶鹤多360只,
天鹅的只数-丹顶鹤的只数=360只
解:设丹顶鹤有x只,天鹅有2.2x只。
2.2x-x=360
1.2x=360
x=300
2.2x=2.2×300=660
答:丹顶鹤有300只,天鹅有660只。
列方程解决实际问题
和倍问题
差倍问题
解:设丹顶鹤有x只,天鹅有2.2x只。
天鹅的只数+丹顶鹤的只数=一共的只数
天鹅的只数-丹顶鹤的只数=360只
列方程解决实际问题
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从
上海和南京同时相对开出,轿车的速度是118.4千米/时,大客车的
速度是110千米/时。经过几小时两车在途中相遇?
相遇问题
(用计算器计算)
轿车行驶的路程+大客车行驶的路程=总路程
解:设经过x小时两车在途中相遇。
118.4x+110x=274.08
228.4x=274.08
x=1.2
答:经过1.2小时两车在途中相遇。
速度和×时间=总路程
解:设经过x小时两车在途中相遇。
(118.4+110)x=274.08
228.4x=274.08
x=1.2
答:经过1.2小时两车在途中相遇。
列方程解决实际问题
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从
上海和南京同时相对开出,轿车的速度是118.4千米/时,大客车的
速度是110千米/时。经过1.2小时两车在途中相遇。
?千米
?千米/时
?千米/时
列方程解决实际问题
一辆轿车和一辆大客车分别从上海和南京同时相对开出,轿车的速度是118.4千米/时,大客车的速度是110千米/时。经过1.2小时两车在途中相遇。沪宁高速公路全长大约多少千米?
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从上海和南京同时相对开出,大客车的速度是110千米/时。经过1.2小时两车在途中相遇。轿车的速度是多少千米/时?
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从上海和南京同时相对开出,轿车的速度是118.4千米/时,经过1.2小时两车在途中相遇。大客车的速度是多少千米/时?
118.4×1.2+110×1.2
或(118.4+110)×1.2
1.2x+110×1.2=274.08 或(x+110)×1.2=274.08
解:设轿车的速度是x千米/时。
解:设大客车的速度是x千米/时。
118.4×1.2+1.2x=274.08 或(118.4+x)×1.2=274.08
算术方法
方程
轿车行驶的路程+大客车行驶的路程=总路程
速度和×时间=总路程
列方程解决实际问题
甲车行驶的路程+乙车行驶的路程=总路程
解:设乙车的速度是x千米/时。
42×2.4+2.4x=216
100.8+2.4x=216
2.4x=115.2
x=48
答:乙车的速度是48千米/时。
速度和×时间=总路程
解:设乙车的速度是x千米/时。
(42+x)×2.4=216
42+x=90
x=48
答:乙车的速度是48千米/时。
列方程解决实际问题
相对开出
相背而行
一辆车行驶的路程+另一辆行驶的路程=总路程
速度和×时间=总路程
列方程解决实际问题
上衣的价钱+裙子的价钱=总价
上衣的价钱+裙子的价钱=总价
一套衣服的钱×数量=总价
一套衣服的钱×数量=总价
巩固练习
一辆车行驶的路程+另一辆行驶的路程=总路程
速度和×时间=总路程
上衣的价钱+裙子的价钱=总价
一套衣服的钱×数量=总价
全课小结
列方程解实际问题
方程
方程的解
化简
计算
等式的性质
找等量关系
拓展提高
甲
乙
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,相向而行。甲的
速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
拓展提高
甲
乙
甲的路程-乙的路程=跑道一圈的长度
解:设经过x分钟甲第一次追上乙。
280x-240x=400
40x=400
x=10
答:经过10分钟甲第一次追上乙。
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,相向而行。甲的
速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
速度差
(280-240)x=400
40x=400
X=10
×时间=跑道一圈的长度
再 见 !
列方程解实际问题练习
苏教版义务教育教科书 数学 五年级下册
练习解稍复杂方程
0.7x+0.3x=9
2x+15×2=48
2x-2×0.3=8
6.6x-5x=64
练习解稍复杂方程
0.7x+0.3x=9
2x+15×2=48
2x-2×0.3=8
6.6x-5x=64
0.7x+0.3x=9
6.6x-5x=64
ax±bx=c
2x-2×0.3=8
2x+15×2=48
ax±b×c=d
练习解稍复杂方程
0.7x+0.3x=9
6.6x-5x=64
解:x=9
解:1.6x
x=40
=64
把x=9带入原方程
右边=9
左边=右边
左边=0.7×9+0.3×9=6.3+2.7=9
x=9是原方程的解
练习解稍复杂方程
0.7x+0.3x=9
6.6x-5x=64
解:x=9
解:1.6x
x=40
=64
2x-2×0.3=8
2x+15×2=48
解:2x-0.6=8
2x=8.6
x=4.3
解:2x+30=48
2x=18
x=9
练习解稍复杂方程
0.7x+0.3x=9
6.6x-5x=64
解:x=9
解:1.6x
x=40
=64
2x-2×0.3=8
2x+15×2=48
解:2x-0.6=8
2x=8.6
x=4.3
解:2x+30=48
2x=18
x=9
列方程解决实际问题
天鹅的只数+丹顶鹤的只数=一共的只数
解:设丹顶鹤有x只,天鹅有2.2x只。
x+2.2x=960
3.2x=960
x=300
2.2x=2.2×300=660
检验:(1)300+660=960(只)
(2)660÷300=2.2
答:丹顶鹤有300只,天鹅有660只。
列方程解决实际问题
(1)分析题意,寻找等量关系。
(2)设未知数,列方程。
(3)解方程,检验,写答句。
列方程解决实际问题
一个自然保护区里天鹅比丹顶鹤多360只,
天鹅的只数-丹顶鹤的只数=360只
解:设丹顶鹤有x只,天鹅有2.2x只。
2.2x-x=360
1.2x=360
x=300
2.2x=2.2×300=660
答:丹顶鹤有300只,天鹅有660只。
列方程解决实际问题
和倍问题
差倍问题
解:设丹顶鹤有x只,天鹅有2.2x只。
天鹅的只数+丹顶鹤的只数=一共的只数
天鹅的只数-丹顶鹤的只数=360只
列方程解决实际问题
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从
上海和南京同时相对开出,轿车的速度是118.4千米/时,大客车的
速度是110千米/时。经过几小时两车在途中相遇?
相遇问题
(用计算器计算)
轿车行驶的路程+大客车行驶的路程=总路程
解:设经过x小时两车在途中相遇。
118.4x+110x=274.08
228.4x=274.08
x=1.2
答:经过1.2小时两车在途中相遇。
速度和×时间=总路程
解:设经过x小时两车在途中相遇。
(118.4+110)x=274.08
228.4x=274.08
x=1.2
答:经过1.2小时两车在途中相遇。
列方程解决实际问题
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从
上海和南京同时相对开出,轿车的速度是118.4千米/时,大客车的
速度是110千米/时。经过1.2小时两车在途中相遇。
?千米
?千米/时
?千米/时
列方程解决实际问题
一辆轿车和一辆大客车分别从上海和南京同时相对开出,轿车的速度是118.4千米/时,大客车的速度是110千米/时。经过1.2小时两车在途中相遇。沪宁高速公路全长大约多少千米?
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从上海和南京同时相对开出,大客车的速度是110千米/时。经过1.2小时两车在途中相遇。轿车的速度是多少千米/时?
沪宁高速公路全长大约274.08千米。一辆轿车和一辆大客车分别从上海和南京同时相对开出,轿车的速度是118.4千米/时,经过1.2小时两车在途中相遇。大客车的速度是多少千米/时?
118.4×1.2+110×1.2
或(118.4+110)×1.2
1.2x+110×1.2=274.08 或(x+110)×1.2=274.08
解:设轿车的速度是x千米/时。
解:设大客车的速度是x千米/时。
118.4×1.2+1.2x=274.08 或(118.4+x)×1.2=274.08
算术方法
方程
轿车行驶的路程+大客车行驶的路程=总路程
速度和×时间=总路程
列方程解决实际问题
甲车行驶的路程+乙车行驶的路程=总路程
解:设乙车的速度是x千米/时。
42×2.4+2.4x=216
100.8+2.4x=216
2.4x=115.2
x=48
答:乙车的速度是48千米/时。
速度和×时间=总路程
解:设乙车的速度是x千米/时。
(42+x)×2.4=216
42+x=90
x=48
答:乙车的速度是48千米/时。
列方程解决实际问题
相对开出
相背而行
一辆车行驶的路程+另一辆行驶的路程=总路程
速度和×时间=总路程
列方程解决实际问题
上衣的价钱+裙子的价钱=总价
上衣的价钱+裙子的价钱=总价
一套衣服的钱×数量=总价
一套衣服的钱×数量=总价
巩固练习
一辆车行驶的路程+另一辆行驶的路程=总路程
速度和×时间=总路程
上衣的价钱+裙子的价钱=总价
一套衣服的钱×数量=总价
全课小结
列方程解实际问题
方程
方程的解
化简
计算
等式的性质
找等量关系
拓展提高
甲
乙
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,相向而行。甲的
速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
拓展提高
甲
乙
甲的路程-乙的路程=跑道一圈的长度
解:设经过x分钟甲第一次追上乙。
280x-240x=400
40x=400
x=10
答:经过10分钟甲第一次追上乙。
甲、乙两人沿着400米的环形跑道跑步,他们同时从同一地点出发,相向而行。甲的
速度是280米/分,乙的速度是240米/分。经过多少分钟甲第一次追上乙?
速度差
(280-240)x=400
40x=400
X=10
×时间=跑道一圈的长度
再 见 !
