人教版(2023春)数学三年级下册综合与实践 我们的校园【课件】(共18张PPT)
文档属性
| 名称 | 人教版(2023春)数学三年级下册综合与实践 我们的校园【课件】(共18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 20:38:05 | ||
图片预览




文档简介
(共18张PPT)
2023春 人教数学
三年级下册
综合与实践
我们的校园
R·
三
年
册
级
下
情境导入
校园里每天都会有许多问题要用数学来解决。
创设情景,引入新课
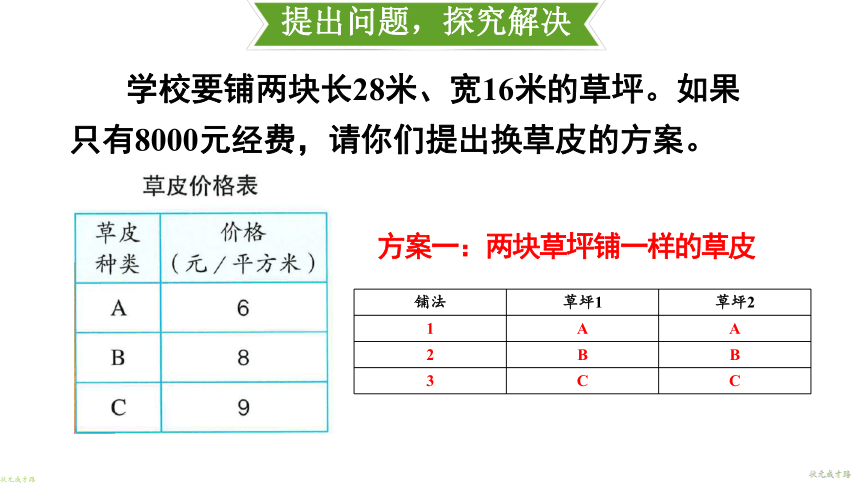
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
提出问题,探究解决
方案一:两块草坪铺一样的草皮
铺法 草坪1 草坪2
1 A A
2 B B
3 C C
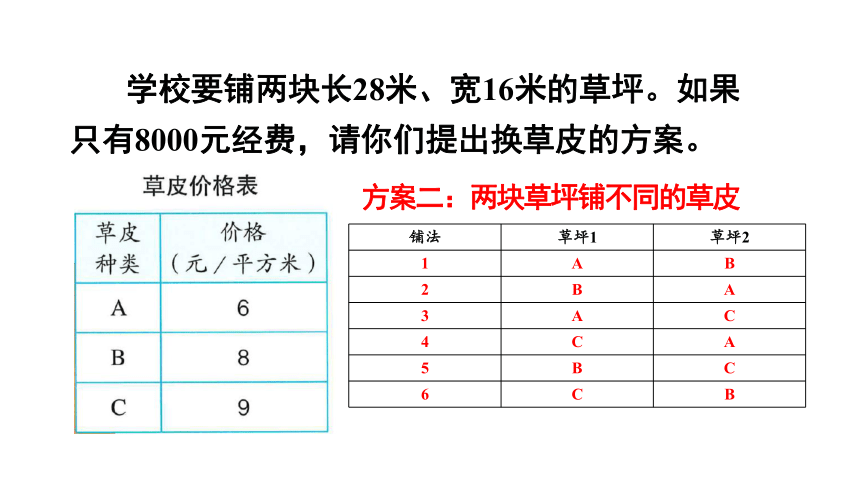
方案二:两块草坪铺不同的草皮
铺法 草坪1 草坪2
1 A B
2 B A
3 A C
4 C A
5 B C
6 C B
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
每块草坪的面积:
28×16=448(平方米)
铺法 草坪1 草坪2 费用(元)
1 A A
2 B B
3 C C
5376
7168
8064
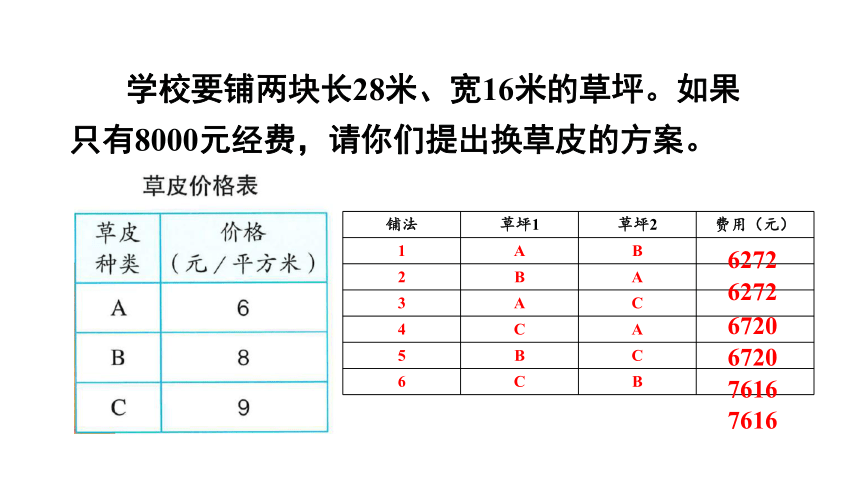
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
铺法 草坪1 草坪2 费用(元)
1 A B
2 B A
3 A C
4 C A
5 B C
6 C B
6272
6272
6720
6720
7616
7616
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
“赛程安排”
本周五下午课外活动时间,在运动场的东、西两侧举行三年级拔河比赛。请你们设计一份赛程安排。
比赛安排在15:00—16:30进行,地点在运动场的东、西两侧。
三年级有4个班,先分组比赛,胜者再进行决赛。
每场比赛要用20分钟,赛前准备10分钟。
活动建议
1.说一说:一共需要安排几场比赛?
2.想一想:怎样安排比赛时间和地点?
3.议一议:哪种设计更合理?
4.写一写:把你们组安排的赛程清晰地表示出来。
对阵 时间 地点
我们用表格的形式通知比赛的时间和地点。
还有其他的方法吗?
A组:三(1)—三(2)
B组:三(3)—三(4)
A组胜者—B组胜者
颁奖
15:10—15:30
15:10—15:30
15:40—16:00
16:10—16:20
运动场东侧
运动场西侧
运动场东侧
运动场西侧
情境导入
学校新建了两间音乐教室,要给教室地面铺上漂亮的地砖。两间音乐教室同样大,都是长18米,宽10米。如果只有15000元的费用,请你提出铺地砖的建议。
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
18×10=180(平方米)=18000(平方分米)
达标检测
有 6 种不同的铺法,需要的钱分别是:
①只铺A地砖:18000÷4×2×2=18000(元)
②只铺B地砖: 18000÷9×2×4=16000(元)
③只铺C地砖: 18000÷18×2×6=12000(元)
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
④分别铺A、B两种地砖:
18000÷4×2+18000÷9×4=17000(元)
⑤分别铺A、C两种地砖:
18000÷4×2+18000÷18×6=15000(元)
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
⑥分别铺B、C两种地砖:
18000÷9×4+18000÷18×6=14000(元)
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
建议:①两间教室都铺 C 地砖需要12000 元。
②一间教室铺 A 地砖,另一间教室铺C 地砖,需要 15000 元。
③一间教室铺 B 地砖,另一间教室铺C 地砖,需要 14000 元。
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
同学们,今天的数学课你们有哪些收获呢?
课堂小结
备选练习
学校新建了两间舞蹈教室,要给教室地面铺上地毯。
地毯类型 地毯面积 单价(元/块)
A 2平方米 20
B 4平方米 30
C 6平方米 40
两间舞蹈教室同样大,都是长24米、宽16米。
如果只有6000元的费用,请你提出铺地毯的建议。
两间舞蹈教室要铺不同类型的地毯。有多少种不同的铺法?算一算各要多少钱。
24×16=384(平方米)
有三种铺法:
①A+B 384÷2×20+384÷4×30=6720(元)
②A+C 384÷2×20+384÷6×40=6400(元)
③B+C 384÷4×30+384÷6×40=5440(元)
因为费用只有6000元,故两间教室分别铺B类地毯和C类地毯。
地毯类型 地毯面积 单价(元/块)
A 2平方米 20
B 4平方米 30
C 6平方米 40
2023春 人教数学
三年级下册
综合与实践
我们的校园
R·
三
年
册
级
下
情境导入
校园里每天都会有许多问题要用数学来解决。
创设情景,引入新课
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
提出问题,探究解决
方案一:两块草坪铺一样的草皮
铺法 草坪1 草坪2
1 A A
2 B B
3 C C
方案二:两块草坪铺不同的草皮
铺法 草坪1 草坪2
1 A B
2 B A
3 A C
4 C A
5 B C
6 C B
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
每块草坪的面积:
28×16=448(平方米)
铺法 草坪1 草坪2 费用(元)
1 A A
2 B B
3 C C
5376
7168
8064
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
铺法 草坪1 草坪2 费用(元)
1 A B
2 B A
3 A C
4 C A
5 B C
6 C B
6272
6272
6720
6720
7616
7616
学校要铺两块长28米、宽16米的草坪。如果只有8000元经费,请你们提出换草皮的方案。
“赛程安排”
本周五下午课外活动时间,在运动场的东、西两侧举行三年级拔河比赛。请你们设计一份赛程安排。
比赛安排在15:00—16:30进行,地点在运动场的东、西两侧。
三年级有4个班,先分组比赛,胜者再进行决赛。
每场比赛要用20分钟,赛前准备10分钟。
活动建议
1.说一说:一共需要安排几场比赛?
2.想一想:怎样安排比赛时间和地点?
3.议一议:哪种设计更合理?
4.写一写:把你们组安排的赛程清晰地表示出来。
对阵 时间 地点
我们用表格的形式通知比赛的时间和地点。
还有其他的方法吗?
A组:三(1)—三(2)
B组:三(3)—三(4)
A组胜者—B组胜者
颁奖
15:10—15:30
15:10—15:30
15:40—16:00
16:10—16:20
运动场东侧
运动场西侧
运动场东侧
运动场西侧
情境导入
学校新建了两间音乐教室,要给教室地面铺上漂亮的地砖。两间音乐教室同样大,都是长18米,宽10米。如果只有15000元的费用,请你提出铺地砖的建议。
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
18×10=180(平方米)=18000(平方分米)
达标检测
有 6 种不同的铺法,需要的钱分别是:
①只铺A地砖:18000÷4×2×2=18000(元)
②只铺B地砖: 18000÷9×2×4=16000(元)
③只铺C地砖: 18000÷18×2×6=12000(元)
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
④分别铺A、B两种地砖:
18000÷4×2+18000÷9×4=17000(元)
⑤分别铺A、C两种地砖:
18000÷4×2+18000÷18×6=15000(元)
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
⑥分别铺B、C两种地砖:
18000÷9×4+18000÷18×6=14000(元)
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
建议:①两间教室都铺 C 地砖需要12000 元。
②一间教室铺 A 地砖,另一间教室铺C 地砖,需要 15000 元。
③一间教室铺 B 地砖,另一间教室铺C 地砖,需要 14000 元。
地砖类型 地砖面积 单价(元/块)
A 4 平方分米 2
B 9 平方分米 4
C 18 平方分米 6
同学们,今天的数学课你们有哪些收获呢?
课堂小结
备选练习
学校新建了两间舞蹈教室,要给教室地面铺上地毯。
地毯类型 地毯面积 单价(元/块)
A 2平方米 20
B 4平方米 30
C 6平方米 40
两间舞蹈教室同样大,都是长24米、宽16米。
如果只有6000元的费用,请你提出铺地毯的建议。
两间舞蹈教室要铺不同类型的地毯。有多少种不同的铺法?算一算各要多少钱。
24×16=384(平方米)
有三种铺法:
①A+B 384÷2×20+384÷4×30=6720(元)
②A+C 384÷2×20+384÷6×40=6400(元)
③B+C 384÷4×30+384÷6×40=5440(元)
因为费用只有6000元,故两间教室分别铺B类地毯和C类地毯。
地毯类型 地毯面积 单价(元/块)
A 2平方米 20
B 4平方米 30
C 6平方米 40
