沪科版数学九年级下册25.2 第1课时 三视图的识别与画法 学案(无答案)
文档属性
| 名称 | 沪科版数学九年级下册25.2 第1课时 三视图的识别与画法 学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 19:47:35 | ||
图片预览

文档简介
25.2 三视图
第1课时 三视图的识别与画法
【学习目标】
(一)知识技能:
1.会从投影角度理解视图的概念;学会根据物体的三视图描述出几何体的基本形状。
2.会画几何体的三视图,经历探索简单的几何体的三视图的还原,进一步发展空间想象能力。
(二)数学思考:通过具体活动,积累观察,想象物体投影的经验。
(三)解决问题:会画实际生活中简单物体的三视图。
(四)情感态度:
1.培养学生自主学习与合作学习相结合的学习方式,使学生体会从生活中发现数学。
2.在应用数学解决生活中问题的过程中,品尝成功的喜悦,激发学生应用数学的热情。
【学习重点】
从投影的角度加深对三视图概念的理解。
会画简单几何体的三视图,根据三视图描述基本几何体和实物原型。
【学习难点】
对三视图概念理解的升华。
正确画出三棱柱的三视图和小零件的三视图,根据三视图想象基本几何体实物原型。
【学习过程】
【情境引入】
活动一
如图,直三棱柱的侧棱与水平投影面垂直。请与同伴一起探讨下面的问题:
以水平投影面为投影面,在正投影下,这个直棱柱的三条侧棱的投影是什么图形?
画出直三棱柱在水平投影面的正投影,得到的投影是什么图形?它与直三棱柱的底面有什么关系?
(3)这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
【自主探究】
活动二
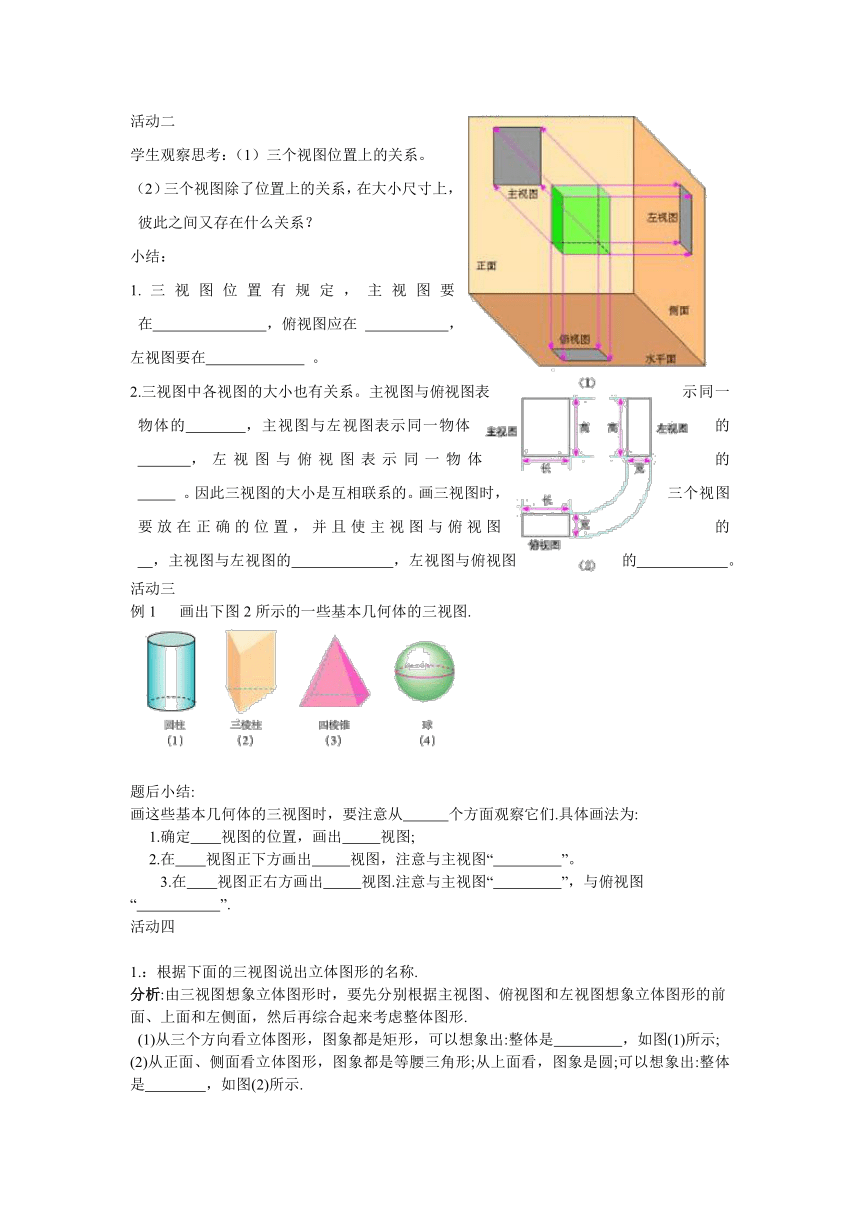
学生观察思考:(1)三个视图位置上的关系。
(2)三个视图除了位置上的关系,在大小尺寸上,彼此之间又存在什么关系?
小结:
1.三视图位置有规定,主视图要在 ,俯视图应在 ,
左视图要在 。
2.三视图中各视图的大小也有关系。主视图与俯视图表示同一物体的 ,主视图与左视图表示同一物体的 ,左视图与俯视图表示同一物体的 。因此三视图的大小是互相联系的。画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的 ,主视图与左视图的 ,左视图与俯视图的 。
活动三
例1 画出下图2所示的一些基本几何体的三视图.
题后小结:
画这些基本几何体的三视图时,要注意从 个方面观察它们.具体画法为:
1.确定 视图的位置,画出 视图;
2.在 视图正下方画出 视图,注意与主视图“ ”。
3.在 视图正右方画出 视图.注意与主视图“ ”,与俯视图“ ”.
活动四
1.:根据下面的三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
(1)从三个方向看立体图形,图象都是矩形,可以想象出:整体是 ,如图(1)所示;
(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出:整体是 ,如图(2)所示.
2.根据物体的三视图,如下图(1),描述物体的形状.
分析.由主视图可知,物体正面是正五边形,由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到。两条棱(虚线)被遮挡,由左视图知,物体的侧面是矩形的.且有一条棱〔中间的实线)可见到,综合各视图可知,物体是 形状的,如上图(2)所示.
3.画出符合下列三视图的小立方块构成的几何体。
分析:首先应由三种视图从三个方向确定分别有几层,每层有几个,每个小正方体的具体位置在哪儿?画出之后再看一是否和所给三视图保持一致
题后小结:
1、一个视图不能确定物体的空间形状,根据三视图要描述几何体或实物原型时,必须将各视图对照起来看.
2、一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。例如:正方体的主视图是正方形,但主视图是正方形的几何体有直三棱柱、长方体、圆柱等.
3、对于较复杂的物体,由三视图想象出物体的原型,应搞清三个视图之间的前后、左右、上下的对应关系.
【巩固练习】
1.画出图中的几何体的三视图。
题后小结:
画三视图时,看得见的轮廓线通常画成_______,看不见的部分通常画成_______。
2、你能画出下图中几何体的三视图吗 ?
(二)方法汇总
画基本几何体的三视图时,要注意从 个方面观察它们.具体画法为:
1.确定 视图的位置,画出 视图;
2.在 视图正下方画出 视图,注意与主视图“ ”。
3.在 视图正右方画出 视图.注意与主视图“ ”,与俯视图“ ”.
4.看得见的轮廓线通常画成_______,看不见的部分通常画成_______。
【布置作业】
第1课时 三视图的识别与画法
【学习目标】
(一)知识技能:
1.会从投影角度理解视图的概念;学会根据物体的三视图描述出几何体的基本形状。
2.会画几何体的三视图,经历探索简单的几何体的三视图的还原,进一步发展空间想象能力。
(二)数学思考:通过具体活动,积累观察,想象物体投影的经验。
(三)解决问题:会画实际生活中简单物体的三视图。
(四)情感态度:
1.培养学生自主学习与合作学习相结合的学习方式,使学生体会从生活中发现数学。
2.在应用数学解决生活中问题的过程中,品尝成功的喜悦,激发学生应用数学的热情。
【学习重点】
从投影的角度加深对三视图概念的理解。
会画简单几何体的三视图,根据三视图描述基本几何体和实物原型。
【学习难点】
对三视图概念理解的升华。
正确画出三棱柱的三视图和小零件的三视图,根据三视图想象基本几何体实物原型。
【学习过程】
【情境引入】
活动一
如图,直三棱柱的侧棱与水平投影面垂直。请与同伴一起探讨下面的问题:
以水平投影面为投影面,在正投影下,这个直棱柱的三条侧棱的投影是什么图形?
画出直三棱柱在水平投影面的正投影,得到的投影是什么图形?它与直三棱柱的底面有什么关系?
(3)这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
【自主探究】
活动二
学生观察思考:(1)三个视图位置上的关系。
(2)三个视图除了位置上的关系,在大小尺寸上,彼此之间又存在什么关系?
小结:
1.三视图位置有规定,主视图要在 ,俯视图应在 ,
左视图要在 。
2.三视图中各视图的大小也有关系。主视图与俯视图表示同一物体的 ,主视图与左视图表示同一物体的 ,左视图与俯视图表示同一物体的 。因此三视图的大小是互相联系的。画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的 ,主视图与左视图的 ,左视图与俯视图的 。
活动三
例1 画出下图2所示的一些基本几何体的三视图.
题后小结:
画这些基本几何体的三视图时,要注意从 个方面观察它们.具体画法为:
1.确定 视图的位置,画出 视图;
2.在 视图正下方画出 视图,注意与主视图“ ”。
3.在 视图正右方画出 视图.注意与主视图“ ”,与俯视图“ ”.
活动四
1.:根据下面的三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
(1)从三个方向看立体图形,图象都是矩形,可以想象出:整体是 ,如图(1)所示;
(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出:整体是 ,如图(2)所示.
2.根据物体的三视图,如下图(1),描述物体的形状.
分析.由主视图可知,物体正面是正五边形,由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到。两条棱(虚线)被遮挡,由左视图知,物体的侧面是矩形的.且有一条棱〔中间的实线)可见到,综合各视图可知,物体是 形状的,如上图(2)所示.
3.画出符合下列三视图的小立方块构成的几何体。
分析:首先应由三种视图从三个方向确定分别有几层,每层有几个,每个小正方体的具体位置在哪儿?画出之后再看一是否和所给三视图保持一致
题后小结:
1、一个视图不能确定物体的空间形状,根据三视图要描述几何体或实物原型时,必须将各视图对照起来看.
2、一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。例如:正方体的主视图是正方形,但主视图是正方形的几何体有直三棱柱、长方体、圆柱等.
3、对于较复杂的物体,由三视图想象出物体的原型,应搞清三个视图之间的前后、左右、上下的对应关系.
【巩固练习】
1.画出图中的几何体的三视图。
题后小结:
画三视图时,看得见的轮廓线通常画成_______,看不见的部分通常画成_______。
2、你能画出下图中几何体的三视图吗 ?
(二)方法汇总
画基本几何体的三视图时,要注意从 个方面观察它们.具体画法为:
1.确定 视图的位置,画出 视图;
2.在 视图正下方画出 视图,注意与主视图“ ”。
3.在 视图正右方画出 视图.注意与主视图“ ”,与俯视图“ ”.
4.看得见的轮廓线通常画成_______,看不见的部分通常画成_______。
【布置作业】
