沪科版七年级数学下册第6章 实数 小结.评价 教学课件(共20张PPT)
文档属性
| 名称 | 沪科版七年级数学下册第6章 实数 小结.评价 教学课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 625.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 19:56:50 | ||
图片预览





文档简介
(共20张PPT)
第6章 实数
小结 评价
学习目标
1.通过复习,区分并会求数的平方根、算术平方根和立方根.
2.了解无理数、实数的意义,并会进行分类,会用计算器进行数的加、减、乘、除、乘方及开方运算.
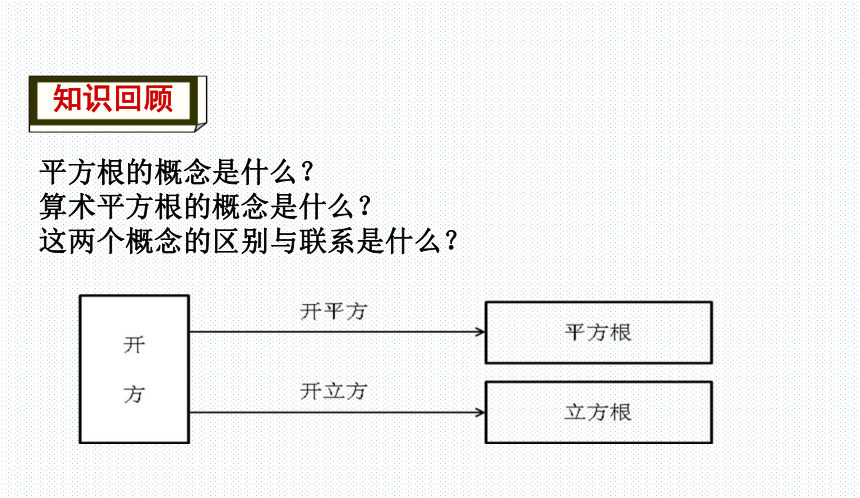
平方根的概念是什么?
算术平方根的概念是什么?
这两个概念的区别与联系是什么?
知识回顾
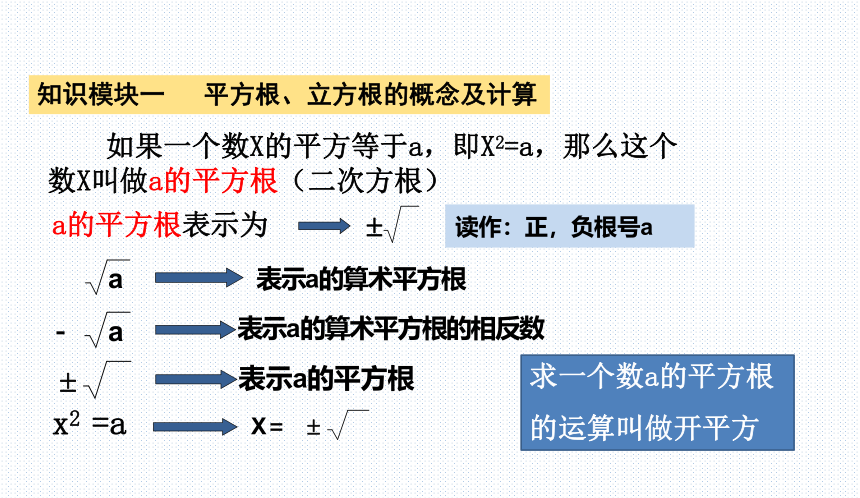
一般地,如果一个正数 x 的平方等于a(x2=a),那么这个正数 x 就叫做 a 的
算术平方根
a 的算术平方根记作
读作
“ 根号a ”
根号
被开方数
规定:0的算术平方根等于0
如102 = 100
则100的算术平方根
自学互研
如果一个数X的平方等于a,即X2=a,那么这个
数X叫做a的平方根(二次方根)
a的平方根表示为
x2 =a
求一个数a的平方根
的运算叫做开平方
知识模块一 平方根、立方根的概念及计算
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
平方根的性质
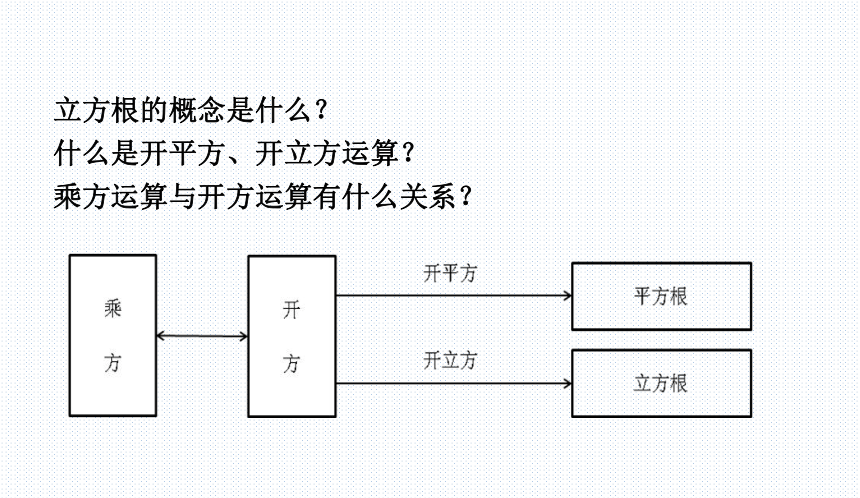
立方根的概念是什么?
什么是开平方、开立方运算?
乘方运算与开方运算有什么关系?
正数有立方根吗?如果有,有几个
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
立方根的特征
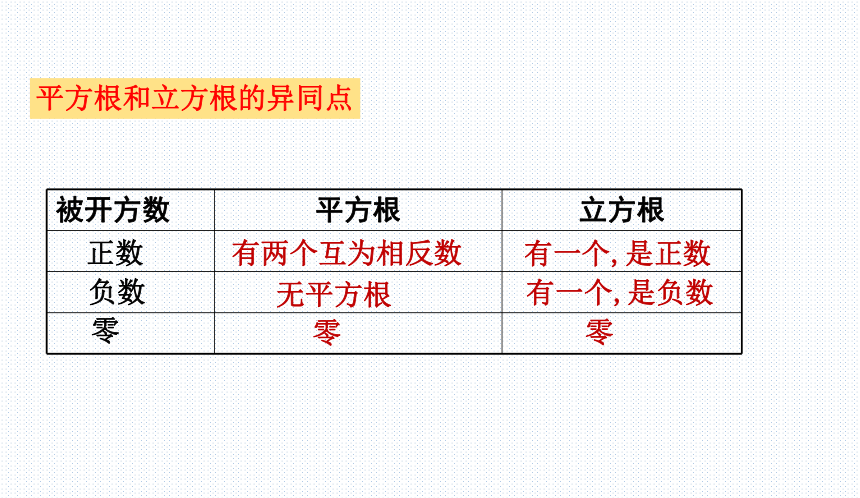
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
平方根和立方根的异同点
=
无理数和有理数的区别是什么?
无理数不能表示成两个整数之比,
是无限不循环小数.
有理数是能够表示成两个整数之比的数,是整数或有限小数.
实数由哪些数组成?
知识模块二 实数的有关概念及性质应用
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
有限小数及无限循环小数
无限不循环小数
一般有三种情况
实数还可分为正实数、
0、负实数。
数的范围是怎样从正整数逐步扩充到实数的?随着数的不断扩充,数的运算有什么发展?加法与乘法的运算律始终保持不变吗?
运算:加、减、乘、除、乘方、开方.
运算律:加法交换律、加法结合率、乘法交换律、乘法结合律、乘法分配律.
实
数
运
算
实数与数轴上的点有什么关系?
实数与数轴上的点是“一一对应”的.
数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
比较大小
1.(1) 的倒数是 ;
(2) -2的绝对值是 ;
当堂练习
2.已知实数a、b在数轴上对应点的位置如图;
化简:|a-b|+
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+ =(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
b a o
x
3.若
求 的值。
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-43,b=34
∴a2003b2004=(-4/3)2003·(3/4)2004=-34
4.下列各组数,互为相反数的( )
A.2和 B.(-1) 和1 C.-1和(-1) D.2和|-2|
C
1.注意平方根与算术平方根的区别与关系。要求一个的平方根或算术平方根,须将这个数先进行化简或计算。
2.什么是实数?
3.已知条件是含有字母的二次根式,要注意隐含的条件,因为 中 ,一般遇到 可转化为 去处理。
知识梳理
第6章 实数
小结 评价
学习目标
1.通过复习,区分并会求数的平方根、算术平方根和立方根.
2.了解无理数、实数的意义,并会进行分类,会用计算器进行数的加、减、乘、除、乘方及开方运算.
平方根的概念是什么?
算术平方根的概念是什么?
这两个概念的区别与联系是什么?
知识回顾
一般地,如果一个正数 x 的平方等于a(x2=a),那么这个正数 x 就叫做 a 的
算术平方根
a 的算术平方根记作
读作
“ 根号a ”
根号
被开方数
规定:0的算术平方根等于0
如102 = 100
则100的算术平方根
自学互研
如果一个数X的平方等于a,即X2=a,那么这个
数X叫做a的平方根(二次方根)
a的平方根表示为
x2 =a
求一个数a的平方根
的运算叫做开平方
知识模块一 平方根、立方根的概念及计算
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
平方根的性质
立方根的概念是什么?
什么是开平方、开立方运算?
乘方运算与开方运算有什么关系?
正数有立方根吗?如果有,有几个
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
立方根的特征
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
平方根和立方根的异同点
=
无理数和有理数的区别是什么?
无理数不能表示成两个整数之比,
是无限不循环小数.
有理数是能够表示成两个整数之比的数,是整数或有限小数.
实数由哪些数组成?
知识模块二 实数的有关概念及性质应用
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
有限小数及无限循环小数
无限不循环小数
一般有三种情况
实数还可分为正实数、
0、负实数。
数的范围是怎样从正整数逐步扩充到实数的?随着数的不断扩充,数的运算有什么发展?加法与乘法的运算律始终保持不变吗?
运算:加、减、乘、除、乘方、开方.
运算律:加法交换律、加法结合率、乘法交换律、乘法结合律、乘法分配律.
实
数
运
算
实数与数轴上的点有什么关系?
实数与数轴上的点是“一一对应”的.
数轴上的右边点表示的数总是大于左边点表示的数,正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
比较大小
1.(1) 的倒数是 ;
(2) -2的绝对值是 ;
当堂练习
2.已知实数a、b在数轴上对应点的位置如图;
化简:|a-b|+
解:由图知:b<a<0,∴a-b>0,a+b<0.
∴|a-b|+ =(a-b)+|a+b|
=a-b+[-(a+b)]
=a-b-a-b
=-2b.
b a o
x
3.若
求 的值。
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a=-43,b=34
∴a2003b2004=(-4/3)2003·(3/4)2004=-34
4.下列各组数,互为相反数的( )
A.2和 B.(-1) 和1 C.-1和(-1) D.2和|-2|
C
1.注意平方根与算术平方根的区别与关系。要求一个的平方根或算术平方根,须将这个数先进行化简或计算。
2.什么是实数?
3.已知条件是含有字母的二次根式,要注意隐含的条件,因为 中 ,一般遇到 可转化为 去处理。
知识梳理
