沪科版数学九年级下册25.2 三视图导学课件(共39张PPT)
文档属性
| 名称 | 沪科版数学九年级下册25.2 三视图导学课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 20:16:54 | ||
图片预览










文档简介
(共39张PPT)
25.2 三视图
第二十五章 投影与视图
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
三视图及其相关概念
画几何体的三视图
棱柱及其相关概念
由三视图确定几何体
感悟新知
知识点
三视图及其相关概念
1
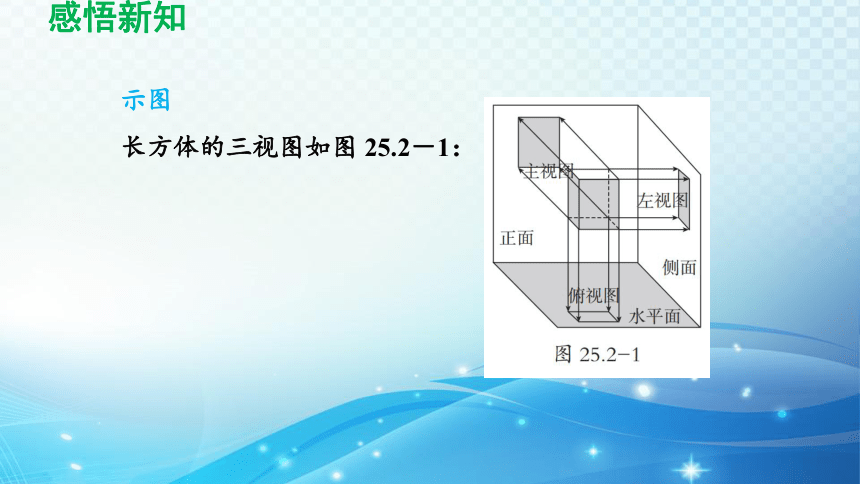
1.正面、水平面、侧面 用三个互相垂直的平面作为投影面,其中正对着我们的面叫做正面,下方的面叫做水平面,右边的面叫做侧面 .
感悟新知
三视图 对一个几何体在三个投影面内进行正投影,得到的三个平面图形组成这个几何体的三视图,其中:
(1) 主视图: 自几何体的前方向后投射,在正面投影面上得到的视图称为主视图;
(2)俯视图:自几何体的上方向下投射,在水平投影面上得到的视图称为俯视图;
(3)左视图:自几何体的左侧向右投射,在侧面投影面上得到的视图称为左视图 .
感悟新知
3. 三视图与正投影的关系 某些物体的三视图实际上是该物体在一定条件下所形成的正投影,某些物体的主视图、左视图、俯视图可以看成一束平行光线分别从物体的正面、左面、上面照射,在垂直于这些光线的平面上所形成的正投影 .
感悟新知
速记口诀
视图来源正投影,三个方向实物成,
从前向后主视图,从上向下俯视图,
从左向右左视图,统称物体三视图 .
感悟新知
示图
长方体的三视图如图 25.2-1:
感悟新知
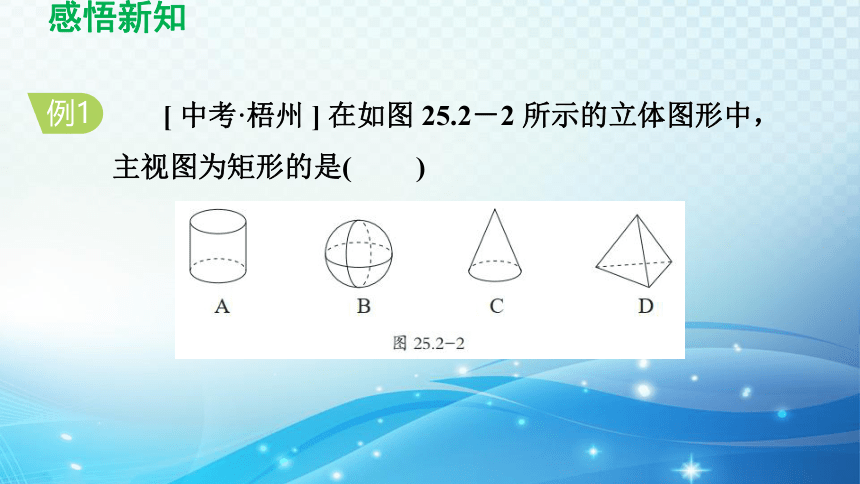
[ 中考·梧州 ] 在如图 25.2-2 所示的立体图形中,主视图为矩形的是( )
例1
感悟新知
解:A. 圆柱的主视图是矩形,故本选项符合题意;
B. 球的主视图是圆,故本选项不符合题意;
C. 圆锥的主视图是等腰三角形,故本选项不符合题意;
D. 三棱锥的主视图是三角形,故本选项不符合题意.
解题秘方:根据主视图是从几何体正面看所得到的图形,分别得出四个几何体的主视图,即可解答.
答案:A
感悟新知
方法点拨
本题考查了简单几何体的主视图,注意主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
感悟新知
知识点
画几何体的三视图
2
1. 三视图之间的关系
(1)位置关系: 主视图在左上方,主视图的正下方是俯视图,主视图的正右方是左视图 . 主视图反映几何体的长与高,俯视图反映几何体的长与宽,左视图反映几何体的高与宽 .
感悟新知
(2) 大小关系:三视图之间的大小是相互联系的 . 主视图的长与俯视图的长对正,主视图的高与左视图的高平齐,俯视图的宽与左视图的宽相等 .
感悟新知
速记口诀
视图位置要摆明,画图规则要记清.
主俯视图长对正,左俯视图宽相等.
主左视图高平齐,实线虚线应分清 .
感悟新知
2. 三视图的画法:
(1)确定主视图的位置, 画出主视图;
(2)在主视图的正下方画出俯视图,并且主视图与俯视图的长对正;
感悟新知
(3)在主视图的正右方画出左视图,与主视图的高平齐,与俯视图的宽相等(可简述为长对正,高平齐,宽相等) . 图 25.2-3 ①中的几何体的三视图如图 25.2-3 ②所示 .
感悟新知
3. 画三视图的规定 画三视图时,看得见的部分的轮廓线画成实线,因被其他部分遮挡而看不见的部分的轮廓线画成虚线 .
感悟新知
一种机器上有一个零件叫燕尾槽(如图 25.2-4),请画出它的三视图 .
例2
感悟新知
解:这个燕尾槽的三视图如图 25.2-5 所示 .
感悟新知
知识点
棱柱及其相关概念
3
1.棱柱 如图 25.2-6,这样的几何体叫做棱柱 .
(1) 底面: 它的上、下两个面叫做底面 .
(2) 侧面: 除底面外的其余各面叫做侧面 .
(3) 侧棱: 相邻侧面的交线叫做侧棱 .
两底面互相平行且全等.
所有侧棱平行且相等.
感悟新知
2. 直棱柱 当侧棱垂直于底面时,棱柱称为直棱柱 .
3. 正棱柱 底面是正多边形的直棱柱叫做正棱柱 .
感悟新知
知识储备
1.根据棱柱底面多边形的边数,依次称棱柱为三棱柱、四棱柱、五棱柱……
2.直棱柱的各个侧面都是矩形 .
3.直棱柱的展开图由所有的侧面和两个底面组成,侧面展开后可得到一个矩形,其长、宽分别是底面图形的周长和直棱柱的高 .
感悟新知
画出如图 25.2-7 所示的正三棱柱的三视图 .
例3
感悟新知
解: 三视图如图 25.2-8 所示 .
解题秘方:紧扣正三棱柱的特征及三视图的概念正确地画出三视图,关键要画准长、宽、高 .
感悟新知
画出图 25.2-9 中几何体的三视图 .
例4
感悟新知
解题秘方:紧扣“三视图的画法”画出几何体的三视图 .
解:该几何体由一个长方体和一个三棱柱组合而成,依据三视图的画法,可得该几何体的三视图如图 25.2-10 所示 .
感悟新知
画法提醒: 画几何体的三视图时,要仔细观察几何体,从要看的方向将几何体压缩到平面上,使几何体在这一方向上没有厚度,同时要特别注意三视图之间应遵循:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等 .
感悟新知
解题通法
画几何体的三视图的策略:
1.画几何体的三视图时, 一定要将几何体的边缘、棱、顶点都体现出来,看得见的轮廓线画成实线,看不见的轮廓线画成虚线,不能漏掉 .
2.画组合体的三视图时, 常利用图形分解的方法,将组合体分解成若干个简单几何体,画出这些简单几何体的三视图,然后按照原组合体将各种视图组合在一起 .
感悟新知
图解
依据“ 长 对 正、 高 平齐、宽相等”画出三视图如图 25.2-11 所示 .
感悟新知
知识点
由三视图确定几何体
4
1. 由三视图描述几何体形状的方法 由三视图想象几何体的形状,首先分别根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状,然后综合起来考虑整体形状 .
特别提醒: 由三视图描述几何体的形状时,要对三视图进行综合分析,一个方向的视图只能反映几何体的部分信息 .
感悟新知
2. 由三视图想象几何体形状的常用途径
(1)根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状以及几何体的“长、宽、高 ”;
(2)根据实线和虚线想象几何体看得见和看不见的轮廓线 ;
感悟新知
(3)熟记一些简单几何体的三视图会对复杂几何体的想象有帮助 ;
(4)利用由三视图画几何体与由几何体画三视图的互逆过程,反复练习,不断总结方法 .
感悟新知
要点解读
几何体、三视图和展开图之间的关系:
1. 几何体的三视图和展开图都是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形,即三者之间可以互相转化 .
2. 对于稍复杂的视图,可先将其分解成几个简单的图形,再综合分析 .
感悟新知
3. 一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,有多种可能性,如正方体的主视图是正方形,但主视图是正方形的几何体可能是直棱柱、长方体、圆柱等 .
感悟新知
3. 常见几何体的三视图
感悟新知
[ 中考·湖北 ] 如图 25.2-12 是一个立体图形的三视图,该立体图形是( )
A. 长方体 B. 正方体
C. 三棱柱 D. 圆柱
例5
感悟新知
答案:A
解题秘方:根据三视图直接判断即可.
解:根据三视图可知,该立体图形是长方体 .
感悟新知
方法点拨
本题主要考查立体图形的三视图,熟练掌握基本图形的三视图是解题的关键.
三视图
主视图
俯视图
左视图
三视图
画法
应用
请完成教材课后作业
作业提升
25.2 三视图
第二十五章 投影与视图
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
三视图及其相关概念
画几何体的三视图
棱柱及其相关概念
由三视图确定几何体
感悟新知
知识点
三视图及其相关概念
1
1.正面、水平面、侧面 用三个互相垂直的平面作为投影面,其中正对着我们的面叫做正面,下方的面叫做水平面,右边的面叫做侧面 .
感悟新知
三视图 对一个几何体在三个投影面内进行正投影,得到的三个平面图形组成这个几何体的三视图,其中:
(1) 主视图: 自几何体的前方向后投射,在正面投影面上得到的视图称为主视图;
(2)俯视图:自几何体的上方向下投射,在水平投影面上得到的视图称为俯视图;
(3)左视图:自几何体的左侧向右投射,在侧面投影面上得到的视图称为左视图 .
感悟新知
3. 三视图与正投影的关系 某些物体的三视图实际上是该物体在一定条件下所形成的正投影,某些物体的主视图、左视图、俯视图可以看成一束平行光线分别从物体的正面、左面、上面照射,在垂直于这些光线的平面上所形成的正投影 .
感悟新知
速记口诀
视图来源正投影,三个方向实物成,
从前向后主视图,从上向下俯视图,
从左向右左视图,统称物体三视图 .
感悟新知
示图
长方体的三视图如图 25.2-1:
感悟新知
[ 中考·梧州 ] 在如图 25.2-2 所示的立体图形中,主视图为矩形的是( )
例1
感悟新知
解:A. 圆柱的主视图是矩形,故本选项符合题意;
B. 球的主视图是圆,故本选项不符合题意;
C. 圆锥的主视图是等腰三角形,故本选项不符合题意;
D. 三棱锥的主视图是三角形,故本选项不符合题意.
解题秘方:根据主视图是从几何体正面看所得到的图形,分别得出四个几何体的主视图,即可解答.
答案:A
感悟新知
方法点拨
本题考查了简单几何体的主视图,注意主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
感悟新知
知识点
画几何体的三视图
2
1. 三视图之间的关系
(1)位置关系: 主视图在左上方,主视图的正下方是俯视图,主视图的正右方是左视图 . 主视图反映几何体的长与高,俯视图反映几何体的长与宽,左视图反映几何体的高与宽 .
感悟新知
(2) 大小关系:三视图之间的大小是相互联系的 . 主视图的长与俯视图的长对正,主视图的高与左视图的高平齐,俯视图的宽与左视图的宽相等 .
感悟新知
速记口诀
视图位置要摆明,画图规则要记清.
主俯视图长对正,左俯视图宽相等.
主左视图高平齐,实线虚线应分清 .
感悟新知
2. 三视图的画法:
(1)确定主视图的位置, 画出主视图;
(2)在主视图的正下方画出俯视图,并且主视图与俯视图的长对正;
感悟新知
(3)在主视图的正右方画出左视图,与主视图的高平齐,与俯视图的宽相等(可简述为长对正,高平齐,宽相等) . 图 25.2-3 ①中的几何体的三视图如图 25.2-3 ②所示 .
感悟新知
3. 画三视图的规定 画三视图时,看得见的部分的轮廓线画成实线,因被其他部分遮挡而看不见的部分的轮廓线画成虚线 .
感悟新知
一种机器上有一个零件叫燕尾槽(如图 25.2-4),请画出它的三视图 .
例2
感悟新知
解:这个燕尾槽的三视图如图 25.2-5 所示 .
感悟新知
知识点
棱柱及其相关概念
3
1.棱柱 如图 25.2-6,这样的几何体叫做棱柱 .
(1) 底面: 它的上、下两个面叫做底面 .
(2) 侧面: 除底面外的其余各面叫做侧面 .
(3) 侧棱: 相邻侧面的交线叫做侧棱 .
两底面互相平行且全等.
所有侧棱平行且相等.
感悟新知
2. 直棱柱 当侧棱垂直于底面时,棱柱称为直棱柱 .
3. 正棱柱 底面是正多边形的直棱柱叫做正棱柱 .
感悟新知
知识储备
1.根据棱柱底面多边形的边数,依次称棱柱为三棱柱、四棱柱、五棱柱……
2.直棱柱的各个侧面都是矩形 .
3.直棱柱的展开图由所有的侧面和两个底面组成,侧面展开后可得到一个矩形,其长、宽分别是底面图形的周长和直棱柱的高 .
感悟新知
画出如图 25.2-7 所示的正三棱柱的三视图 .
例3
感悟新知
解: 三视图如图 25.2-8 所示 .
解题秘方:紧扣正三棱柱的特征及三视图的概念正确地画出三视图,关键要画准长、宽、高 .
感悟新知
画出图 25.2-9 中几何体的三视图 .
例4
感悟新知
解题秘方:紧扣“三视图的画法”画出几何体的三视图 .
解:该几何体由一个长方体和一个三棱柱组合而成,依据三视图的画法,可得该几何体的三视图如图 25.2-10 所示 .
感悟新知
画法提醒: 画几何体的三视图时,要仔细观察几何体,从要看的方向将几何体压缩到平面上,使几何体在这一方向上没有厚度,同时要特别注意三视图之间应遵循:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等 .
感悟新知
解题通法
画几何体的三视图的策略:
1.画几何体的三视图时, 一定要将几何体的边缘、棱、顶点都体现出来,看得见的轮廓线画成实线,看不见的轮廓线画成虚线,不能漏掉 .
2.画组合体的三视图时, 常利用图形分解的方法,将组合体分解成若干个简单几何体,画出这些简单几何体的三视图,然后按照原组合体将各种视图组合在一起 .
感悟新知
图解
依据“ 长 对 正、 高 平齐、宽相等”画出三视图如图 25.2-11 所示 .
感悟新知
知识点
由三视图确定几何体
4
1. 由三视图描述几何体形状的方法 由三视图想象几何体的形状,首先分别根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状,然后综合起来考虑整体形状 .
特别提醒: 由三视图描述几何体的形状时,要对三视图进行综合分析,一个方向的视图只能反映几何体的部分信息 .
感悟新知
2. 由三视图想象几何体形状的常用途径
(1)根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状以及几何体的“长、宽、高 ”;
(2)根据实线和虚线想象几何体看得见和看不见的轮廓线 ;
感悟新知
(3)熟记一些简单几何体的三视图会对复杂几何体的想象有帮助 ;
(4)利用由三视图画几何体与由几何体画三视图的互逆过程,反复练习,不断总结方法 .
感悟新知
要点解读
几何体、三视图和展开图之间的关系:
1. 几何体的三视图和展开图都是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形,即三者之间可以互相转化 .
2. 对于稍复杂的视图,可先将其分解成几个简单的图形,再综合分析 .
感悟新知
3. 一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,有多种可能性,如正方体的主视图是正方形,但主视图是正方形的几何体可能是直棱柱、长方体、圆柱等 .
感悟新知
3. 常见几何体的三视图
感悟新知
[ 中考·湖北 ] 如图 25.2-12 是一个立体图形的三视图,该立体图形是( )
A. 长方体 B. 正方体
C. 三棱柱 D. 圆柱
例5
感悟新知
答案:A
解题秘方:根据三视图直接判断即可.
解:根据三视图可知,该立体图形是长方体 .
感悟新知
方法点拨
本题主要考查立体图形的三视图,熟练掌握基本图形的三视图是解题的关键.
三视图
主视图
俯视图
左视图
三视图
画法
应用
请完成教材课后作业
作业提升
