青岛版八下第6章平行四边形测试题

青岛版八下第6章平行四边形测试题
一、选择题(每小题3分，共36分)
1.平行四边形的一条对角线长为10，则它的一组邻边可能是（ ）
A. 4和6 B. 2和12 C. 4和8 D. 4和3 3题图
2．在平行四边形ABCD中，EF过对角线的交点O，若AB=4，BC=7，OE=3，则四边形EFCD周长是（ ）
A．14 B. 11 C. 10 D. 17
3．如图所示，在ABCD中，E、F分别AB、CD的中点，连结DE、EF、BF，则图中平行四边形共有（ ）
A．2个　　 B．4个　　 C．6个　　 D．8个
4． 一矩形两对角线之间的夹角有一个是600, 且这角所对的边长5cm,则对角线长为( )
A. 5 cm B. B. 10cm C. 5cm D. 无法确定
5．顺次连结对角线相等四边形各边上的中点，得到的新四边形是 ( )
A．矩形 B.正方形 C.菱形 D.平行四边形
6．已知菱形的周长为40cm，两条对角线的长度比为3：4，那么两条对角线的长分别为（ ）
A．6cm，8cm B. 3cm，4cm C. 12cm，16cm D. 24cm，32cm
7．下列各组图形中，对角线互相平分且垂直的是（ ）
A. 平行四边形与菱形 B. 矩形与正方形 C. 菱形与矩形 D. 菱形与正方形
8．如图在矩形ABCD中，对角线AC、BD相交于点O，则以下说法错误的是( )
A．AB=AD B．AC=BD C ．AO=OC=BO=∠OD
D．∠DAB=∠ABC=∠BCD=∠CDA=90°
9．如图a，一张正方形的纸张沿虚线对折一次得图b，再沿虚线对折一次得图c，
然后沿图c得的虚线（虚线与底边平行）剪去一个角，再打开后的形状是（ ） 8题图
A. B. C. D.
10．.如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：
甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．
乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．
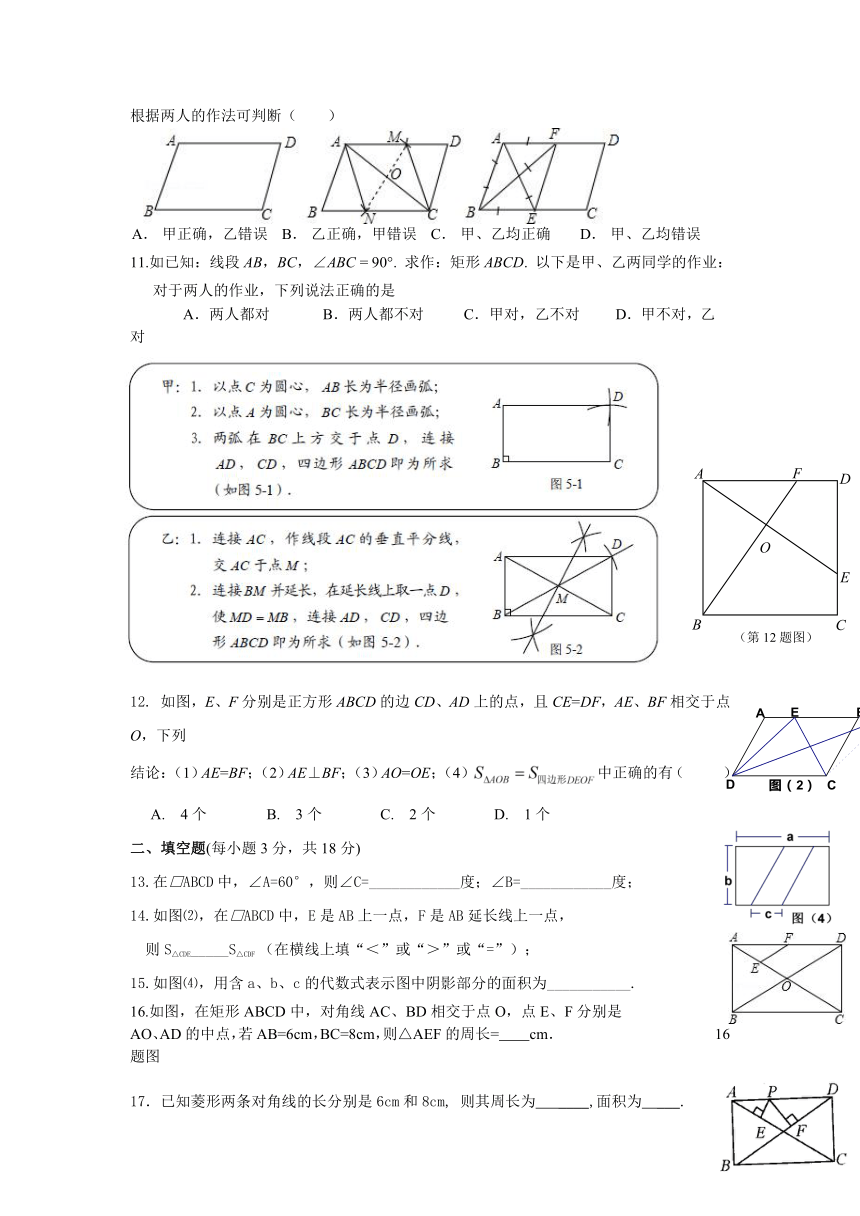
根据两人的作法可判断（　　）
　 A． 甲正确，乙错误 B． 乙正确，甲错误 C． 甲、乙均正确 D． 甲、乙均错误
11.如已知：线段AB，BC，∠ABC = 90°. 求作：矩形ABCD. 以下是甲、乙两同学的作业：
对于两人的作业，下列说法正确的是
A．两人都对 B．两人都不对 C．甲对，乙不对 D．甲不对，乙对
12. 如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列
结论：（1）AE=BF；（2）AE⊥BF；（3）AO=OE；（4）中正确的有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题(每小题3分，共18分)
13.在□ABCD中，∠A=60°，则∠C=____________度；∠B=____________度；
14.如图⑵，在□ABCD中，E是AB上一点，F是AB延长线上一点，
则S△CDE_____S△CDF （在横线上填“＜”或“＞”或“=”）；
15.如图⑷，用含a、b、c的代数式表示图中阴影部分的面积为___________.
16.如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是
AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长=　　cm． 16题图
17．已知菱形两条对角线的长分别是6cm和8cm, 则其周长为 ____,面积为 ___.
18．如图，矩形ABCD中，AB＝3，BC＝4，P是边AD上的动点，PE⊥AC于点E，
PF⊥BD于点F，则PE＋PF的值为：_________。
三、解答题 （共66分） 18题图
19．（本题8分）已知四边形ABCD，仅从下列条件中任取两个加以组合，能否得到四边形ABCD是平行四边形的结论？试一试，并说明理由（至少写3组）。
①AB=CD ②AB∥CD ③BC∥AD ④BC=AD ⑤∠A=∠C ⑥∠B=∠D
20．（本题8分）在一次数学探究活动中，小强用两条直线把平行四边形ABCD分割成四部分，使含有一组对角的两个图形相等。
⑴根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有几组；
⑵请在下图的三个平行四边形中画出满足小强分割方法的直线；
⑶由上述实验操作过程，你发现所画的两条直线有什么规律？
21. （本题8分）如图，四边形ABCD中，∠A=∠BCD=90°，BC=CD，CE⊥AD，垂足为E。
求证：AE=CE．
22．（本题10分）已知，在△ABC中，AB＝AC＝a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q。
⑴求四边形AQMP的周长；
⑵M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由。
23. （本题10分）如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．
（1）求证：四边形AEBD是矩形；
（2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．
24.（本题10分）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F,连接CF.
（1）求证：AF=DC；
（2）若AB⊥AC,试判断四边形ADCF的形状，并证明你的结论.
25．（本题12分） 如图，正方形ABCD中，E是对角线BD上一点，
过E点作矩形EFCG，其中点F在BC上，点G在DC上。
⑴试说明EG=DG，EF=BF
⑵若正方形的面积为25cm2，求矩形EFCG的周长。
(3)连结AE、FG.求证AE=FG.
参考答案：（特别说明：有个别试题用的勾股定理）
一、1-6 B D B B B C 7-12 D A D C A B
二、13.60,120 14.= 15. b（a-c）或ab-bc 16. 9 17.40cm, 24c㎡ 18. 1.2
三、19、答案不唯一如：（1）（2）；（2）（3）；（2）（5）；（2）(6)；(3)(4)；（5）（6）等
20. ⑴无数多组 (2) 略 ⑶两条直线的交点即为两对角线的交点
21、证明：如图，过点B作BF⊥CE于F，
∵CE⊥AD，∴∠D+∠DCE=90°，
∵∠BCD=90°，∴∠BCF+∠DCE=90°，
∴∠BCF=∠D，在△BCF和△CDE中，，
∴△BCF≌△CDE（AAS），
∴BF=CE，
又∵∠A=90°，CE⊥AD，BF⊥CE， ∴四边形AEFB是矩形，
∴AE=BF，
∴AE=CE．
22、（1）2a (2) M位于BC的中点位置时，四边形AQMP为菱形BC的
23、（1）证明：∵点O为AB的中点，连接DO并延长到点E，使OE=OD，
∴四边形AEBD是平行四边形，
∵AB=AC，AD是△ABC的角平分线，∴AD⊥BC，∴∠ADB=90°，
∴平行四边形AEBD是矩形；
（2）当∠BAC=90°时，
理由：∵∠BAC=90°，AB=AC，AD是△ABC的角平分线，
∴AD=BD=CD，
∵由（1）得四边形AEBD是矩形，
∴矩形AEBD是正方形．
24、证明：（1）∵E是AD的中点，∴AE=ED.
∵AF∥BC,∴∠AFE=∠DBE, ∠FAE=∠BDE, ∴△AFE≌△DBE.
∴AF=DB.
∵AD是BC边上的中点，
∴DB=DC,AF=DC
（2）四边形ADCF是菱形.
理由：由（1）知，AF=DC,
∵AF∥CD, ∴四边形ADCF是平行四边形.
又∵AB⊥AC, ∴△ABC是直角三角形
∵AD是BC边上的中线,
∴.
∴平行四边形ADCF是菱形.
25. ⑴提示：证∠DBF=∠BEF=∠DEG=∠BDG=45° ⑵10cm或14.14cm
（3）提示：连接EC,证明EC=AE, EC=FG
F
（第12题图）
A
B
C
D
O
E