2023年中考数学专题复习讲义——定角问题(花生模型)(无答案)
文档属性
| 名称 | 2023年中考数学专题复习讲义——定角问题(花生模型)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 08:20:06 | ||
图片预览

文档简介
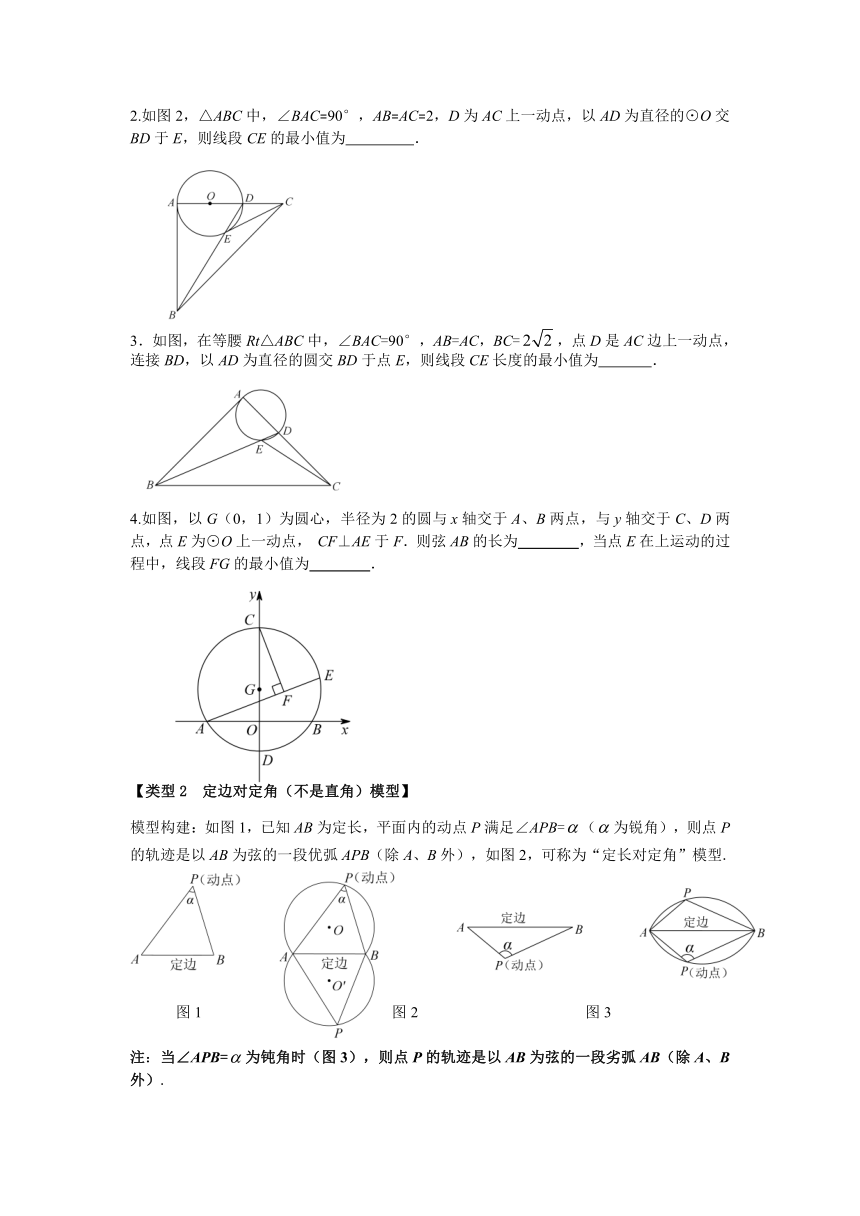
中考专题复习——定角问题(花生模型)
模型建构 :
当∠P保持不变,∠P所对的边AB长为定值,则∠P 的顶点P 的轨迹为两条圆弧(除A、B两点).
简称:定边对定角(花生模型)
【类型1 定边对直角模型】
动态问题中一般会出现多个直角,往往会有一个直角所对斜边是固定不变的,选取该斜边中点为圆心,斜边中线为半径.
模型构建:如图1,已知AB为定长,平面内的动点P满足∠APB=90°,则点P的轨迹是以AB为直径的圆(除A、B外),如图2,可称为“定长对直角”模型.
图1 图2
例1. 在正方形ABCD 中,AD=2,E,F 分别为边DC,CB 上的点,且始终保持DE=CF,连接AE 和DF 交于点P,则线段CP 的最小值为___________.
举一反三
1.如图1,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠APB=90°,则线段CP长的最小值为 .
2.如图2,△ABC中,∠BAC=90°,AB=AC=2,D为AC上一动点,以AD为直径的⊙O交BD于E,则线段CE的最小值为 .
3.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .
4.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙O上一动点, CF⊥AE于F.则弦AB的长为 ,当点E在上运动的过程中,线段FG的最小值为 .
【类型2 定边对定角(不是直角)模型】
模型构建:如图1,已知AB为定长,平面内的动点P满足∠APB=(为锐角),则点P的轨迹是以AB为弦的一段优弧APB(除A、B外),如图2,可称为“定长对定角”模型.
图1 图2 图3
注:当∠APB=为钝角时(图3),则点P的轨迹是以AB为弦的一段劣弧AB(除A、B外).
例题1:如图1,在△ABC中,BC=4,∠BAC=60°,请你利用直尺和圆规在平面内找一点P,
使得点P到边AB、BC的距离相等,且∠BPC=60°.
例题2.(1)如图1,点A、B、C分别是⊙O上不重合的三点,连接AC、BC. 点P是直线AB上方且在⊙O外的任意一点, 连接AP、BP.试比较∠APB与∠ACB的大小关系,并说明理由;
(2)如图2,若点Q是⊙O内任意一点, 连接AQ、BQ,则∠AQB ∠ACB;
(3)如图3,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).
①若在第一象限内有一点P,且满足∠APB=45°,请你利用直尺和圆规在y轴正半轴上找一点Q,使得∠AQB=45°,试问:这样的点Q有几个?你能求出点Q的坐标吗?
图1 图2
图3
②若点C是y轴正半轴上一个动点,试问∠ACB是否有最大值?
如果有,请求出点C的坐标;如果没有请说明理由.
举一反三
1.在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(,0)、B(3,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A.2﹣2 B.2
C.2 D.2
追问1 线段CD的长的最大值是 .
追问2 如果将2中的∠ADB改为30°,线段CD的长的最小值是 .
2.在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(,0)、B(3,0)、C(0,5),点D在第一象限内,且∠ADB=45°,则线段CD的长的最小值是___________.
3.如图,已知△ABC,在BC的左侧找一点E,使得∠BEC=∠BAC,CE=BE.
4.如图,在 □ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
(1)求证:∠BFC=∠D.
(2)在直线AD找一点P,使得∠BPC=∠D.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)
类型4 对角互补时,有辅助圆
如图, 若∠P+∠1=180°,则A、P、B、Q
四点在同一个圆上
如图,在平面直角坐标系xOy中,点A(-3,0);B(1,1),C(0,3).过点B作BD⊥x轴,垂足为点D,连接CD.
(1)若点M是y轴上一点,当AM⊥CD时,点M 的坐标为______;
(2)若点P是△ABC的外心,求点P的坐标;
(3)在x轴上是否存在点Q,使得∠BQD=∠ACB,若存在,直接写出点Q的坐标;若不存在,说明理由.
举一反三
1.如图,已知平面直角坐标系中,直线y=kx(k≠0)经过点(a,a)(a>0).线段BC的两个端点分别在x轴与直线y=kx上(B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P,经探究在整个滑动过程中,P、O两点间的距离为定值_____________.
模型建构 :
当∠P保持不变,∠P所对的边AB长为定值,则∠P 的顶点P 的轨迹为两条圆弧(除A、B两点).
简称:定边对定角(花生模型)
【类型1 定边对直角模型】
动态问题中一般会出现多个直角,往往会有一个直角所对斜边是固定不变的,选取该斜边中点为圆心,斜边中线为半径.
模型构建:如图1,已知AB为定长,平面内的动点P满足∠APB=90°,则点P的轨迹是以AB为直径的圆(除A、B外),如图2,可称为“定长对直角”模型.
图1 图2
例1. 在正方形ABCD 中,AD=2,E,F 分别为边DC,CB 上的点,且始终保持DE=CF,连接AE 和DF 交于点P,则线段CP 的最小值为___________.
举一反三
1.如图1,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠APB=90°,则线段CP长的最小值为 .
2.如图2,△ABC中,∠BAC=90°,AB=AC=2,D为AC上一动点,以AD为直径的⊙O交BD于E,则线段CE的最小值为 .
3.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .
4.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙O上一动点, CF⊥AE于F.则弦AB的长为 ,当点E在上运动的过程中,线段FG的最小值为 .
【类型2 定边对定角(不是直角)模型】
模型构建:如图1,已知AB为定长,平面内的动点P满足∠APB=(为锐角),则点P的轨迹是以AB为弦的一段优弧APB(除A、B外),如图2,可称为“定长对定角”模型.
图1 图2 图3
注:当∠APB=为钝角时(图3),则点P的轨迹是以AB为弦的一段劣弧AB(除A、B外).
例题1:如图1,在△ABC中,BC=4,∠BAC=60°,请你利用直尺和圆规在平面内找一点P,
使得点P到边AB、BC的距离相等,且∠BPC=60°.
例题2.(1)如图1,点A、B、C分别是⊙O上不重合的三点,连接AC、BC. 点P是直线AB上方且在⊙O外的任意一点, 连接AP、BP.试比较∠APB与∠ACB的大小关系,并说明理由;
(2)如图2,若点Q是⊙O内任意一点, 连接AQ、BQ,则∠AQB ∠ACB;
(3)如图3,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).
①若在第一象限内有一点P,且满足∠APB=45°,请你利用直尺和圆规在y轴正半轴上找一点Q,使得∠AQB=45°,试问:这样的点Q有几个?你能求出点Q的坐标吗?
图1 图2
图3
②若点C是y轴正半轴上一个动点,试问∠ACB是否有最大值?
如果有,请求出点C的坐标;如果没有请说明理由.
举一反三
1.在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(,0)、B(3,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A.2﹣2 B.2
C.2 D.2
追问1 线段CD的长的最大值是 .
追问2 如果将2中的∠ADB改为30°,线段CD的长的最小值是 .
2.在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(,0)、B(3,0)、C(0,5),点D在第一象限内,且∠ADB=45°,则线段CD的长的最小值是___________.
3.如图,已知△ABC,在BC的左侧找一点E,使得∠BEC=∠BAC,CE=BE.
4.如图,在 □ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
(1)求证:∠BFC=∠D.
(2)在直线AD找一点P,使得∠BPC=∠D.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)
类型4 对角互补时,有辅助圆
如图, 若∠P+∠1=180°,则A、P、B、Q
四点在同一个圆上
如图,在平面直角坐标系xOy中,点A(-3,0);B(1,1),C(0,3).过点B作BD⊥x轴,垂足为点D,连接CD.
(1)若点M是y轴上一点,当AM⊥CD时,点M 的坐标为______;
(2)若点P是△ABC的外心,求点P的坐标;
(3)在x轴上是否存在点Q,使得∠BQD=∠ACB,若存在,直接写出点Q的坐标;若不存在,说明理由.
举一反三
1.如图,已知平面直角坐标系中,直线y=kx(k≠0)经过点(a,a)(a>0).线段BC的两个端点分别在x轴与直线y=kx上(B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P,经探究在整个滑动过程中,P、O两点间的距离为定值_____________.
同课章节目录
