2023年中考数学专题复习讲义——二次函数背景下的倍角、半角与等角(无答案)
文档属性
| 名称 | 2023年中考数学专题复习讲义——二次函数背景下的倍角、半角与等角(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 08:20:59 | ||
图片预览

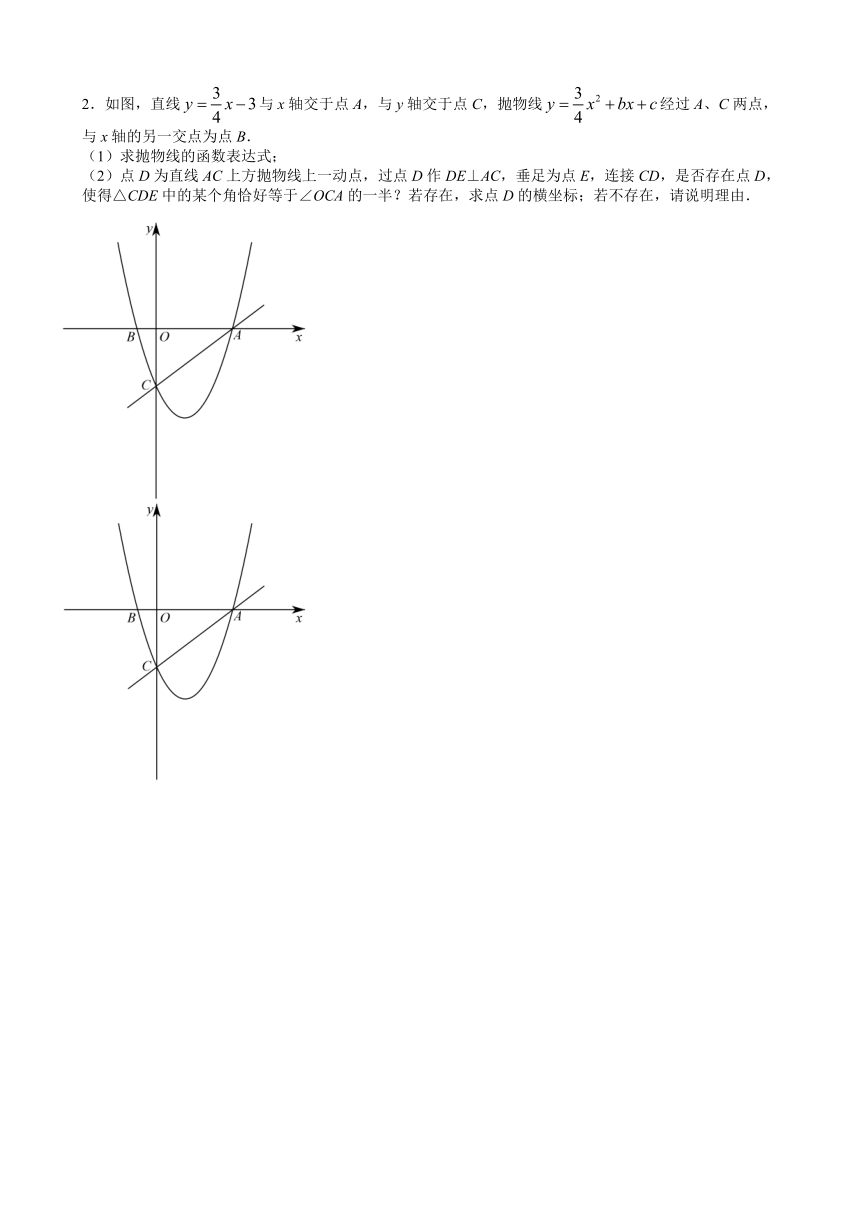
文档简介
中考专题复习——二次函数背景下的倍角、半角与等角
在坐标系中构造已知角的半角或二倍角,角可以单独出现,也可以存在于某个几何图形中,因此,构造半角、二倍角的方法也并不唯一,常用如下∶
一.解题策略回顾:已知一个角的三角函数值怎样求它的倍半角的三角函数值
(1) 如图,在△ABC中,∠C=90°,若∠B的三角函数值已知,怎样求∠B一半角的三角函数值?
通常的方法:延长CB到点D,使得BD=BA,则可得∠D=∠ABC.
(2) 如图,在△ABC中,∠C=90°,BC>AC,若∠B的三角函数值已知,怎样求∠B两倍角的三角函数值?
通常的方法:作斜边AB的垂直平分线DE,交BC于点D,交AB于点E,则可得∠ADC=2∠ABC.
二、例题讲解:
1.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,抛物线经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点,过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.
2.如图,直线与x轴交于点A,与y轴交于点C,抛物线经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点,过点D作DE⊥AC,垂足为点E,连接CD,是否存在点D,使得△CDE中的某个角恰好等于∠OCA的一半?若存在,求点D的横坐标;若不存在,请说明理由.
3.如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
当堂训练:
1.如图,抛物线交x轴于A、B两点,交y轴于点C,直线经过点B、C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B、C重合),作直线AM的平行线交直线BC于点Q,若以点A、M、P、Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
2.如图,抛物线 y= x +bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y 轴交于点C(0,-3).
(1)求抛物线的函数表达式;
(2)如图,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
3.如图,在平面直角坐标系中,直线 与x 轴交于点A,与y 轴交于点 B,抛物线 经过 A、B 两点且与x 轴的负半轴交于点 C.
(1)求该抛物线的解析式;
(2)若点D为直线AB 上方抛物线上的一个动点,当∠ABD=2∠BAC时,求点D的坐标.
4.如图1,四边形OABC 是矩形,点A的坐标为(3,0),点 C的坐标为(0,6),点 P 从点 0出发,沿 OA 以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿 AB 以每秒 2 个单位长度的速度向点 B 运动,当点P与点A重合时运动停止.设运动时间为 t秒.
问题∶当 t=1时,抛物线 y=x"+bx+c 经过P、Q两点,与y 轴交于点M,抛物线的顶点为 K,如图所示,问该抛物线上是否存在点 D,使∠MQD= ∠MKQ 若存在,求出所有满足条件的 D的坐标;若不存在,说明理由.
在坐标系中构造已知角的半角或二倍角,角可以单独出现,也可以存在于某个几何图形中,因此,构造半角、二倍角的方法也并不唯一,常用如下∶
一.解题策略回顾:已知一个角的三角函数值怎样求它的倍半角的三角函数值
(1) 如图,在△ABC中,∠C=90°,若∠B的三角函数值已知,怎样求∠B一半角的三角函数值?
通常的方法:延长CB到点D,使得BD=BA,则可得∠D=∠ABC.
(2) 如图,在△ABC中,∠C=90°,BC>AC,若∠B的三角函数值已知,怎样求∠B两倍角的三角函数值?
通常的方法:作斜边AB的垂直平分线DE,交BC于点D,交AB于点E,则可得∠ADC=2∠ABC.
二、例题讲解:
1.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,抛物线经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点,过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.
2.如图,直线与x轴交于点A,与y轴交于点C,抛物线经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点,过点D作DE⊥AC,垂足为点E,连接CD,是否存在点D,使得△CDE中的某个角恰好等于∠OCA的一半?若存在,求点D的横坐标;若不存在,请说明理由.
3.如图,已知:抛物线y=a(x+1)(x﹣3)与x轴相交于A、B两点,与y轴的交于点C(0,﹣3).
(1)求抛物线的解析式的一般式.
(2)若抛物线上有一点P,满足∠ACO=∠PCB,求P点坐标.
(3)直线l:y=kx﹣k+2与抛物线交于E、F两点,当点B到直线l的距离最大时,求△BEF的面积.
当堂训练:
1.如图,抛物线交x轴于A、B两点,交y轴于点C,直线经过点B、C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B、C重合),作直线AM的平行线交直线BC于点Q,若以点A、M、P、Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
2.如图,抛物线 y= x +bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y 轴交于点C(0,-3).
(1)求抛物线的函数表达式;
(2)如图,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
3.如图,在平面直角坐标系中,直线 与x 轴交于点A,与y 轴交于点 B,抛物线 经过 A、B 两点且与x 轴的负半轴交于点 C.
(1)求该抛物线的解析式;
(2)若点D为直线AB 上方抛物线上的一个动点,当∠ABD=2∠BAC时,求点D的坐标.
4.如图1,四边形OABC 是矩形,点A的坐标为(3,0),点 C的坐标为(0,6),点 P 从点 0出发,沿 OA 以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿 AB 以每秒 2 个单位长度的速度向点 B 运动,当点P与点A重合时运动停止.设运动时间为 t秒.
问题∶当 t=1时,抛物线 y=x"+bx+c 经过P、Q两点,与y 轴交于点M,抛物线的顶点为 K,如图所示,问该抛物线上是否存在点 D,使∠MQD= ∠MKQ 若存在,求出所有满足条件的 D的坐标;若不存在,说明理由.
同课章节目录
