北师大版七年级下册1.4.3多项式与多项式相乘 同步练习(含答案)
文档属性
| 名称 | 北师大版七年级下册1.4.3多项式与多项式相乘 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 56.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 11:23:48 | ||
图片预览


文档简介
1.4 整式的乘法
第3课时 多项式与多项式相乘
一、选择题
1.计算(2x-3)(3x+4)的结果是( )
A.-7x+4 B.-7x-12 C.6x2-12 D.6x2-x-12
2.【2022·遂宁】下列计算中正确的是( )
A.a3·a3=a9 B.(-2a)3=-8a3
C.a10÷(-a2)3=a4 D.(-a+2)(-a-2)=a2+4
3.下列各式的结果为m2-7m+12的是( )
A.(m-3)(m+4) B.(m-3)(m-4)
C.(m+3)(m-4) D.(m+3)(m+4)
4.若(x+2)·(x-1)=x2+mx+n,则m+n的值为( )
A.1 B.-2 C.-1 D.2
5.已知m+n=2,mn=-2,则(2-m)(2-n)的值为( )
A.2 B.-2 C.0 D.3
6.若多项式(x2+mx+n)(x2-3x+4)展开后不含x3和x2项,则m,n的值分别是( )
A.3,5 B.5,3 C.4,2 D.2,4
7.若(x+y+2)(x+y-1)=0,则x+y的值为( )
A.1 B.-2 C.2或-1 D.-2或1
8.若(x+4)(x-3)=x2+ax+b,则a,b的值是( )
A.a=-1,b=-12 B.a=1,b=-12
C.a=-1,b=12 D.a=1,b=12
9.如果一个长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
10.【2021·宜昌】从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
二、填空题
11.如果(2x-3)(5-2x)=ax2+bx+c,那么a= ,b= ,c= .
12.若(ax+3y)(x-y)的展开式不含xy项,则a的值为 .
13.已知:(x+1)(x+2)=ax2+bx+c,则4a-2b+c的值为 .
14.已知a(b-1)=b+1,则(a-1)(b-1)= .
三、解答题
15.先化简,再求值:(x+y+2)(x+y-2)-(x+2y)2+3y2 ,其中xy=-.
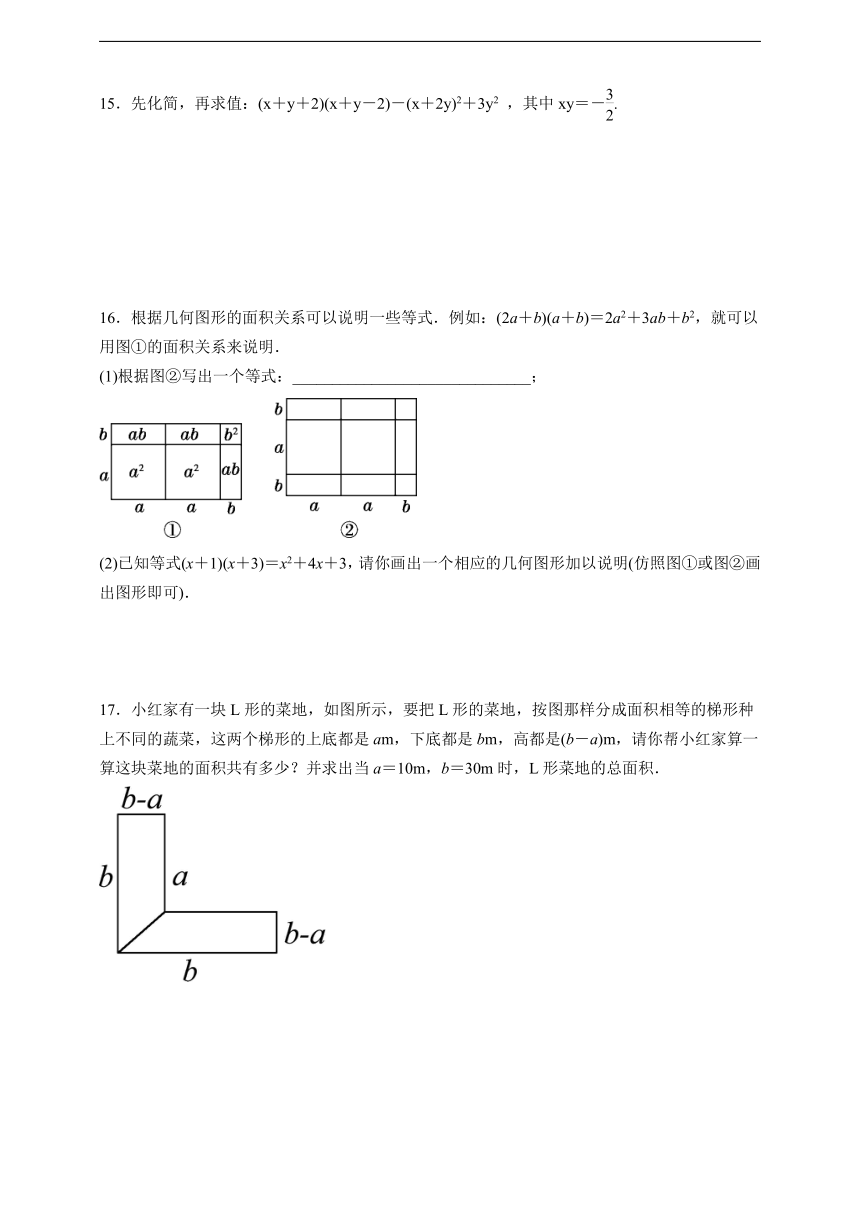
16.根据几何图形的面积关系可以说明一些等式.例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式:______________________________;
(2)已知等式(x+1)(x+3)=x2+4x+3,请你画出一个相应的几何图形加以说明(仿照图①或图②画出图形即可).
17.小红家有一块L形的菜地,如图所示,要把L形的菜地,按图那样分成面积相等的梯形种上不同的蔬菜,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你帮小红家算一算这块菜地的面积共有多少?并求出当a=10m,b=30m时,L形菜地的总面积.
18.甲、乙两人共同计算一道整式乘法:(2x+a)·(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10,由于乙漏抄了第二个多项式中x的系数,得到的结果为2x2-9x+10.
(1)你能知道式子中a、b的值各是多少?
(2)请你算出正确结果.
19.我们规定一种运算:=ad-bc,例如=3×6-4×5=-2,=4x+6.
按照这种运算规定,当x等于多少时,=0
参考答案
一、选择题
1.计算(2x-3)(3x+4)的结果是( D )
A.-7x+4 B.-7x-12 C.6x2-12 D.6x2-x-12
2.【2022·遂宁】下列计算中正确的是( B )
A.a3·a3=a9 B.(-2a)3=-8a3
C.a10÷(-a2)3=a4 D.(-a+2)(-a-2)=a2+4
3.下列各式的结果为m2-7m+12的是( B )
A.(m-3)(m+4) B.(m-3)(m-4)
C.(m+3)(m-4) D.(m+3)(m+4)
4.若(x+2)·(x-1)=x2+mx+n,则m+n的值为( C )
A.1 B.-2 C.-1 D.2
5.已知m+n=2,mn=-2,则(2-m)(2-n)的值为( B )
A.2 B.-2 C.0 D.3
【解析】(2-m)(2-n)=4-2(m+n)+mn.
因为m+n=2,mn=-2,
所以原式=4-4-2=-2.
6.若多项式(x2+mx+n)(x2-3x+4)展开后不含x3和x2项,则m,n的值分别是( A )
A.3,5 B.5,3 C.4,2 D.2,4
【解析】原式=x4+(m-3)x3+(n-3m+4)x2+(4m-3n)x+4n. 由题意得m-3=0,n-3m+4=0,所以m=3,n=5.
7.若(x+y+2)(x+y-1)=0,则x+y的值为( D )
A.1 B.-2 C.2或-1 D.-2或1
【解析】因为(x+y+2)(x+y-1)=0,
所以x+y+2=0或x+y-1=0,
解得x+y=-2或x+y=1.
8.若(x+4)(x-3)=x2+ax+b,则a,b的值是( B )
A.a=-1,b=-12 B.a=1,b=-12
C.a=-1,b=12 D.a=1,b=12
9.如果一个长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( D )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
10.【2021·宜昌】从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( C )
A.没有变化 B.变大了 C.变小了 D.无法确定
二、填空题
11.如果(2x-3)(5-2x)=ax2+bx+c,那么a= ,b= ,c= .
【答案】-4 16 -15
12.若(ax+3y)(x-y)的展开式不含xy项,则a的值为 .
【答案】3
13.已知:(x+1)(x+2)=ax2+bx+c,则4a-2b+c的值为 .
【答案】0
14.已知a(b-1)=b+1,则(a-1)(b-1)= .
【答案】2
三、解答题
15.先化简,再求值:(x+y+2)(x+y-2)-(x+2y)2+3y2 ,其中xy=-.
解:原式=x2+xy-2x+xy+y2-2y+2x+
2y-4-x2-2xy-2xy-4y2+3y2
=-2xy-4.
因为xy=-.
所以原式=-2×-4=-1.
16.根据几何图形的面积关系可以说明一些等式.例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式:______________________________;
【答案】(2a+b)(a+2b)=2a2+5ab+2b2
【总结】仿照例子可以看出,根据整个图形的面积等于各部分面积的和列式;
(2)已知等式(x+1)(x+3)=x2+4x+3,请你画出一个相应的几何图形加以说明(仿照图①或图②画出图形即可).
解:(x+1)(x+3)=x2+4x+3,相应的几何图形如图所示.
17.小红家有一块L形的菜地,如图所示,要把L形的菜地,按图那样分成面积相等的梯形种上不同的蔬菜,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你帮小红家算一算这块菜地的面积共有多少?并求出当a=10m,b=30m时,L形菜地的总面积.
解:由题意得这块菜地的面积为2×(a+b)(b-a)=(b2-a2)m2,当a=10m,b=30m时,原式=302-102=800(m2).
18.甲、乙两人共同计算一道整式乘法:(2x+a)·(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10,由于乙漏抄了第二个多项式中x的系数,得到的结果为2x2-9x+10.
(1)你能知道式子中a、b的值各是多少?
解:∵(2x-a)(3x+b)=6x2+(2b-3a)x-ab,∴,又∵(2x+a)(x+b)=2x2+(2b+a)x+ab,∴,由上得a=-5,b=-2;
(2)请你算出正确结果.
解:∵(2x-5)(3x-2)=6x2-19x+10,∴正确结果为:6x2-19x+10.
19.我们规定一种运算:=ad-bc,例如=3×6-4×5=-2,=4x+6.
按照这种运算规定,当x等于多少时,=0
解:因为=ad-bc,=0,
所以(x+1)(x-1)-(x-2)(x+3)=0,
x2-1-(x2+x-6)=0,
x2-1-x2-x+6=0,
-x=-5,即x=5.
故当x=5时,=0.
第3课时 多项式与多项式相乘
一、选择题
1.计算(2x-3)(3x+4)的结果是( )
A.-7x+4 B.-7x-12 C.6x2-12 D.6x2-x-12
2.【2022·遂宁】下列计算中正确的是( )
A.a3·a3=a9 B.(-2a)3=-8a3
C.a10÷(-a2)3=a4 D.(-a+2)(-a-2)=a2+4
3.下列各式的结果为m2-7m+12的是( )
A.(m-3)(m+4) B.(m-3)(m-4)
C.(m+3)(m-4) D.(m+3)(m+4)
4.若(x+2)·(x-1)=x2+mx+n,则m+n的值为( )
A.1 B.-2 C.-1 D.2
5.已知m+n=2,mn=-2,则(2-m)(2-n)的值为( )
A.2 B.-2 C.0 D.3
6.若多项式(x2+mx+n)(x2-3x+4)展开后不含x3和x2项,则m,n的值分别是( )
A.3,5 B.5,3 C.4,2 D.2,4
7.若(x+y+2)(x+y-1)=0,则x+y的值为( )
A.1 B.-2 C.2或-1 D.-2或1
8.若(x+4)(x-3)=x2+ax+b,则a,b的值是( )
A.a=-1,b=-12 B.a=1,b=-12
C.a=-1,b=12 D.a=1,b=12
9.如果一个长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
10.【2021·宜昌】从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
二、填空题
11.如果(2x-3)(5-2x)=ax2+bx+c,那么a= ,b= ,c= .
12.若(ax+3y)(x-y)的展开式不含xy项,则a的值为 .
13.已知:(x+1)(x+2)=ax2+bx+c,则4a-2b+c的值为 .
14.已知a(b-1)=b+1,则(a-1)(b-1)= .
三、解答题
15.先化简,再求值:(x+y+2)(x+y-2)-(x+2y)2+3y2 ,其中xy=-.
16.根据几何图形的面积关系可以说明一些等式.例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式:______________________________;
(2)已知等式(x+1)(x+3)=x2+4x+3,请你画出一个相应的几何图形加以说明(仿照图①或图②画出图形即可).
17.小红家有一块L形的菜地,如图所示,要把L形的菜地,按图那样分成面积相等的梯形种上不同的蔬菜,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你帮小红家算一算这块菜地的面积共有多少?并求出当a=10m,b=30m时,L形菜地的总面积.
18.甲、乙两人共同计算一道整式乘法:(2x+a)·(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10,由于乙漏抄了第二个多项式中x的系数,得到的结果为2x2-9x+10.
(1)你能知道式子中a、b的值各是多少?
(2)请你算出正确结果.
19.我们规定一种运算:=ad-bc,例如=3×6-4×5=-2,=4x+6.
按照这种运算规定,当x等于多少时,=0
参考答案
一、选择题
1.计算(2x-3)(3x+4)的结果是( D )
A.-7x+4 B.-7x-12 C.6x2-12 D.6x2-x-12
2.【2022·遂宁】下列计算中正确的是( B )
A.a3·a3=a9 B.(-2a)3=-8a3
C.a10÷(-a2)3=a4 D.(-a+2)(-a-2)=a2+4
3.下列各式的结果为m2-7m+12的是( B )
A.(m-3)(m+4) B.(m-3)(m-4)
C.(m+3)(m-4) D.(m+3)(m+4)
4.若(x+2)·(x-1)=x2+mx+n,则m+n的值为( C )
A.1 B.-2 C.-1 D.2
5.已知m+n=2,mn=-2,则(2-m)(2-n)的值为( B )
A.2 B.-2 C.0 D.3
【解析】(2-m)(2-n)=4-2(m+n)+mn.
因为m+n=2,mn=-2,
所以原式=4-4-2=-2.
6.若多项式(x2+mx+n)(x2-3x+4)展开后不含x3和x2项,则m,n的值分别是( A )
A.3,5 B.5,3 C.4,2 D.2,4
【解析】原式=x4+(m-3)x3+(n-3m+4)x2+(4m-3n)x+4n. 由题意得m-3=0,n-3m+4=0,所以m=3,n=5.
7.若(x+y+2)(x+y-1)=0,则x+y的值为( D )
A.1 B.-2 C.2或-1 D.-2或1
【解析】因为(x+y+2)(x+y-1)=0,
所以x+y+2=0或x+y-1=0,
解得x+y=-2或x+y=1.
8.若(x+4)(x-3)=x2+ax+b,则a,b的值是( B )
A.a=-1,b=-12 B.a=1,b=-12
C.a=-1,b=12 D.a=1,b=12
9.如果一个长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( D )
A.8a3-4a2+2a-1 B.8a3+4a2-2a-1
C.8a3-1 D.8a3+1
10.【2021·宜昌】从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( C )
A.没有变化 B.变大了 C.变小了 D.无法确定
二、填空题
11.如果(2x-3)(5-2x)=ax2+bx+c,那么a= ,b= ,c= .
【答案】-4 16 -15
12.若(ax+3y)(x-y)的展开式不含xy项,则a的值为 .
【答案】3
13.已知:(x+1)(x+2)=ax2+bx+c,则4a-2b+c的值为 .
【答案】0
14.已知a(b-1)=b+1,则(a-1)(b-1)= .
【答案】2
三、解答题
15.先化简,再求值:(x+y+2)(x+y-2)-(x+2y)2+3y2 ,其中xy=-.
解:原式=x2+xy-2x+xy+y2-2y+2x+
2y-4-x2-2xy-2xy-4y2+3y2
=-2xy-4.
因为xy=-.
所以原式=-2×-4=-1.
16.根据几何图形的面积关系可以说明一些等式.例如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式:______________________________;
【答案】(2a+b)(a+2b)=2a2+5ab+2b2
【总结】仿照例子可以看出,根据整个图形的面积等于各部分面积的和列式;
(2)已知等式(x+1)(x+3)=x2+4x+3,请你画出一个相应的几何图形加以说明(仿照图①或图②画出图形即可).
解:(x+1)(x+3)=x2+4x+3,相应的几何图形如图所示.
17.小红家有一块L形的菜地,如图所示,要把L形的菜地,按图那样分成面积相等的梯形种上不同的蔬菜,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你帮小红家算一算这块菜地的面积共有多少?并求出当a=10m,b=30m时,L形菜地的总面积.
解:由题意得这块菜地的面积为2×(a+b)(b-a)=(b2-a2)m2,当a=10m,b=30m时,原式=302-102=800(m2).
18.甲、乙两人共同计算一道整式乘法:(2x+a)·(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10,由于乙漏抄了第二个多项式中x的系数,得到的结果为2x2-9x+10.
(1)你能知道式子中a、b的值各是多少?
解:∵(2x-a)(3x+b)=6x2+(2b-3a)x-ab,∴,又∵(2x+a)(x+b)=2x2+(2b+a)x+ab,∴,由上得a=-5,b=-2;
(2)请你算出正确结果.
解:∵(2x-5)(3x-2)=6x2-19x+10,∴正确结果为:6x2-19x+10.
19.我们规定一种运算:=ad-bc,例如=3×6-4×5=-2,=4x+6.
按照这种运算规定,当x等于多少时,=0
解:因为=ad-bc,=0,
所以(x+1)(x-1)-(x-2)(x+3)=0,
x2-1-(x2+x-6)=0,
x2-1-x2-x+6=0,
-x=-5,即x=5.
故当x=5时,=0.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
