河北省邯郸市部分学校2023届高三下学期开学考试数学试题(含解析)
文档属性
| 名称 | 河北省邯郸市部分学校2023届高三下学期开学考试数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-02 00:00:00 | ||
图片预览




文档简介
邯郸市部分学校2023届高三下学期开学考试 数学
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本卷命题范围:高考范围.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,则( )
A. B. C. D.
2.已知空间四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面内”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若双曲线的两条渐近线互相垂直,则( )
A. B. C.2 D.
4.已知,则( )
A. B. C. D.
5.已知复数z的实部和虚部均为整数,则满足的复数z的个数为( )
A.2 B.3 C.4 D.5
6.函数在区间上的零点个数为( )
A.10 B.8 C.6 D.4
7.将函数的图象向右平移1个单位长度后,再向上平移4个单位长度,所得函数图象与曲线关于直线对称,则( )
A. B. C. D.4
8.已知O是的外心,且满足,若在上的投影向量为,则( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.若函数的最小正周期为,则( )
A. B.的图象与函数的图象重合
C. D.存在唯一的,使得
10.设A,B是两个随机事件,且,若B发生时A必定发生,则下列结论错误的是( )
A. B. C. D.
11.已知,若,则( )
A. B. C. D.
12.已知曲线C的方程为,点P在C上,O为坐标原点,则( )
A.曲线C关于原点对称
B.
C.设C与坐标轴所围成图形的面积为S,则
D.若M是直线上的一点,则
三、填空题:本题共4小题,每小题5分,共20分.
13.若直线与圆相交于A,B两点,当取得最小值时,直线l的斜率为____________.
14.2022年9月19日,航天科技集团五院发布消息称,近日在法国巴黎召开的第73届国际宇航大会上,我国火星探测天问一号任务团队首次获得国际宇航联合会2022年度世界航天奖.为科普航天知识,某校组织学生参与航天知识竞答活动,某班8位同学的得分成绩如下:7,6,8,9,8,7,10,m.若去掉m,该组数据的下四分位数保持不变,则整数的值可以是____________.(写出一个满足条件的m值即可)
15.的展开式中,有理项是____________.(用关于x的式子表示)
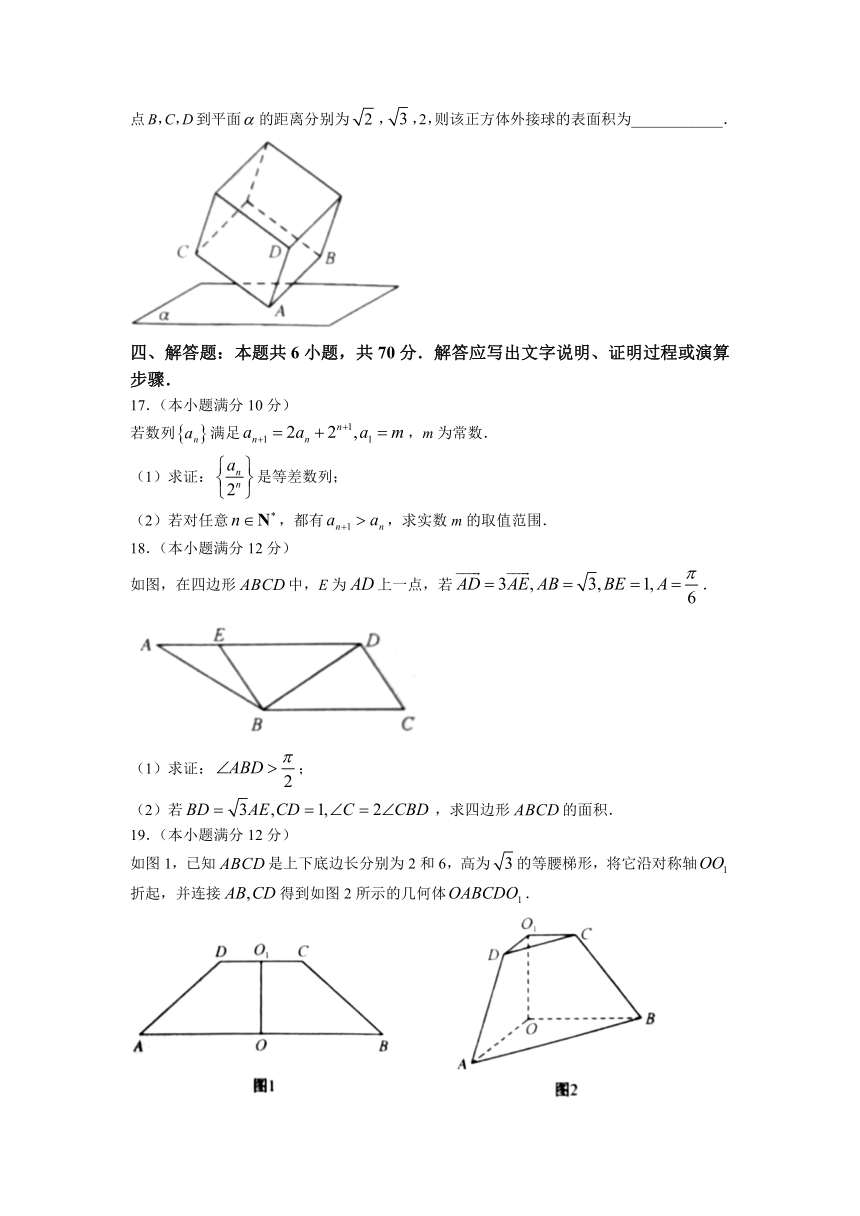
16.如图,某正方体的顶点A在平面内,三条棱都在平面的同侧.若顶点B,C,D到平面的距离分别为,,2,则该正方体外接球的表面积为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
若数列满足,m为常数.
(1)求证:是等差数列;
(2)若对任意,都有,求实数m的取值范围.
18.(本小题满分12分)
如图,在四边形中,E为上一点,若.
(1)求证:;
(2)若,求四边形的面积.
19.(本小题满分12分)
如图1,已知是上下底边长分别为2和6,高为的等腰梯形,将它沿对称轴折起,并连接得到如图2所示的几何体.
(1)判断几何体是哪种简单几何体,并证明;
(2)在几何体中,若二面角为直二面角,求二面角的余弦值.
20.(本小题满分12分)
2022年11月21日,我国迄今水下考古发现的体量最大的木质沉船长江口二号古船,在长江口横沙水域成功整体打捞出水,上海市文物局会同交通运输部上海打捞局,集成先进的打捞工艺、技术路线、设备制造,最终研究并形成了世界首创的“弧形梁非接触文物整体迁移技术”来打捞这艘古船.这是全新的打捞解决方案,创造性地融合了核电弧形梁加工工艺、隧道盾构掘进工艺、沉管隧道对接工艺,并运用液压同步提升技术,综合监控系统等先进的高新技术.这些技术也是首次应用于文物保护和考古领域.
近年来,随着科学技术的发展,越来越多的古迹具备了发掘的条件,然而相关考古专业人才却严重不足.某调查机构为了解高三学生在志愿填报时对考古专业的态度,在某中学高三年级的1200名男生和800名女生中按比例分配的分层,随机抽取20名学生进行了调查,调查结果如下表:
不填报 填报
非第一志愿填报 第一志愿填报
男生 x 5 2
女生 y 1 0
(1)完成列联表,并依据小概率值的独立性检验判断是否可以认为该校学生填报志愿时“是否填报考古专业”与性别有关联?
男生 女生 总计
不填报
填报
总计 20
(2)从抽出的男生中再随机抽取3人进一步了解情况,记X为抽取的这3名男生中“第一志愿填报考古专业”和“非第一志愿填报考古专业”人数差的绝对值,求X的数学期望.
附:.
0.05 0.010 0.001
3.841 6.635 10.828
21.(本小题满分12分)
设函数.
(1)当时,求曲线在点处的切线方程;
(2)若,且在区间上有极值,求实数a的取值范围.
22.(本小题满分12分)
在平面直角坐标系中,点P到点的距离比到y轴的距离大1,记点P的轨迹为曲线C.
(1)求C的方程;
(2)设过点F且不与x轴重合的直线l与C交于A,B两点,求证:在曲线C上存在点P,使得直线的斜率成等差数列.
高三数学参考答案、提示及评分细则
1.A 因为,所以.故选A.
2.A “这四个点中有三点在同一直线上”,一定能推出“这四点在同一个平面内”,充分性成立;“四个点在同一平面内”不能推出有三点在同一直线上,必要性不成立,所以前者是后者的充分不必要条件.故选A.
3.B 由,得渐近线方程为,又双曲线的两条新近线互相垂直,所以,解得.故选B.
4.D 因为,即,所以,故选D.
5.C 设,则.所以.
法一:因为,所以,即.
当时,,即,有两组满足条件
当时,或,所以但时,不符合题意,
故选C.
法二:如图,可转化为研究圆面内(包括边界)的整点个数.圆面包括的整点分别为,而不适合,则符合题意的整点共有4个.故选C.
6.B 因为,所以0不是的零点.当时,方程的解的个数为函数与的图象在上交点的个数,在同一坐标系中作出与在上的图象(注意到当时,单调递减,),如图所示,由图可知在区间上,两函数图象有4个交点,而与均为奇函数,故在上两图象交点个数为8,即在区间上的零点个数为8.故选B.
7.D 函数的图象与曲线关于直线对称,将的图象向下平移4个单位长度得到的图象,将的图象向左平移1个单位长度得到的图象,即,故.故选D.
8.C 设的中点为M,则,所以,所以外心O与中点M重合,故是以A为直角顶点的直角三角形.
法一:在上的投影向量为,所以,又.故选C.
法二:因为在上的投影向量为,所以在上的投影向量为,而,则.故选C.
9.BC 因为函数的最小正周期为,所以,则,所以.
对于A,法一:,,,则A错误;
法二:意味着的图象关于直线对称,将代入,得的图象关于点对称,则A错误;
对于B,,则B正确;
对于C,,,则C正确;
对于D,,当,即时,,使得;当,即时,,使得.所以在上,有两解,则D错误.故选BC.
10.ABD 由题意,,所以,所以,则A,D错误;,则B错误;,则C正确.故选ABD.
11.ACD 对于A.因为,所以,即,则A正确;
对于B,令,则,所以在上单调递增;由,得,所以,即,所以,则B错误;
对于C,因为,所以,所以,则C正确;
对于D,因为,所以,则D正确.故选ACD.
12.ABD 根据题意,且,即,显然当时,不满足C的方程;当时,两边平方化简,得,曲线C表示椭圆在第一象限和第三象限内的部分及坐标轴上的点,如下图所示:
用分别代替x,y,C的方程不变,所以曲线C关于原点对称.故A正确;
设,则.由,得,所以.故B正确;
对于C,曲线C与坐标轴所围成的图形如下图阴影部分所示(是曲线与坐标轴交点),
以为邻边作矩形,则阴影部分的面积,故C错误;
对于D,易知直线在曲线C上方,且没有公共点.设,与联立消去y,得,若直线与椭圆C相切,则,解得;当时,切点在第一象限,所以直线与直线间的距离即为的最小值,即,所以,故D正确.故选ABD.
13.2 由题意,得圆C的圆心,半径,直线l过定点,点P在圆C内.所以当时,取得最小值,此时的斜率,故l的斜率为2.
14.7(或8或9或10) 去掉m后的七个数从小到大排列为6,7,7,8,8,9,10,下四分位数就是第二个数7,且第2个数和第3个数都是7;而八个数的下四分位数是从小到大排列后,第二个数和第三个数的平均值,所以只要全部八个数从小到大排列后第2个数和第3个数就都还是7,下四分位数就不会变.所以整数m的值可以是7,或8,或9,或10.
15.和 展开式的通项为,由,得或8,,故有理项是和.
16. 法一:设正方体的棱长为a,取空间的一个基底,设是平面的一个方向向上的单位法向量.由空间向量基本定理,存在唯一的有序实数组,使得.由题意,在方向上的投影向量的长度分别为,,2.于是,,即,即,即.同理,.从而.由,得,即,解得,所以正方体的外接球半径为,外接球的表面积为.
法二:如图,连结,过A向上作平面的垂线段,接下来以为一条体对角线,同时将顶点A处的三条棱放在正方体的棱上作一个长方体,是长方体的三条棱(图略),则,则.作于,于,于;连结,令,由,可得,设正方体的棱长为a,因为,所以,解得,故该正方休外接球半径为,外接球的表面积为.
17.(1)证明:因为,
等式两边同除以,得,即,
所以数列是首项为,公差为1的等差数列.
(2)解:由(1)得,因此.
由对恒成立,得对均成立.
因为,不等式两边同除以,得,
即对恒成立,
当时,取最大值,所以,
所以实数m的取值范围为.
18.(1)证明:在中,由余弦定理,得,即,解得或2.
当时,由,得.
在中,由余弦定理,得,
所以.
此时.
当时,由,得.
在中,由余弦定理,得,
所以,
又,所以.
综上,.
(2)解:因为,结合(1)得.
设,则,
在中,由正弦定理,得,
即,
所以,
由,可得,所以,得,
则,所以四边形的面积.
19.(1)解:几何体是三棱台,证明如下:
由条件知,又平面平面,
所以平面,同理,平面.
因为,所以平面平面.
另一方面,延长交于点M,如图,
因为且,
所以,解得.
同理,延长交于点,也可得,
故点M和点重合,即延长后交于同一点M,
从而几何体是三棱台.
(2)解:因为,
所以是直二面角的一个平面角,
从而.
以O为原点,所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则.
所以,
所以,又因为,所以.
而平面,
所以平面是平面的一个法向量.
设是平面的一个法向量,
由及得
取,得.
设二面角的大小为,由图可知,为锐角,
所以,
即二面角的余弦值是.
20.解:(1)设抽取的20人中,男、女生人数分别为,则
所以.
列联表如下:
男生 女生 总计
不填报 5 7 12
填报 7 1 8
总计 12 8 20
零假设为:“是否填报考古专业”与性别无关联.
根据列联表中的数据,经计算得到.
根据小概率值的独立性检验,我们推断不成立,即认为“是否填报考古专业”与性别有关联,此推断犯错误的概率不大于0.05.
(2)X的可能取值为0,1,2,3,
;
;
;
.
所以.
21.解:(1)当时,,
则,切点为.
,切线斜率为,
所以所求切线方程为,即.
(2)法一:,
令,
因为,所以在R上单调递减;
又当时,,
所以,
又,
所以,使得.
所以,
因为,所以,由题意.
故当时,单调递增;
当时,单调递减,
在处取得极大值,.
令,则,
所以在上单调递增,
而,
所以,
故实数a的取值范围为.
法二:由题意,在上有零点,
即函数在上有零点,
即方程在上有实根.
令,则.
考虑到,则;,
所以在上单调递增,在上单调递减.
所以是的最大值点,即.
又,当,
函数的图象见如图.
由题意,,即.
当时,设,使.
当时,,
即单调递增;
当时,单调递减,
所以,且是的极值点.
故所求实数a的取值范围是.
22.(1)解:设,
由题意,得,
两边平方并整理,得.
故所求C的方程为.
(2)证明:C的方程为
当直线l的斜率不存在时,点A,B关于x轴对称,存在C上的点,使,显然直线的斜率成等差数列;
当直线l的斜率存在且不为0时,可设直线l的方程为,
联立消去x,得.
设,则.
若存在点满足条件,则,
即,
因为点P,A,B均在抛物线上,所以.
所以,
将代入得,整理得,
因为,所以,
代入,得.
此时,存在C上的点,使得直线的斜率成等差数列.
综上,存在C上的点P使得直线的斜率成等差数列.
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本卷命题范围:高考范围.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,则( )
A. B. C. D.
2.已知空间四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面内”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若双曲线的两条渐近线互相垂直,则( )
A. B. C.2 D.
4.已知,则( )
A. B. C. D.
5.已知复数z的实部和虚部均为整数,则满足的复数z的个数为( )
A.2 B.3 C.4 D.5
6.函数在区间上的零点个数为( )
A.10 B.8 C.6 D.4
7.将函数的图象向右平移1个单位长度后,再向上平移4个单位长度,所得函数图象与曲线关于直线对称,则( )
A. B. C. D.4
8.已知O是的外心,且满足,若在上的投影向量为,则( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.若函数的最小正周期为,则( )
A. B.的图象与函数的图象重合
C. D.存在唯一的,使得
10.设A,B是两个随机事件,且,若B发生时A必定发生,则下列结论错误的是( )
A. B. C. D.
11.已知,若,则( )
A. B. C. D.
12.已知曲线C的方程为,点P在C上,O为坐标原点,则( )
A.曲线C关于原点对称
B.
C.设C与坐标轴所围成图形的面积为S,则
D.若M是直线上的一点,则
三、填空题:本题共4小题,每小题5分,共20分.
13.若直线与圆相交于A,B两点,当取得最小值时,直线l的斜率为____________.
14.2022年9月19日,航天科技集团五院发布消息称,近日在法国巴黎召开的第73届国际宇航大会上,我国火星探测天问一号任务团队首次获得国际宇航联合会2022年度世界航天奖.为科普航天知识,某校组织学生参与航天知识竞答活动,某班8位同学的得分成绩如下:7,6,8,9,8,7,10,m.若去掉m,该组数据的下四分位数保持不变,则整数的值可以是____________.(写出一个满足条件的m值即可)
15.的展开式中,有理项是____________.(用关于x的式子表示)
16.如图,某正方体的顶点A在平面内,三条棱都在平面的同侧.若顶点B,C,D到平面的距离分别为,,2,则该正方体外接球的表面积为____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
若数列满足,m为常数.
(1)求证:是等差数列;
(2)若对任意,都有,求实数m的取值范围.
18.(本小题满分12分)
如图,在四边形中,E为上一点,若.
(1)求证:;
(2)若,求四边形的面积.
19.(本小题满分12分)
如图1,已知是上下底边长分别为2和6,高为的等腰梯形,将它沿对称轴折起,并连接得到如图2所示的几何体.
(1)判断几何体是哪种简单几何体,并证明;
(2)在几何体中,若二面角为直二面角,求二面角的余弦值.
20.(本小题满分12分)
2022年11月21日,我国迄今水下考古发现的体量最大的木质沉船长江口二号古船,在长江口横沙水域成功整体打捞出水,上海市文物局会同交通运输部上海打捞局,集成先进的打捞工艺、技术路线、设备制造,最终研究并形成了世界首创的“弧形梁非接触文物整体迁移技术”来打捞这艘古船.这是全新的打捞解决方案,创造性地融合了核电弧形梁加工工艺、隧道盾构掘进工艺、沉管隧道对接工艺,并运用液压同步提升技术,综合监控系统等先进的高新技术.这些技术也是首次应用于文物保护和考古领域.
近年来,随着科学技术的发展,越来越多的古迹具备了发掘的条件,然而相关考古专业人才却严重不足.某调查机构为了解高三学生在志愿填报时对考古专业的态度,在某中学高三年级的1200名男生和800名女生中按比例分配的分层,随机抽取20名学生进行了调查,调查结果如下表:
不填报 填报
非第一志愿填报 第一志愿填报
男生 x 5 2
女生 y 1 0
(1)完成列联表,并依据小概率值的独立性检验判断是否可以认为该校学生填报志愿时“是否填报考古专业”与性别有关联?
男生 女生 总计
不填报
填报
总计 20
(2)从抽出的男生中再随机抽取3人进一步了解情况,记X为抽取的这3名男生中“第一志愿填报考古专业”和“非第一志愿填报考古专业”人数差的绝对值,求X的数学期望.
附:.
0.05 0.010 0.001
3.841 6.635 10.828
21.(本小题满分12分)
设函数.
(1)当时,求曲线在点处的切线方程;
(2)若,且在区间上有极值,求实数a的取值范围.
22.(本小题满分12分)
在平面直角坐标系中,点P到点的距离比到y轴的距离大1,记点P的轨迹为曲线C.
(1)求C的方程;
(2)设过点F且不与x轴重合的直线l与C交于A,B两点,求证:在曲线C上存在点P,使得直线的斜率成等差数列.
高三数学参考答案、提示及评分细则
1.A 因为,所以.故选A.
2.A “这四个点中有三点在同一直线上”,一定能推出“这四点在同一个平面内”,充分性成立;“四个点在同一平面内”不能推出有三点在同一直线上,必要性不成立,所以前者是后者的充分不必要条件.故选A.
3.B 由,得渐近线方程为,又双曲线的两条新近线互相垂直,所以,解得.故选B.
4.D 因为,即,所以,故选D.
5.C 设,则.所以.
法一:因为,所以,即.
当时,,即,有两组满足条件
当时,或,所以但时,不符合题意,
故选C.
法二:如图,可转化为研究圆面内(包括边界)的整点个数.圆面包括的整点分别为,而不适合,则符合题意的整点共有4个.故选C.
6.B 因为,所以0不是的零点.当时,方程的解的个数为函数与的图象在上交点的个数,在同一坐标系中作出与在上的图象(注意到当时,单调递减,),如图所示,由图可知在区间上,两函数图象有4个交点,而与均为奇函数,故在上两图象交点个数为8,即在区间上的零点个数为8.故选B.
7.D 函数的图象与曲线关于直线对称,将的图象向下平移4个单位长度得到的图象,将的图象向左平移1个单位长度得到的图象,即,故.故选D.
8.C 设的中点为M,则,所以,所以外心O与中点M重合,故是以A为直角顶点的直角三角形.
法一:在上的投影向量为,所以,又.故选C.
法二:因为在上的投影向量为,所以在上的投影向量为,而,则.故选C.
9.BC 因为函数的最小正周期为,所以,则,所以.
对于A,法一:,,,则A错误;
法二:意味着的图象关于直线对称,将代入,得的图象关于点对称,则A错误;
对于B,,则B正确;
对于C,,,则C正确;
对于D,,当,即时,,使得;当,即时,,使得.所以在上,有两解,则D错误.故选BC.
10.ABD 由题意,,所以,所以,则A,D错误;,则B错误;,则C正确.故选ABD.
11.ACD 对于A.因为,所以,即,则A正确;
对于B,令,则,所以在上单调递增;由,得,所以,即,所以,则B错误;
对于C,因为,所以,所以,则C正确;
对于D,因为,所以,则D正确.故选ACD.
12.ABD 根据题意,且,即,显然当时,不满足C的方程;当时,两边平方化简,得,曲线C表示椭圆在第一象限和第三象限内的部分及坐标轴上的点,如下图所示:
用分别代替x,y,C的方程不变,所以曲线C关于原点对称.故A正确;
设,则.由,得,所以.故B正确;
对于C,曲线C与坐标轴所围成的图形如下图阴影部分所示(是曲线与坐标轴交点),
以为邻边作矩形,则阴影部分的面积,故C错误;
对于D,易知直线在曲线C上方,且没有公共点.设,与联立消去y,得,若直线与椭圆C相切,则,解得;当时,切点在第一象限,所以直线与直线间的距离即为的最小值,即,所以,故D正确.故选ABD.
13.2 由题意,得圆C的圆心,半径,直线l过定点,点P在圆C内.所以当时,取得最小值,此时的斜率,故l的斜率为2.
14.7(或8或9或10) 去掉m后的七个数从小到大排列为6,7,7,8,8,9,10,下四分位数就是第二个数7,且第2个数和第3个数都是7;而八个数的下四分位数是从小到大排列后,第二个数和第三个数的平均值,所以只要全部八个数从小到大排列后第2个数和第3个数就都还是7,下四分位数就不会变.所以整数m的值可以是7,或8,或9,或10.
15.和 展开式的通项为,由,得或8,,故有理项是和.
16. 法一:设正方体的棱长为a,取空间的一个基底,设是平面的一个方向向上的单位法向量.由空间向量基本定理,存在唯一的有序实数组,使得.由题意,在方向上的投影向量的长度分别为,,2.于是,,即,即,即.同理,.从而.由,得,即,解得,所以正方体的外接球半径为,外接球的表面积为.
法二:如图,连结,过A向上作平面的垂线段,接下来以为一条体对角线,同时将顶点A处的三条棱放在正方体的棱上作一个长方体,是长方体的三条棱(图略),则,则.作于,于,于;连结,令,由,可得,设正方体的棱长为a,因为,所以,解得,故该正方休外接球半径为,外接球的表面积为.
17.(1)证明:因为,
等式两边同除以,得,即,
所以数列是首项为,公差为1的等差数列.
(2)解:由(1)得,因此.
由对恒成立,得对均成立.
因为,不等式两边同除以,得,
即对恒成立,
当时,取最大值,所以,
所以实数m的取值范围为.
18.(1)证明:在中,由余弦定理,得,即,解得或2.
当时,由,得.
在中,由余弦定理,得,
所以.
此时.
当时,由,得.
在中,由余弦定理,得,
所以,
又,所以.
综上,.
(2)解:因为,结合(1)得.
设,则,
在中,由正弦定理,得,
即,
所以,
由,可得,所以,得,
则,所以四边形的面积.
19.(1)解:几何体是三棱台,证明如下:
由条件知,又平面平面,
所以平面,同理,平面.
因为,所以平面平面.
另一方面,延长交于点M,如图,
因为且,
所以,解得.
同理,延长交于点,也可得,
故点M和点重合,即延长后交于同一点M,
从而几何体是三棱台.
(2)解:因为,
所以是直二面角的一个平面角,
从而.
以O为原点,所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
则.
所以,
所以,又因为,所以.
而平面,
所以平面是平面的一个法向量.
设是平面的一个法向量,
由及得
取,得.
设二面角的大小为,由图可知,为锐角,
所以,
即二面角的余弦值是.
20.解:(1)设抽取的20人中,男、女生人数分别为,则
所以.
列联表如下:
男生 女生 总计
不填报 5 7 12
填报 7 1 8
总计 12 8 20
零假设为:“是否填报考古专业”与性别无关联.
根据列联表中的数据,经计算得到.
根据小概率值的独立性检验,我们推断不成立,即认为“是否填报考古专业”与性别有关联,此推断犯错误的概率不大于0.05.
(2)X的可能取值为0,1,2,3,
;
;
;
.
所以.
21.解:(1)当时,,
则,切点为.
,切线斜率为,
所以所求切线方程为,即.
(2)法一:,
令,
因为,所以在R上单调递减;
又当时,,
所以,
又,
所以,使得.
所以,
因为,所以,由题意.
故当时,单调递增;
当时,单调递减,
在处取得极大值,.
令,则,
所以在上单调递增,
而,
所以,
故实数a的取值范围为.
法二:由题意,在上有零点,
即函数在上有零点,
即方程在上有实根.
令,则.
考虑到,则;,
所以在上单调递增,在上单调递减.
所以是的最大值点,即.
又,当,
函数的图象见如图.
由题意,,即.
当时,设,使.
当时,,
即单调递增;
当时,单调递减,
所以,且是的极值点.
故所求实数a的取值范围是.
22.(1)解:设,
由题意,得,
两边平方并整理,得.
故所求C的方程为.
(2)证明:C的方程为
当直线l的斜率不存在时,点A,B关于x轴对称,存在C上的点,使,显然直线的斜率成等差数列;
当直线l的斜率存在且不为0时,可设直线l的方程为,
联立消去x,得.
设,则.
若存在点满足条件,则,
即,
因为点P,A,B均在抛物线上,所以.
所以,
将代入得,整理得,
因为,所以,
代入,得.
此时,存在C上的点,使得直线的斜率成等差数列.
综上,存在C上的点P使得直线的斜率成等差数列.
同课章节目录
