人教版2023年九年级(下)开学考试模拟练习卷(至九下第26章)(含解析)
文档属性
| 名称 | 人教版2023年九年级(下)开学考试模拟练习卷(至九下第26章)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 546.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 07:24:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2023年九年级(下)开学考试模拟练习卷
(满分120分)
一.选择题(共10小题,满分30分,每小题3分)
1.垃圾分类一小步,低碳生活一大步,垃圾桶上常有以下四种垃圾分类标识的图案和文字说明,其中图案是中心对称图形的是( )
A.有害垃圾B.厨余垃圾 C.其它垃圾 D.可回收物
2.用配方法解一元二次方程x2﹣6x+1=0,此方程可化为( )
A.(x﹣3)2=8 B.(x+3)2=8 C.(x+3)2=3 D.(x﹣3)2=3
3.如果将抛物线y=(x+1)2﹣1向上平移2个单位,那么平移后抛物线的顶点坐标是( )
A.(0,2) B.(2,0) C.(1,1) D.(﹣1,1)
4.已知反比例函数y=的图象在第一、三象限内,则k( )
A.k>2 B.k≥2 C.k<2 D.k≤2
5.通过大量的掷图钉试验,发现钉尖朝上的频率稳定在0.75附近,则可估计钉尖朝上的概率为( )
A. B. C. D.
6.若关于x的一元二次方程有实数根,则实数k的取值范围是( )
A.k≤2 B.k<2 C.k<2且k≠0 D.k≤2且k≠0
7.如图,将钝角△ABC绕点A按逆时针方向旋转110°,得到△AB'C',连接BB',若AC'∥BB',则∠CAB'的大小为( )
A.75° B.70° C.65° D.60°
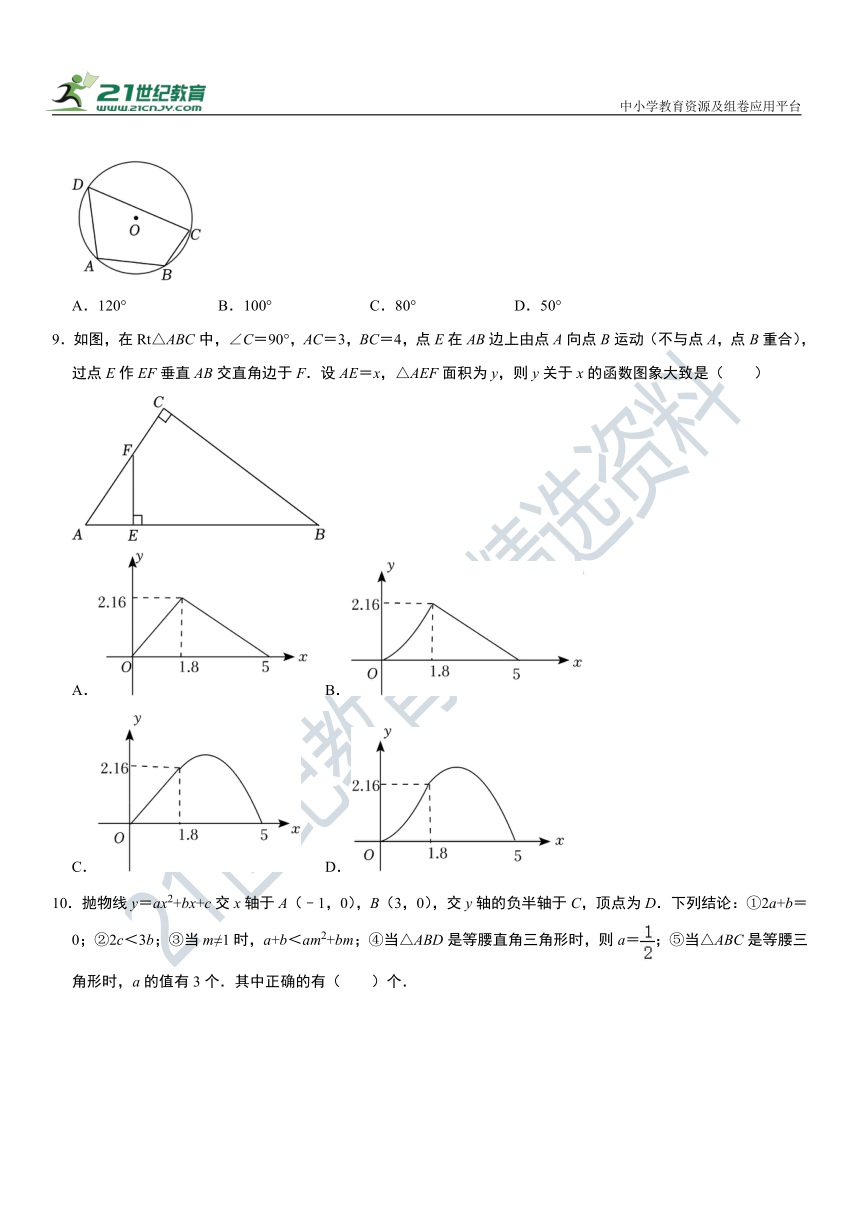
8.如图,四边形ABCD是⊙O的内接四边形,其中∠A=100°,则∠C的度数为( )
A.120° B.100° C.80° D.50°
9.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AB边上由点A向点B运动(不与点A,点B重合),过点E作EF垂直AB交直角边于F.设AE=x,△AEF面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
10.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5 B.4 C.3 D.2
二.填空题(共5小题,满分15分,每小题3分)
11.已知关于x的方程x2+kx﹣2=0的一个根是x=2,则另外一个根为 .
12.抛物线y=x2﹣2x﹣3的对称轴是直线 .
13.若点P(a﹣1,5)与点Q(5,1﹣b)关于原点成中心对称,则a+b= .
14.如图,PA、PB、DE分别切⊙O于点A、B、C,DE交PA、PB于点D、E,已知PA长8cm.则△PDE的周长为 .
15.如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=(x>0)的图象经过顶点B,则反比例函数的表达式为 .
三.解答题(共8小题,满分75分)
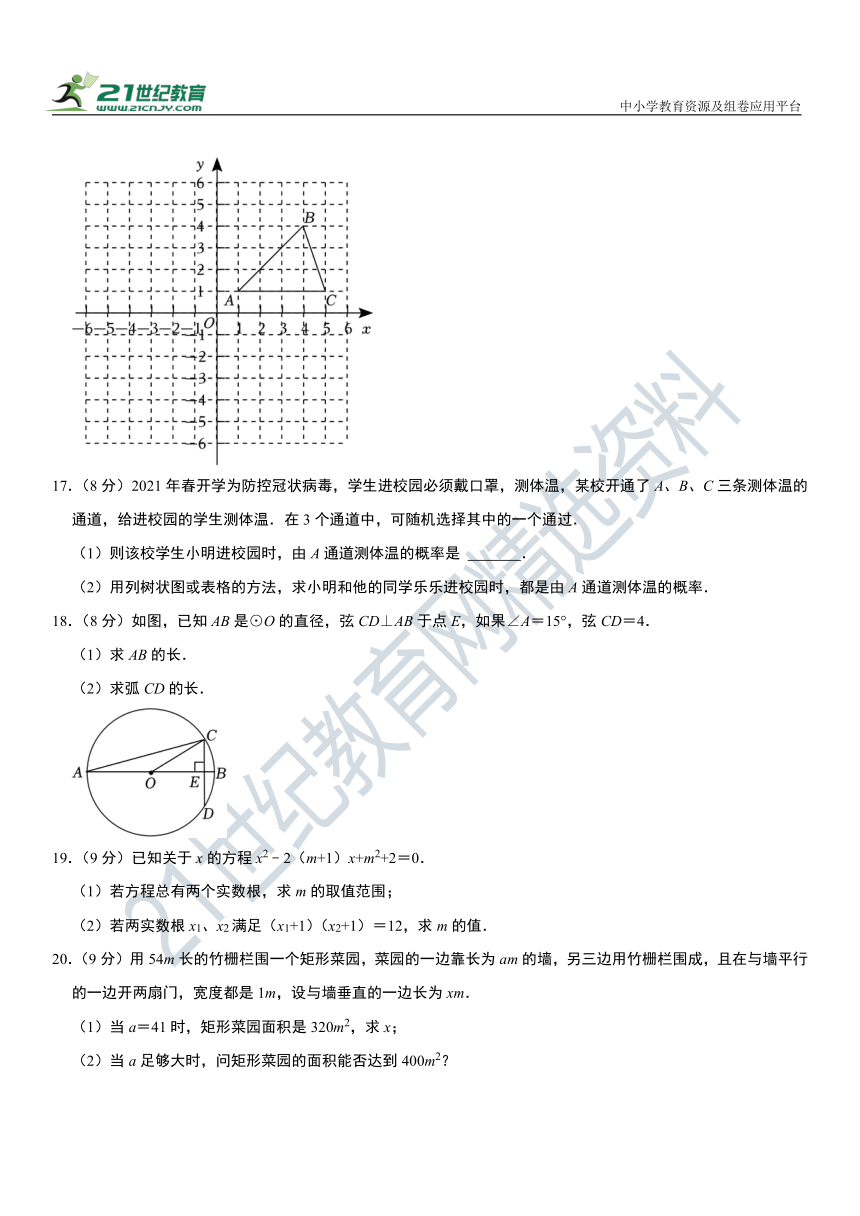
16.(8分)在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中A(1,1)、8(4,4)、C(5,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC关于原点O的中心对称图形,A,B、C的对称点分别是A2、B2、C2.
17.(8分)2021年春开学为防控冠状病毒,学生进校园必须戴口罩,测体温,某校开通了A、B、C三条测体温的通道,给进校园的学生测体温.在3个通道中,可随机选择其中的一个通过.
(1)则该校学生小明进校园时,由A通道测体温的概率是 .
(2)用列树状图或表格的方法,求小明和他的同学乐乐进校园时,都是由A通道测体温的概率.
18.(8分)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4.
(1)求AB的长.
(2)求弧CD的长.
19.(9分)已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若两实数根x1、x2满足(x1+1)(x2+1)=12,求m的值.
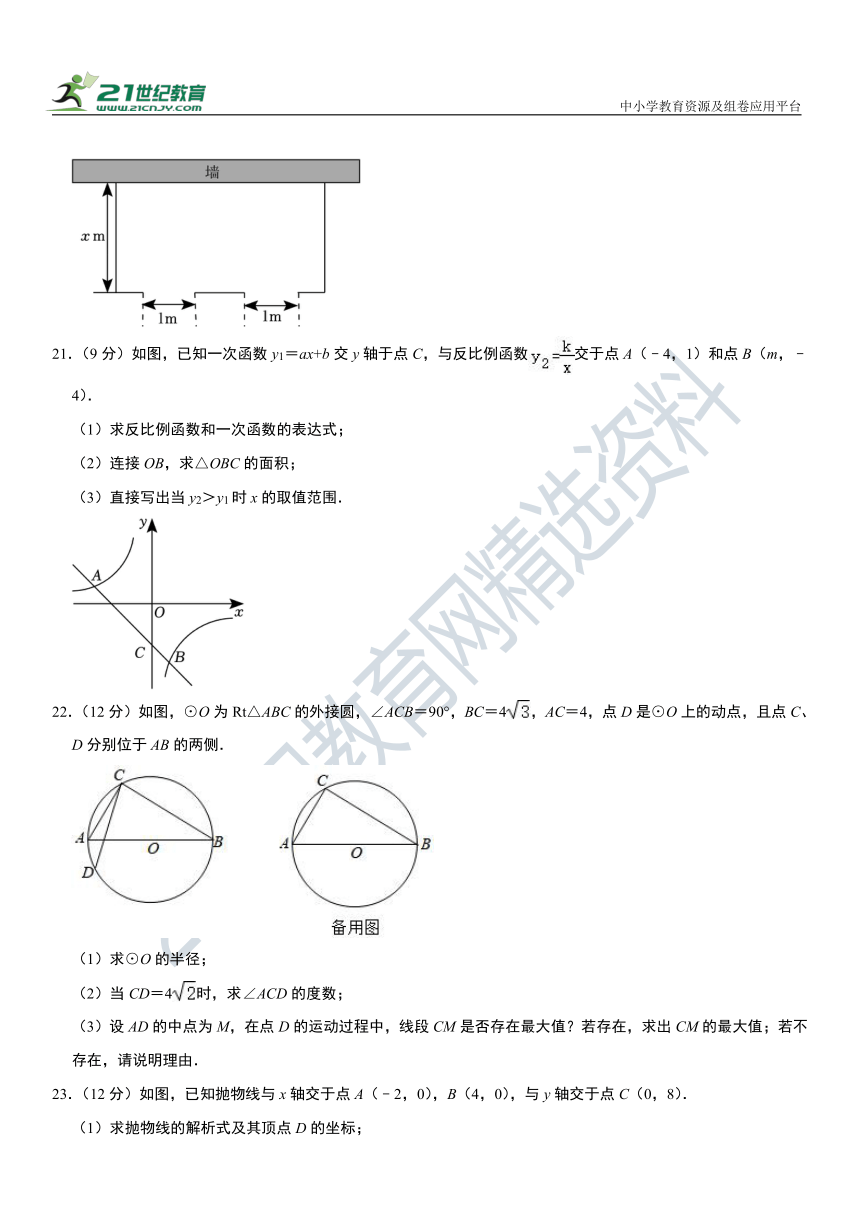
20.(9分)用54m长的竹栅栏围一个矩形菜园,菜园的一边靠长为am的墙,另三边用竹栅栏围成,且在与墙平行的一边开两扇门,宽度都是1m,设与墙垂直的一边长为xm.
(1)当a=41时,矩形菜园面积是320m2,求x;
(2)当a足够大时,问矩形菜园的面积能否达到400m2?
21.(9分)如图,已知一次函数y1=ax+b交y轴于点C,与反比例函数交于点A(﹣4,1)和点B(m,﹣4).
(1)求反比例函数和一次函数的表达式;
(2)连接OB,求△OBC的面积;
(3)直接写出当y2>y1时x的取值范围.
22.(12分)如图,⊙O为Rt△ABC的外接圆,∠ACB=90°,BC=4,AC=4,点D是⊙O上的动点,且点C、D分别位于AB的两侧.
(1)求⊙O的半径;
(2)当CD=4时,求∠ACD的度数;
(3)设AD的中点为M,在点D的运动过程中,线段CM是否存在最大值?若存在,求出CM的最大值;若不存在,请说明理由.
23.(12分)如图,已知抛物线与x轴交于点A(﹣2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A.是中心对称图形,故本选项符合题意;
B.不是中心对称图形,故本选项不合题意;
C.不是中心对称图形,故本选项不合题意;
D.不是中心对称图形,故本选项不符合题意.
故选:A.
2.【解答】解:x2﹣6x+1=0,
x2﹣6x=﹣1,
x2﹣6x+9=﹣1+9,即(x﹣3)2=8,
故选:A.
3.【解答】解:抛物线y=(x+1)2﹣1的顶点坐标为(﹣1,﹣1),
∵顶点坐标(﹣1,﹣1)向上平移2个单位,
∴平移后的抛物线的顶点坐标为(﹣1,1).
故选:D.
4.【解答】解:∵反比例函数y=的图象在第一、三象限内,
∴2﹣k>0,
∴k<2,
故选:C.
5.【解答】解:∵钉尖朝上的频率稳定在0.75附近,
∴可估计钉尖朝上的概率为.
故选:C.
6.【解答】解:∵关于x的一元二次方程kx2﹣2x+=0有实数根,
∴Δ=(﹣2)2﹣4k ≥0,
解得k≤2,
∵若关于x的一元二次方程,
∴k≠0,
∴k≤2且k≠0.
故选:D.
7.【解答】解:由旋转的性质可得AB=AB',∠BAB'=∠CAC'=110°,
∴,
∵AC∥BB',
∴∠C'AB'=∠AB'B=35°,
∴∠CAB'=∠CAC'﹣∠C'AB'=75°,故A正确.
故选:A.
8.【解答】解:∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,
∵∠A=100°,
∴∠C=180°﹣∠A=180°﹣100°=80°.
故选:C.
9.【解答】解:由题意得,AB==5,
当点C与点F重合时,EF=,此时AE=2.4×=1.8,
当0<x≤1.8时,y=,此抛物线开口方向向上;
当1.8<x<5时,y==,此抛物线开口方向向下;
故符合题意的图象是选项D.
故选:D.
10.【解答】解:①∵二次函数与x轴交于点A(﹣1,0)、B(3,0).
∴二次函数的对称轴为直线x==1,即﹣=1,
∴2a+b=0.
故①正确;
②∵二次函数y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0).
∴a﹣b+c=0,9a+3b+c=0.
又∵b=﹣2a.
∴3b=﹣6a,a﹣(﹣2a)+c=0.
∴3b=﹣6a,2c=﹣6a.
∴2c=3b.
故②错误;
③∵抛物线开口向上,对称轴是直线x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;
④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1﹣(﹣1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,﹣2).
∵二次函数的顶点D为(1,﹣2),过点A(﹣1,0).
设二次函数解析式为y=a(x﹣1)2﹣2.
∴0=a(﹣1﹣1)2﹣2.
解得a=.
故④正确;
⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.(故⑤错误)
故①③④正确,②⑤错误.
故选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:设方程的另一个根为t,
根据题意得2t=﹣2,解得t=﹣1.
即方程的另一个根为﹣1.
故答案为﹣1.
12.【解答】解:解法1:利用公式法
y=ax2+bx+c的顶点坐标公式为(,),代入数值求得对称轴是直线x=1;
解法2:利用配方法
y=x2﹣2x﹣3=x2﹣2x+1﹣4=(x﹣1)2﹣4,故对称轴是直线x=1.
故答案为:x=1.
13.【解答】解:∵点P(a﹣1,5)与点Q(5,1﹣b)关于原点成中心对称,
∴a﹣1=﹣5,1﹣b=﹣5,
解得a=﹣4,b=6,
∴a+b=﹣4+6=2.
故答案为:2.
14.【解答】解:∵PA、PB、DE是⊙O的切线,
∴DA=DC,EC=EB,
∴△PDE的周长=PD+DC+EC+PE=PA+PB=2PA=16(cm).
故答案为:16cm.
15.【解答】解:∵A的坐标为(3,4),
∴OA==5,
∵四边形OABC为菱形,
∴AB=OA=5,AB∥OC,
∴B(8,4),
把B(8,4)代入y=得k=8×4=32,
∴反比例函数的表达式为y=(x>0).
故答案为y=(x>0).
三.解答题(共8小题,满分75分)
16.【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
17.【解答】解:(1)∵某校开通了A、B、C三条测体温的通道,给进校园的学生测体温,
∴该校学生小明进校园时,由A通道测体温的概率是,
故答案为:;
(2)画树状图如下:
共有9种等可能的结果,小明和他的同学乐乐进校园时,都是由A通道测体温的结果有1种,
∴小明和他的同学乐乐进校园时,都是由A通道测体温的概率为.
18.【解答】解:(1)∵CD⊥AB,
∴CE=DE=CD=2,∠OEC=90°,
∵∠BOC=2∠A=2×15°=30°,
∴OC=2CE=4,
∴AB=2OC=8;
(2)如图,连接OD,
∵OC=OD,CD⊥AB,
∴∠COD=2∠BOC=60°,
∴=π,
答:弧CD的长为π.
19.【解答】解:(1)Δ=[﹣2(m+1)]2﹣4(m2+2)=8m﹣4,
∵方程总有两个实数根,
∴8m﹣4≥0,
∴m≥.
(2)由(x1+1)(x2+1)=x1x2+(x1+x2)+1=12,
∵x1x2=2(m+1),x1x2=m2+2,
∴原式=m2+2+2(m+1)+1=12,
整理得m2+2m﹣7=0,
解得m=﹣1﹣2(舍)或m=﹣1+2.
20.【解答】解:设与墙垂直的一边长为xm,则与墙平行的一边长为(54﹣2x+2)m.
(1)依题意得:x(54﹣2x+2)=320,
整理得:x2﹣28x+160=0,
解得:x1=8,x2=20.
当x=8时,56﹣2x=40<41,符合题意;
当x=20时,56﹣2x=16<41,符合题意.
答:x的值为8或20.
(2)令x(54﹣2x+2)=400①,
整理得:x2﹣28x+200=0.
∵Δ=(﹣28)2﹣4×1×200=﹣16<0,
∴方程①无实数根,
∴矩形菜园的面积不能达到400m2.
21.【解答】解:(1)∵点A(﹣4,1)在反比例函数的图象上,
∴k=﹣4×1=﹣4,
∴反比例函数的表达式为y2=﹣,
∵点B(m,﹣4)也在反比例函数y2=﹣的图象上,
∴﹣4=﹣,解得m=1,
∴B(1,﹣4),
把点A(﹣4,1),点B(1,﹣4)代入一次函数y1=ax+b中,
得,
解得,
∴一次函数的表达式为y1=﹣x﹣3;
(2)令x=0,则y1=﹣x﹣3=﹣3,
∴C(0,﹣3),
∴S△OBC==;
(3)当y2>y1时x的取值范围是﹣4<x<0或x>1.
22.【解答】解:(1)如图1中,
∵AB是直径,
∴∠ACB=90°,
∵AC=4,BC=4,
∴AB===8,
∴⊙O的半径为4.
(2)如图1中,连接OC,OD.
∵CD=4,OC=OD=4,
∴CD2=OC2+OD2,
∴∠COD=90°,
∴∠OCD=45°,
∵AC=OC=OA,
∴△AOC是等边三角形,
∴∠ACO=60°,
∴∠ACD=∠ACO﹣∠DCO=60°﹣45°=15°.
(3)如图2中,连接OM,OC.
∵AM=MD,
∴OM⊥AD,
∴点M的运动轨迹以AO为直径的⊙J,
连接CJ,JM.
∵△AOC是等边三角形,AJ=OJ,
∴CJ⊥OA,
∴CJ==2,
∵CM≤CJ+JM=2+2,
∴CM的最大值为2+2.
23.【解答】解:(1)设抛物线解析式为y=a(x+2)(x﹣4).
把C(0,8)代入,得a=﹣1.
∴y=﹣x2+2x+8=﹣(x﹣1)2+9,
顶点D(1,9);(2分)
(2)假设满足条件的点P存在.依题意设P(2,t).
由C(0,8),D(1,9)求得直线CD的解析式为y=x+8,
它与x轴的夹角为45°.
设OB的中垂线交CD于H,则H(2,10).
则PH=|10﹣t|,点P到CD的距离为.
又.(4分)
∴.
平方并整理得:t2+20t﹣92=0,解之得t=﹣10±8.
∴存在满足条件的点P,P的坐标为(2,﹣10±8).(6分)
(3)由上求得E(﹣8,0),F(4,12).
①若抛物线向上平移,可设解析式为y=﹣x2+2x+8+m(m>0).
当x=﹣8时,y=﹣72+m.
当x=4时,y=m.
∴﹣72+m≤0或m≤12.
∴0<m≤72.(8分)
②若抛物线向下平移,可设解析式为y=﹣x2+2x+8﹣m(m>0).
由,
有﹣x2+x﹣m=0.
∴△=1﹣4m≥0,
∴m≤.
∴向上最多可平移72个单位长,向下最多可平移个单位长.(10分)
人教版2023年九年级(下)开学考试模拟练习卷
(满分120分)
一.选择题(共10小题,满分30分,每小题3分)
1.垃圾分类一小步,低碳生活一大步,垃圾桶上常有以下四种垃圾分类标识的图案和文字说明,其中图案是中心对称图形的是( )
A.有害垃圾B.厨余垃圾 C.其它垃圾 D.可回收物
2.用配方法解一元二次方程x2﹣6x+1=0,此方程可化为( )
A.(x﹣3)2=8 B.(x+3)2=8 C.(x+3)2=3 D.(x﹣3)2=3
3.如果将抛物线y=(x+1)2﹣1向上平移2个单位,那么平移后抛物线的顶点坐标是( )
A.(0,2) B.(2,0) C.(1,1) D.(﹣1,1)
4.已知反比例函数y=的图象在第一、三象限内,则k( )
A.k>2 B.k≥2 C.k<2 D.k≤2
5.通过大量的掷图钉试验,发现钉尖朝上的频率稳定在0.75附近,则可估计钉尖朝上的概率为( )
A. B. C. D.
6.若关于x的一元二次方程有实数根,则实数k的取值范围是( )
A.k≤2 B.k<2 C.k<2且k≠0 D.k≤2且k≠0
7.如图,将钝角△ABC绕点A按逆时针方向旋转110°,得到△AB'C',连接BB',若AC'∥BB',则∠CAB'的大小为( )
A.75° B.70° C.65° D.60°
8.如图,四边形ABCD是⊙O的内接四边形,其中∠A=100°,则∠C的度数为( )
A.120° B.100° C.80° D.50°
9.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AB边上由点A向点B运动(不与点A,点B重合),过点E作EF垂直AB交直角边于F.设AE=x,△AEF面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
10.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5 B.4 C.3 D.2
二.填空题(共5小题,满分15分,每小题3分)
11.已知关于x的方程x2+kx﹣2=0的一个根是x=2,则另外一个根为 .
12.抛物线y=x2﹣2x﹣3的对称轴是直线 .
13.若点P(a﹣1,5)与点Q(5,1﹣b)关于原点成中心对称,则a+b= .
14.如图,PA、PB、DE分别切⊙O于点A、B、C,DE交PA、PB于点D、E,已知PA长8cm.则△PDE的周长为 .
15.如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=(x>0)的图象经过顶点B,则反比例函数的表达式为 .
三.解答题(共8小题,满分75分)
16.(8分)在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中A(1,1)、8(4,4)、C(5,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC关于原点O的中心对称图形,A,B、C的对称点分别是A2、B2、C2.
17.(8分)2021年春开学为防控冠状病毒,学生进校园必须戴口罩,测体温,某校开通了A、B、C三条测体温的通道,给进校园的学生测体温.在3个通道中,可随机选择其中的一个通过.
(1)则该校学生小明进校园时,由A通道测体温的概率是 .
(2)用列树状图或表格的方法,求小明和他的同学乐乐进校园时,都是由A通道测体温的概率.
18.(8分)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4.
(1)求AB的长.
(2)求弧CD的长.
19.(9分)已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若两实数根x1、x2满足(x1+1)(x2+1)=12,求m的值.
20.(9分)用54m长的竹栅栏围一个矩形菜园,菜园的一边靠长为am的墙,另三边用竹栅栏围成,且在与墙平行的一边开两扇门,宽度都是1m,设与墙垂直的一边长为xm.
(1)当a=41时,矩形菜园面积是320m2,求x;
(2)当a足够大时,问矩形菜园的面积能否达到400m2?
21.(9分)如图,已知一次函数y1=ax+b交y轴于点C,与反比例函数交于点A(﹣4,1)和点B(m,﹣4).
(1)求反比例函数和一次函数的表达式;
(2)连接OB,求△OBC的面积;
(3)直接写出当y2>y1时x的取值范围.
22.(12分)如图,⊙O为Rt△ABC的外接圆,∠ACB=90°,BC=4,AC=4,点D是⊙O上的动点,且点C、D分别位于AB的两侧.
(1)求⊙O的半径;
(2)当CD=4时,求∠ACD的度数;
(3)设AD的中点为M,在点D的运动过程中,线段CM是否存在最大值?若存在,求出CM的最大值;若不存在,请说明理由.
23.(12分)如图,已知抛物线与x轴交于点A(﹣2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A.是中心对称图形,故本选项符合题意;
B.不是中心对称图形,故本选项不合题意;
C.不是中心对称图形,故本选项不合题意;
D.不是中心对称图形,故本选项不符合题意.
故选:A.
2.【解答】解:x2﹣6x+1=0,
x2﹣6x=﹣1,
x2﹣6x+9=﹣1+9,即(x﹣3)2=8,
故选:A.
3.【解答】解:抛物线y=(x+1)2﹣1的顶点坐标为(﹣1,﹣1),
∵顶点坐标(﹣1,﹣1)向上平移2个单位,
∴平移后的抛物线的顶点坐标为(﹣1,1).
故选:D.
4.【解答】解:∵反比例函数y=的图象在第一、三象限内,
∴2﹣k>0,
∴k<2,
故选:C.
5.【解答】解:∵钉尖朝上的频率稳定在0.75附近,
∴可估计钉尖朝上的概率为.
故选:C.
6.【解答】解:∵关于x的一元二次方程kx2﹣2x+=0有实数根,
∴Δ=(﹣2)2﹣4k ≥0,
解得k≤2,
∵若关于x的一元二次方程,
∴k≠0,
∴k≤2且k≠0.
故选:D.
7.【解答】解:由旋转的性质可得AB=AB',∠BAB'=∠CAC'=110°,
∴,
∵AC∥BB',
∴∠C'AB'=∠AB'B=35°,
∴∠CAB'=∠CAC'﹣∠C'AB'=75°,故A正确.
故选:A.
8.【解答】解:∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,
∵∠A=100°,
∴∠C=180°﹣∠A=180°﹣100°=80°.
故选:C.
9.【解答】解:由题意得,AB==5,
当点C与点F重合时,EF=,此时AE=2.4×=1.8,
当0<x≤1.8时,y=,此抛物线开口方向向上;
当1.8<x<5时,y==,此抛物线开口方向向下;
故符合题意的图象是选项D.
故选:D.
10.【解答】解:①∵二次函数与x轴交于点A(﹣1,0)、B(3,0).
∴二次函数的对称轴为直线x==1,即﹣=1,
∴2a+b=0.
故①正确;
②∵二次函数y=ax2+bx+c与x轴交于点A(﹣1,0)、B(3,0).
∴a﹣b+c=0,9a+3b+c=0.
又∵b=﹣2a.
∴3b=﹣6a,a﹣(﹣2a)+c=0.
∴3b=﹣6a,2c=﹣6a.
∴2c=3b.
故②错误;
③∵抛物线开口向上,对称轴是直线x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;
④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1﹣(﹣1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,﹣2).
∵二次函数的顶点D为(1,﹣2),过点A(﹣1,0).
设二次函数解析式为y=a(x﹣1)2﹣2.
∴0=a(﹣1﹣1)2﹣2.
解得a=.
故④正确;
⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.(故⑤错误)
故①③④正确,②⑤错误.
故选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.【解答】解:设方程的另一个根为t,
根据题意得2t=﹣2,解得t=﹣1.
即方程的另一个根为﹣1.
故答案为﹣1.
12.【解答】解:解法1:利用公式法
y=ax2+bx+c的顶点坐标公式为(,),代入数值求得对称轴是直线x=1;
解法2:利用配方法
y=x2﹣2x﹣3=x2﹣2x+1﹣4=(x﹣1)2﹣4,故对称轴是直线x=1.
故答案为:x=1.
13.【解答】解:∵点P(a﹣1,5)与点Q(5,1﹣b)关于原点成中心对称,
∴a﹣1=﹣5,1﹣b=﹣5,
解得a=﹣4,b=6,
∴a+b=﹣4+6=2.
故答案为:2.
14.【解答】解:∵PA、PB、DE是⊙O的切线,
∴DA=DC,EC=EB,
∴△PDE的周长=PD+DC+EC+PE=PA+PB=2PA=16(cm).
故答案为:16cm.
15.【解答】解:∵A的坐标为(3,4),
∴OA==5,
∵四边形OABC为菱形,
∴AB=OA=5,AB∥OC,
∴B(8,4),
把B(8,4)代入y=得k=8×4=32,
∴反比例函数的表达式为y=(x>0).
故答案为y=(x>0).
三.解答题(共8小题,满分75分)
16.【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
17.【解答】解:(1)∵某校开通了A、B、C三条测体温的通道,给进校园的学生测体温,
∴该校学生小明进校园时,由A通道测体温的概率是,
故答案为:;
(2)画树状图如下:
共有9种等可能的结果,小明和他的同学乐乐进校园时,都是由A通道测体温的结果有1种,
∴小明和他的同学乐乐进校园时,都是由A通道测体温的概率为.
18.【解答】解:(1)∵CD⊥AB,
∴CE=DE=CD=2,∠OEC=90°,
∵∠BOC=2∠A=2×15°=30°,
∴OC=2CE=4,
∴AB=2OC=8;
(2)如图,连接OD,
∵OC=OD,CD⊥AB,
∴∠COD=2∠BOC=60°,
∴=π,
答:弧CD的长为π.
19.【解答】解:(1)Δ=[﹣2(m+1)]2﹣4(m2+2)=8m﹣4,
∵方程总有两个实数根,
∴8m﹣4≥0,
∴m≥.
(2)由(x1+1)(x2+1)=x1x2+(x1+x2)+1=12,
∵x1x2=2(m+1),x1x2=m2+2,
∴原式=m2+2+2(m+1)+1=12,
整理得m2+2m﹣7=0,
解得m=﹣1﹣2(舍)或m=﹣1+2.
20.【解答】解:设与墙垂直的一边长为xm,则与墙平行的一边长为(54﹣2x+2)m.
(1)依题意得:x(54﹣2x+2)=320,
整理得:x2﹣28x+160=0,
解得:x1=8,x2=20.
当x=8时,56﹣2x=40<41,符合题意;
当x=20时,56﹣2x=16<41,符合题意.
答:x的值为8或20.
(2)令x(54﹣2x+2)=400①,
整理得:x2﹣28x+200=0.
∵Δ=(﹣28)2﹣4×1×200=﹣16<0,
∴方程①无实数根,
∴矩形菜园的面积不能达到400m2.
21.【解答】解:(1)∵点A(﹣4,1)在反比例函数的图象上,
∴k=﹣4×1=﹣4,
∴反比例函数的表达式为y2=﹣,
∵点B(m,﹣4)也在反比例函数y2=﹣的图象上,
∴﹣4=﹣,解得m=1,
∴B(1,﹣4),
把点A(﹣4,1),点B(1,﹣4)代入一次函数y1=ax+b中,
得,
解得,
∴一次函数的表达式为y1=﹣x﹣3;
(2)令x=0,则y1=﹣x﹣3=﹣3,
∴C(0,﹣3),
∴S△OBC==;
(3)当y2>y1时x的取值范围是﹣4<x<0或x>1.
22.【解答】解:(1)如图1中,
∵AB是直径,
∴∠ACB=90°,
∵AC=4,BC=4,
∴AB===8,
∴⊙O的半径为4.
(2)如图1中,连接OC,OD.
∵CD=4,OC=OD=4,
∴CD2=OC2+OD2,
∴∠COD=90°,
∴∠OCD=45°,
∵AC=OC=OA,
∴△AOC是等边三角形,
∴∠ACO=60°,
∴∠ACD=∠ACO﹣∠DCO=60°﹣45°=15°.
(3)如图2中,连接OM,OC.
∵AM=MD,
∴OM⊥AD,
∴点M的运动轨迹以AO为直径的⊙J,
连接CJ,JM.
∵△AOC是等边三角形,AJ=OJ,
∴CJ⊥OA,
∴CJ==2,
∵CM≤CJ+JM=2+2,
∴CM的最大值为2+2.
23.【解答】解:(1)设抛物线解析式为y=a(x+2)(x﹣4).
把C(0,8)代入,得a=﹣1.
∴y=﹣x2+2x+8=﹣(x﹣1)2+9,
顶点D(1,9);(2分)
(2)假设满足条件的点P存在.依题意设P(2,t).
由C(0,8),D(1,9)求得直线CD的解析式为y=x+8,
它与x轴的夹角为45°.
设OB的中垂线交CD于H,则H(2,10).
则PH=|10﹣t|,点P到CD的距离为.
又.(4分)
∴.
平方并整理得:t2+20t﹣92=0,解之得t=﹣10±8.
∴存在满足条件的点P,P的坐标为(2,﹣10±8).(6分)
(3)由上求得E(﹣8,0),F(4,12).
①若抛物线向上平移,可设解析式为y=﹣x2+2x+8+m(m>0).
当x=﹣8时,y=﹣72+m.
当x=4时,y=m.
∴﹣72+m≤0或m≤12.
∴0<m≤72.(8分)
②若抛物线向下平移,可设解析式为y=﹣x2+2x+8﹣m(m>0).
由,
有﹣x2+x﹣m=0.
∴△=1﹣4m≥0,
∴m≤.
∴向上最多可平移72个单位长,向下最多可平移个单位长.(10分)
同课章节目录
