7.1.2 平面直角坐标系
图片预览







文档简介
(共24张PPT)
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.2 平面直角坐标系
学习目标
1.理解平面直角坐标系及其相关概念.
2.理解平面直角坐标系的点与有序数对一一对应的关系.
3.能利用平面直角坐标系表示点的位置,也能根据坐标找到坐标平面上它所表示的点.
重点:平面直角坐标系及相关概念,各象限及坐标轴上点的坐标特征.
难点:建立适当的坐标系,表示平面上的点的坐标.
课前预习
阅读课本第P65-68页内容,学习本节主要内容.
水平的数轴
互相垂直,原点重合
取向右的方向
竖直的数轴
取向上的方向
原点
坐标轴
第一象限
第二象限
第三象限
第四象限
任何象限
新课导入
问题1 (1)你还记得数轴的三要素吗
(2)请画出一条数轴,并在上面分别标出表示 1和-3.5的点.
(3)分别写出数轴上点A、B表示的数.
答(1)原点、正方向、单位长度
(2)
(3)点A对应的数为-3
点B对应的数为2
-3.5
0
1
问题2 由问题1你发现数轴上的点与实数是什么关系?
①数轴上的每个点都对应一个实数(这个实数叫做这个
点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
一一对应
思考
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(如图A,B,C,D各点)?
利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
探究新知
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
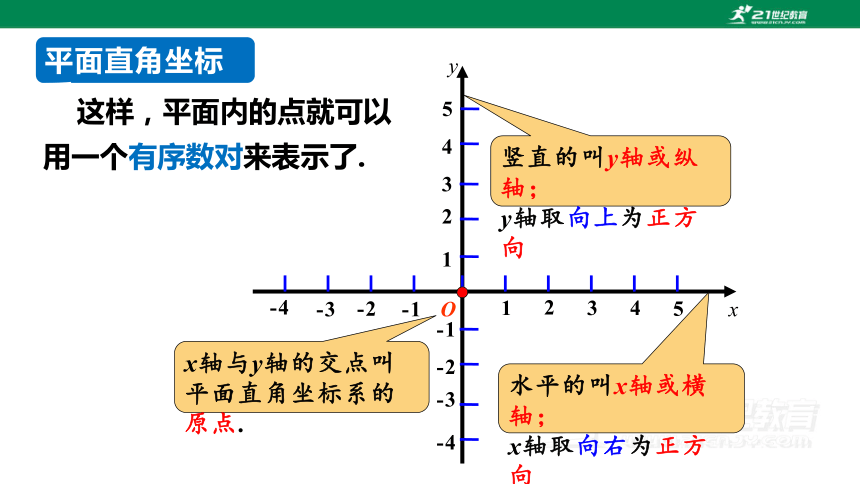
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
这样,平面内的点就可以用一个有序数对来表示了.
平面直角坐标系
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
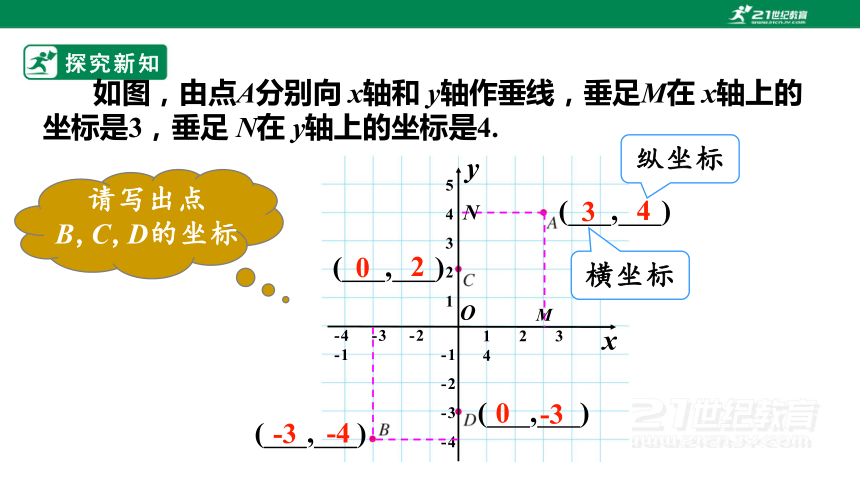
请写出点B,C,D的坐标
( , )
0
2
( , )
0
-3
如图,由点A分别向 x轴和 y轴作垂线,垂足M在 x轴上的坐标是3,垂足 N在 y轴上的坐标是4.
M
N
探究新知
在平面直角坐标系中:
①原点 O 的坐标为( , );
0
0
②x 轴上的点的 坐标为 ;
③y 轴上的点的 坐标为 .
0
纵
横
0
3
1
4
2
5
O
1
2
3
4
-4
-3
-2
-1
x
y
知识归纳
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个部分.每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
注意:坐标轴上的点不属于任何一个象限.
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
研究新知
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
例 在平面直角坐标系中描出下列各点:
A(4,5), B(-2,3),
C(-4,-1), D(2.5,-2),
E(0,-4).
.
A(4,5)
.
B(-2,3)
.
C(-4,-1)
.
D(2.5,-2)
.
E(0,-4)
各区域的点有什么特征呢?
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x 轴
y 轴
+
+
-
+
-
-
+
-
纵坐标为 0
横坐标为 0
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
知识归纳
思考:坐标平面内的点与有序数对(坐标)是什么关系
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
坐标平面内的点与有序实数是一一对应的
探究新知
例1 已知点P(a-3,a+2),若点P在x轴上,则a=_____;若点P在y轴上,则a=____;若连接点P,Q(3-a,a+2),则线段PQ与______(选填“x轴”或“y轴”)平行.
3
-2
x轴
例题分析
例2 在如图所示的平面直角坐标系中找出下列各点:A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4),F(3,0),G(0,1),H(-5,0).
解:如图所示.
y
x
O
1 2 3 4
5
4
3
2
1
-4
-2
-5
5
6
-3
-2
-1
-6
-1
-3
-4
A (4,5)
B (-2,3)
C (-4,-1)
D (2.5 , -2)
E (0, -4)
F (3, 0)
G (0, 1)
H (-5,0)
1.写出图中点 A,B,C,D,E,F 的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
解:如图所示
随堂练习
2.在图中描出下列各点:L(-5,-3), M(4,0), N(-6,2), P(5,-3.5), Q(0,5), R(6,2).
解:如图所示
y
x
O
1 2 3 4
5
4
3
2
1
-4
-2
-5
5
6
-3
-2
-1
-6
-1
-3
-4
L
.
M
.
N
.
.
Q
.
R
.
P
如图,正方形 ABCD 的边长为 6,如果以点 A 为原点,AB 所在的直线为 x轴建立平面直角坐标系,那么 y 轴在什么位置?写出正方形的顶点 A,B,C,D 的坐标.
y
x 轴与 y 轴交点为原点
(0,0)
(6,0)
(6,6)
(0,6)
C
D
x
A(O)
B
探究
解:如图所示
探究新知
(2)请另建立一个平面直角坐标系,此时正方形的顶点 A,B,C,D 的坐标又分别是什么?
y
A
B
C
D
O
(-3,-3)
(3,-3)
(3,3)
(-3,3)
解:如图所示
x
由前面得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.
思考
需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
3.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
4.已知A(-5,0),B(3,0),点C在y轴上,△ABC的面积为12,则点C的坐标为_____________________.
(0,3)或(0,-3)
随堂练习
5.如图,根据图中正方形的位置,分别写出边长为2的正方形ABCD的各点坐标.
解:(1)A(0,0),B(-2,0),C(-2,2),D(0,2);
(2)A(0,0),B(-2,0),C(-2,-2),D(0,-2);
(3)A(0,0),B(0,-2),C(2,-2),D(2,0).
平面直角坐标系及点的坐标
定义:原点、坐标轴
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
课堂小结
1.教材P69~70习题7.1第2,3,4,5,6题;
2.完成对应课时练习.
作业布置
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.2 平面直角坐标系
学习目标
1.理解平面直角坐标系及其相关概念.
2.理解平面直角坐标系的点与有序数对一一对应的关系.
3.能利用平面直角坐标系表示点的位置,也能根据坐标找到坐标平面上它所表示的点.
重点:平面直角坐标系及相关概念,各象限及坐标轴上点的坐标特征.
难点:建立适当的坐标系,表示平面上的点的坐标.
课前预习
阅读课本第P65-68页内容,学习本节主要内容.
水平的数轴
互相垂直,原点重合
取向右的方向
竖直的数轴
取向上的方向
原点
坐标轴
第一象限
第二象限
第三象限
第四象限
任何象限
新课导入
问题1 (1)你还记得数轴的三要素吗
(2)请画出一条数轴,并在上面分别标出表示 1和-3.5的点.
(3)分别写出数轴上点A、B表示的数.
答(1)原点、正方向、单位长度
(2)
(3)点A对应的数为-3
点B对应的数为2
-3.5
0
1
问题2 由问题1你发现数轴上的点与实数是什么关系?
①数轴上的每个点都对应一个实数(这个实数叫做这个
点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
一一对应
思考
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢(如图A,B,C,D各点)?
利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
探究新知
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
这样,平面内的点就可以用一个有序数对来表示了.
平面直角坐标系
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
请写出点B,C,D的坐标
( , )
0
2
( , )
0
-3
如图,由点A分别向 x轴和 y轴作垂线,垂足M在 x轴上的坐标是3,垂足 N在 y轴上的坐标是4.
M
N
探究新知
在平面直角坐标系中:
①原点 O 的坐标为( , );
0
0
②x 轴上的点的 坐标为 ;
③y 轴上的点的 坐标为 .
0
纵
横
0
3
1
4
2
5
O
1
2
3
4
-4
-3
-2
-1
x
y
知识归纳
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个部分.每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
注意:坐标轴上的点不属于任何一个象限.
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
研究新知
x
y
O
1 2 3 4 5
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
-5
例 在平面直角坐标系中描出下列各点:
A(4,5), B(-2,3),
C(-4,-1), D(2.5,-2),
E(0,-4).
.
A(4,5)
.
B(-2,3)
.
C(-4,-1)
.
D(2.5,-2)
.
E(0,-4)
各区域的点有什么特征呢?
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x 轴
y 轴
+
+
-
+
-
-
+
-
纵坐标为 0
横坐标为 0
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
知识归纳
思考:坐标平面内的点与有序数对(坐标)是什么关系
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
坐标平面内的点与有序实数是一一对应的
探究新知
例1 已知点P(a-3,a+2),若点P在x轴上,则a=_____;若点P在y轴上,则a=____;若连接点P,Q(3-a,a+2),则线段PQ与______(选填“x轴”或“y轴”)平行.
3
-2
x轴
例题分析
例2 在如图所示的平面直角坐标系中找出下列各点:A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4),F(3,0),G(0,1),H(-5,0).
解:如图所示.
y
x
O
1 2 3 4
5
4
3
2
1
-4
-2
-5
5
6
-3
-2
-1
-6
-1
-3
-4
A (4,5)
B (-2,3)
C (-4,-1)
D (2.5 , -2)
E (0, -4)
F (3, 0)
G (0, 1)
H (-5,0)
1.写出图中点 A,B,C,D,E,F 的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
解:如图所示
随堂练习
2.在图中描出下列各点:L(-5,-3), M(4,0), N(-6,2), P(5,-3.5), Q(0,5), R(6,2).
解:如图所示
y
x
O
1 2 3 4
5
4
3
2
1
-4
-2
-5
5
6
-3
-2
-1
-6
-1
-3
-4
L
.
M
.
N
.
.
Q
.
R
.
P
如图,正方形 ABCD 的边长为 6,如果以点 A 为原点,AB 所在的直线为 x轴建立平面直角坐标系,那么 y 轴在什么位置?写出正方形的顶点 A,B,C,D 的坐标.
y
x 轴与 y 轴交点为原点
(0,0)
(6,0)
(6,6)
(0,6)
C
D
x
A(O)
B
探究
解:如图所示
探究新知
(2)请另建立一个平面直角坐标系,此时正方形的顶点 A,B,C,D 的坐标又分别是什么?
y
A
B
C
D
O
(-3,-3)
(3,-3)
(3,3)
(-3,3)
解:如图所示
x
由前面得知,建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.
思考
需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
3.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
4.已知A(-5,0),B(3,0),点C在y轴上,△ABC的面积为12,则点C的坐标为_____________________.
(0,3)或(0,-3)
随堂练习
5.如图,根据图中正方形的位置,分别写出边长为2的正方形ABCD的各点坐标.
解:(1)A(0,0),B(-2,0),C(-2,2),D(0,2);
(2)A(0,0),B(-2,0),C(-2,-2),D(0,-2);
(3)A(0,0),B(0,-2),C(2,-2),D(2,0).
平面直角坐标系及点的坐标
定义:原点、坐标轴
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
课堂小结
1.教材P69~70习题7.1第2,3,4,5,6题;
2.完成对应课时练习.
作业布置
