7.2.1 用坐标表示地理位置 课件(共22张PPT)
文档属性
| 名称 | 7.2.1 用坐标表示地理位置 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-22 17:34:33 | ||
图片预览








文档简介
(共22张PPT)
第七章 平面直角坐标系
7.1 平面直角坐标系
7.2.1 用坐标表示地理位置
学习目标
1.了解通过平面直角坐标系来表示地理位置的意义及主要过程.
2.能用坐标来描述地理位置.
3.知道方位角和距离也可以表示平面内物体的位置.
重点:利用坐标表示地理位置.
难点:建立适当的坐标系,利用平面直角坐标系解决实际问题.
课前预习
阅读课本第P72-75页内容,学习本节主要内容.
单位长度
原点
正方向
坐标
名称
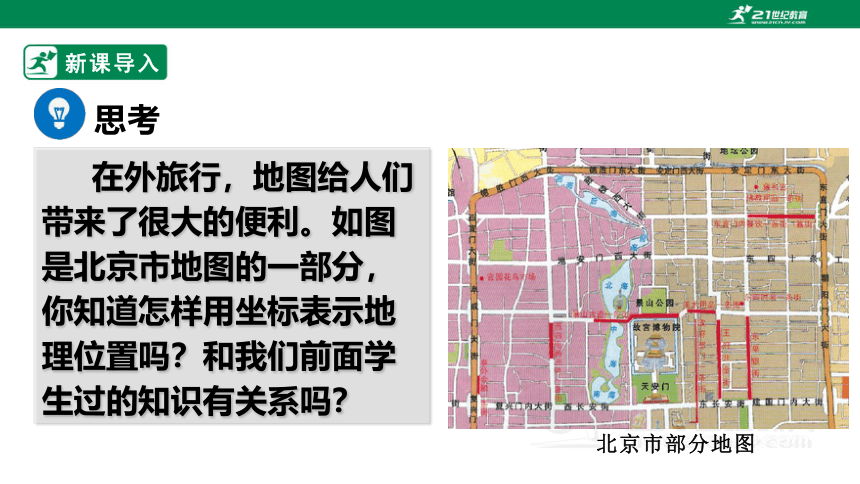
在外旅行,地图给人们带来了很大的便利。如图是北京市地图的一部分,你知道怎样用坐标表示地理位置吗?和我们前面学生过的知识有关系吗?
北京市部分地图
思考
新课导入
根据以下条件画一幅示意图,你能指出学校和小刚家,小强家,小敏家的位置吗?
小刚家:出校门向东走 1 500 m,再向北
走 2 000 m.
探究
小刚家
小强家
小敏家
校门
北
小强家:出校门向西走 2 000 m,再向北
走 3 500 m,最后向东走 500 m.
小敏家:出校门向南走 1 000 m,再向东
走 3 000 m,最后向南走 750 m.
探究新知
解:以学校为坐标原点,分别以正东、正北方向为x轴、y轴正方向建立直角坐标系,规定一个单位长度代表500m长.
问题1 如何建立平面直角坐标系呢?以何参照点为原点?如何确定x轴、y轴?如何确定单位长度?
校门
x
y
小刚家
( 1500 , 2000)
小强家
( -1500 , 3500)
小敏家
( 3000 , -1750 )
你能标明它们各个家的坐标吗?
500
问题2 选取学校所在位置为原点,并以正东,正北方向为 x 轴、y 轴的正方向有什么优点?
解:选取学校所在位置为原点,并以正东,正北方向为 x 轴,y 轴正方向,可以容易地写出三位同学家的位置的坐标.
x
y
校门
利用平面直角坐标系描述地理位置时应注意哪些问题?
要标明比例尺或坐标轴上的单位长度;
选择的坐标原点不同,建立的坐标系就不同,得到的点的坐标也就不同,但它们的相对位置始终不变.
思考
01
02
利用平面直角坐标系表示地理位置的步骤:
最关键一步!
(1)建立平面直角坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴及其正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
知识归纳
思考
如图,一艘船在 A 处遇险后向相距 35 n mile 位于 B 处的救生船报警,如何用方向和距离描述救生船相对于遇险船的位置?
救生船接到报警后准备前往救援,如何用方向和距离描述遇险船相对于救生船的位置?
探究新知
由图可知:
5nmile
(1)救生船在遇险船北偏东60°的方向上,与遇险船的距离是35n mile,北偏东60°, 35n mile就可以确定救生船相对于遇险船的位置.
(2)反过来,用南偏西60°, 35n mile就可以确定遇险船相对于救生船的位置.
如何用方位角和距离表示平面内物体的位置?
(1)找到参照点;
思考
(2)在该点建立方向标;
(3)根据方位角和距离表示出平面内的点.
利用“方位角+距离”描述地理位置时应注意哪些问题?
(1)用方位角和距离表示平面内点的位置时,必须要有两个数据:
思考
(2)方位角的表示方法具有规定性,以正北或正南方向为基准,以向东或向西偏离的角度表示方位角,共有四种形式:
①该点相对于参照点的方位;
北偏东 x°
北偏西 x°
南偏东 x°
南偏西 x°
②该点与参照点之间的实际距离;
1. 长方形零件如图(单位:mm),建立适当的坐标系,用坐标表示孔心的位置.
解:如图所示.
孔心的位置为(0,25)
随堂练习
2. 如图,货轮与灯塔相距 40 n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
解:灯塔在货轮南偏东50°方向,且相距40n mile;
货轮在灯塔北偏西50°方向,且相距40n mile.
例1 中国象棋棋盘中隐藏着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图中“马”所在的位置可以直接走到B,A等处.
(1)若“马”的位置在点C,为了到达点D,请按“马”走的规则,在图中用虚线画出一种你认为合理的行走路线;
(2)如果图中“马”位于(1,-2)上,试写出A,B,C,D四点的坐标.
解:(1)如图所示;
(2)建立如图所示的坐标系,
楚河 汉界
B
A
C
D
A(3,-1),B(2,0),C(6,2),D(7,-1).
例题分析
例2 如图是某次海战中敌我双方舰艇对峙示意图,对我方潜艇来说:
(1)北偏东40°的方向上有哪些目标?要想确定敌方战舰B的位置,还需要什么数据?
(2)距我方潜艇图上距离约为1cm处的敌舰有哪几艘?
(3)要确定每艘敌舰的位置,各需要几个数据?
解:(1)有敌方战舰B和小岛,还需知道敌方战舰B距我方潜艇的距离;
(2)有敌方战舰A和敌方战舰C;
(3)各需2个数据:方位角和距离.
3.如图是某市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )
A.(2,1) B.(0,1)
C.(-2,-1) D.(-2,1)
C
随堂练习
(1)图中距小明家距离相同的是哪些地方?
(2)商场B、学校A、公园C、停车场P分别在小明家的什么方向?
解:(1)图中距小明家距离相同的是学校与公园;
4.如图是小明家O和学校A所在地的简单地图.已知OA=2 cm,OB=2.5 cm,OP=4 cm,C为OP的中点.
(2)商场B在小明家的北偏西30°方向;
学校A在小明家的东北方向;
公园C、停车场P在小明家的南偏东60°方向;
(3)如果学校距离小明家400 m,那么商场和停车场分别距离小明家多少米?
解:学校距离小明家400 m,而OA=2 cm,
故比例尺为1∶20 000.
故商场距离小明家2.5×20 000÷100=500(m);
停车场距离小明家4×20 000÷100=800(m).
用平面直角坐标系表示地理位置
用方位角和距离表示平面内物体的位置
建立坐标系
确定单位长度
画点并写出各点的坐标及各个地点的名称
用坐标表示地理位置
课堂总结
1.教材P78~79习题7.2第1,2,5,6题;
2.完成对应课时练习.
作业布置
第七章 平面直角坐标系
7.1 平面直角坐标系
7.2.1 用坐标表示地理位置
学习目标
1.了解通过平面直角坐标系来表示地理位置的意义及主要过程.
2.能用坐标来描述地理位置.
3.知道方位角和距离也可以表示平面内物体的位置.
重点:利用坐标表示地理位置.
难点:建立适当的坐标系,利用平面直角坐标系解决实际问题.
课前预习
阅读课本第P72-75页内容,学习本节主要内容.
单位长度
原点
正方向
坐标
名称
在外旅行,地图给人们带来了很大的便利。如图是北京市地图的一部分,你知道怎样用坐标表示地理位置吗?和我们前面学生过的知识有关系吗?
北京市部分地图
思考
新课导入
根据以下条件画一幅示意图,你能指出学校和小刚家,小强家,小敏家的位置吗?
小刚家:出校门向东走 1 500 m,再向北
走 2 000 m.
探究
小刚家
小强家
小敏家
校门
北
小强家:出校门向西走 2 000 m,再向北
走 3 500 m,最后向东走 500 m.
小敏家:出校门向南走 1 000 m,再向东
走 3 000 m,最后向南走 750 m.
探究新知
解:以学校为坐标原点,分别以正东、正北方向为x轴、y轴正方向建立直角坐标系,规定一个单位长度代表500m长.
问题1 如何建立平面直角坐标系呢?以何参照点为原点?如何确定x轴、y轴?如何确定单位长度?
校门
x
y
小刚家
( 1500 , 2000)
小强家
( -1500 , 3500)
小敏家
( 3000 , -1750 )
你能标明它们各个家的坐标吗?
500
问题2 选取学校所在位置为原点,并以正东,正北方向为 x 轴、y 轴的正方向有什么优点?
解:选取学校所在位置为原点,并以正东,正北方向为 x 轴,y 轴正方向,可以容易地写出三位同学家的位置的坐标.
x
y
校门
利用平面直角坐标系描述地理位置时应注意哪些问题?
要标明比例尺或坐标轴上的单位长度;
选择的坐标原点不同,建立的坐标系就不同,得到的点的坐标也就不同,但它们的相对位置始终不变.
思考
01
02
利用平面直角坐标系表示地理位置的步骤:
最关键一步!
(1)建立平面直角坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴及其正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
知识归纳
思考
如图,一艘船在 A 处遇险后向相距 35 n mile 位于 B 处的救生船报警,如何用方向和距离描述救生船相对于遇险船的位置?
救生船接到报警后准备前往救援,如何用方向和距离描述遇险船相对于救生船的位置?
探究新知
由图可知:
5nmile
(1)救生船在遇险船北偏东60°的方向上,与遇险船的距离是35n mile,北偏东60°, 35n mile就可以确定救生船相对于遇险船的位置.
(2)反过来,用南偏西60°, 35n mile就可以确定遇险船相对于救生船的位置.
如何用方位角和距离表示平面内物体的位置?
(1)找到参照点;
思考
(2)在该点建立方向标;
(3)根据方位角和距离表示出平面内的点.
利用“方位角+距离”描述地理位置时应注意哪些问题?
(1)用方位角和距离表示平面内点的位置时,必须要有两个数据:
思考
(2)方位角的表示方法具有规定性,以正北或正南方向为基准,以向东或向西偏离的角度表示方位角,共有四种形式:
①该点相对于参照点的方位;
北偏东 x°
北偏西 x°
南偏东 x°
南偏西 x°
②该点与参照点之间的实际距离;
1. 长方形零件如图(单位:mm),建立适当的坐标系,用坐标表示孔心的位置.
解:如图所示.
孔心的位置为(0,25)
随堂练习
2. 如图,货轮与灯塔相距 40 n mile,如何用方向和距离描述灯塔相对于货轮的位置?反过来,如何用方向和距离描述货轮相对于灯塔的位置?
解:灯塔在货轮南偏东50°方向,且相距40n mile;
货轮在灯塔北偏西50°方向,且相距40n mile.
例1 中国象棋棋盘中隐藏着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图中“马”所在的位置可以直接走到B,A等处.
(1)若“马”的位置在点C,为了到达点D,请按“马”走的规则,在图中用虚线画出一种你认为合理的行走路线;
(2)如果图中“马”位于(1,-2)上,试写出A,B,C,D四点的坐标.
解:(1)如图所示;
(2)建立如图所示的坐标系,
楚河 汉界
B
A
C
D
A(3,-1),B(2,0),C(6,2),D(7,-1).
例题分析
例2 如图是某次海战中敌我双方舰艇对峙示意图,对我方潜艇来说:
(1)北偏东40°的方向上有哪些目标?要想确定敌方战舰B的位置,还需要什么数据?
(2)距我方潜艇图上距离约为1cm处的敌舰有哪几艘?
(3)要确定每艘敌舰的位置,各需要几个数据?
解:(1)有敌方战舰B和小岛,还需知道敌方战舰B距我方潜艇的距离;
(2)有敌方战舰A和敌方战舰C;
(3)各需2个数据:方位角和距离.
3.如图是某市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )
A.(2,1) B.(0,1)
C.(-2,-1) D.(-2,1)
C
随堂练习
(1)图中距小明家距离相同的是哪些地方?
(2)商场B、学校A、公园C、停车场P分别在小明家的什么方向?
解:(1)图中距小明家距离相同的是学校与公园;
4.如图是小明家O和学校A所在地的简单地图.已知OA=2 cm,OB=2.5 cm,OP=4 cm,C为OP的中点.
(2)商场B在小明家的北偏西30°方向;
学校A在小明家的东北方向;
公园C、停车场P在小明家的南偏东60°方向;
(3)如果学校距离小明家400 m,那么商场和停车场分别距离小明家多少米?
解:学校距离小明家400 m,而OA=2 cm,
故比例尺为1∶20 000.
故商场距离小明家2.5×20 000÷100=500(m);
停车场距离小明家4×20 000÷100=800(m).
用平面直角坐标系表示地理位置
用方位角和距离表示平面内物体的位置
建立坐标系
确定单位长度
画点并写出各点的坐标及各个地点的名称
用坐标表示地理位置
课堂总结
1.教材P78~79习题7.2第1,2,5,6题;
2.完成对应课时练习.
作业布置
