人教版九年级下学期试数学开学测试B卷(附答案解析)
文档属性
| 名称 | 人教版九年级下学期试数学开学测试B卷(附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 13:42:11 | ||
图片预览



文档简介
人教版九年级下学期数学开学测试
B卷
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.某城市市区人口x万人,市区绿地面积50万平方米,平均每人拥有绿地y平方米,则y与x之间的函数表达式为( )
A. B. C. D.
2.在“双减政策”的推动下,某校学生课后作业时长有了明显的减少.去年上半年平均每周作业时长为a分钟,经过去年下半年和今年上半年两次整改后,现在平均每周作业时长比去年上半年减少了70%,设每半年平均每周作业时长的下降率为x,则可列方程为( )
A. B.
C. D.
3.下列说法正确的是( )
A.自然现象中,“太阳东方升起”是必然事件
B.成语“水中捞月”所描述的事件,是随机事件
C.“襄阳明天降雨的概率为0.6”,表示襄阳明天一定降雨
D.若抽奖活动的中奖概率为,则抽奖50次必中奖1次
4.在平面直角坐标系中,以原点为对称中心,把点逆时针旋转90°,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3) C.(-3,4) D.(-3,-4)
5.如图,AB为的直径,PD是的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若,,则BD的长为( )
A. B. C. D.
6.已知实数x满足,则的值是( )
A.-2 B.-2或6 C.6 D.604
7.某校开展岗位体验劳动教育活动,设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位,每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动,则这两名同学恰好在同一岗位体验的概率为( )
A. B. C. D.
8.如图,已知中,,,将绕A点逆时针旋转50°得到,以下结论:①,②,③,④,正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
9.如图,在矩形ABCD中,,,,,则四边形EFGH面积的最大值是( )
A. B. C. D.
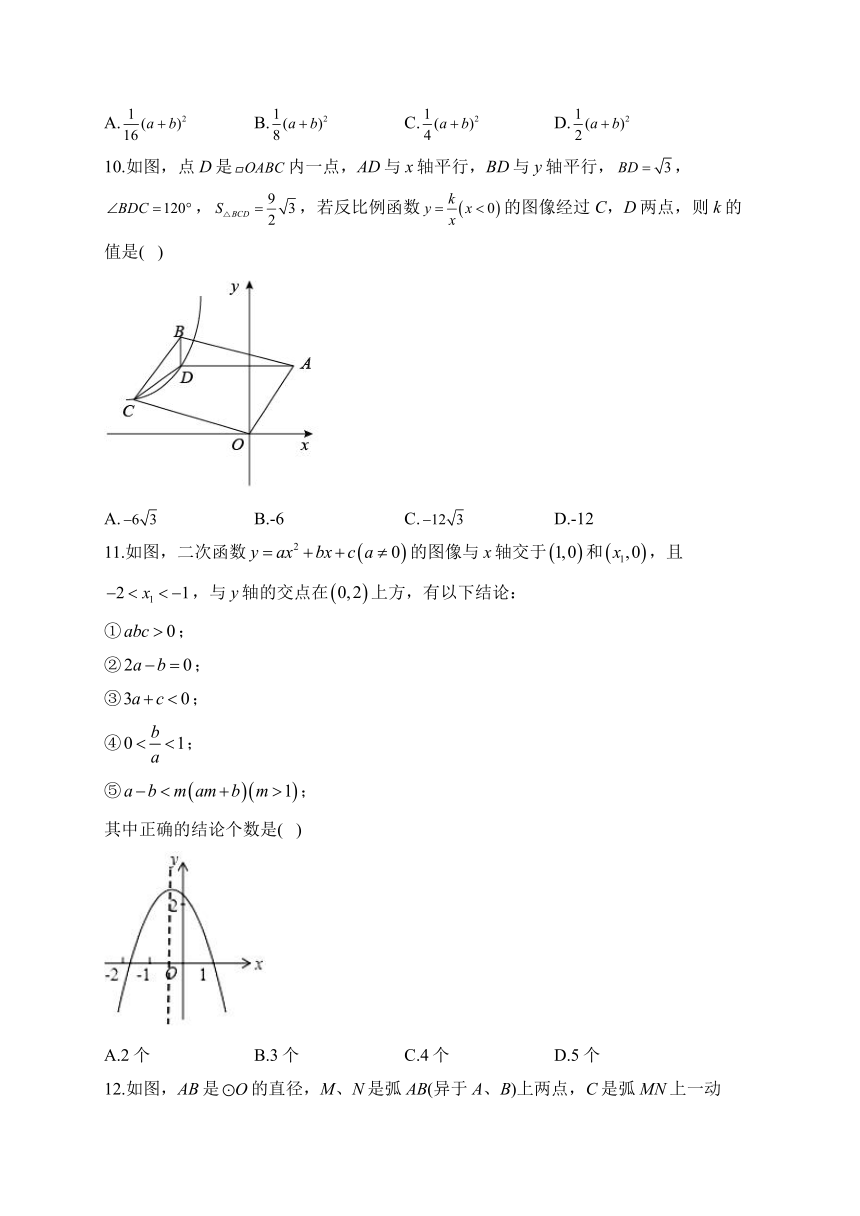
10.如图,点D是内一点,AD与x轴平行,BD与y轴平行,,,,若反比例函数的图像经过C,D两点,则k的值是( )
A. B.-6 C. D.-12
11.如图,二次函数的图像与x轴交于和,且,与y轴的交点在上方,有以下结论:
①;
②;
③;
④;
⑤;
其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
12.如图,AB是的直径,M、N是弧AB(异于A、B)上两点,C是弧MN上一动点,的角平分线交于点D,的平分线交CD于点E.当点C从点M运动到点N时,则C、E两点的运动路径长的比是( )
A. B. C. D.
二、填空题:(每小题3分,共18分)
13.经过某十字路口的汽车,它可能直行,也可能向左转或向右转,假设这三种可能性大小相同,那么两辆汽车经过这个十字路口,一辆向左转,一辆向右转的概率是_____.
14.如图,在等腰中,,,将绕着点A按顺时针方向旋转90°得到,连接,若,则五边形的面积是___________.
15.已知二次函数图象上三点,,则,,的大小关系为__________.
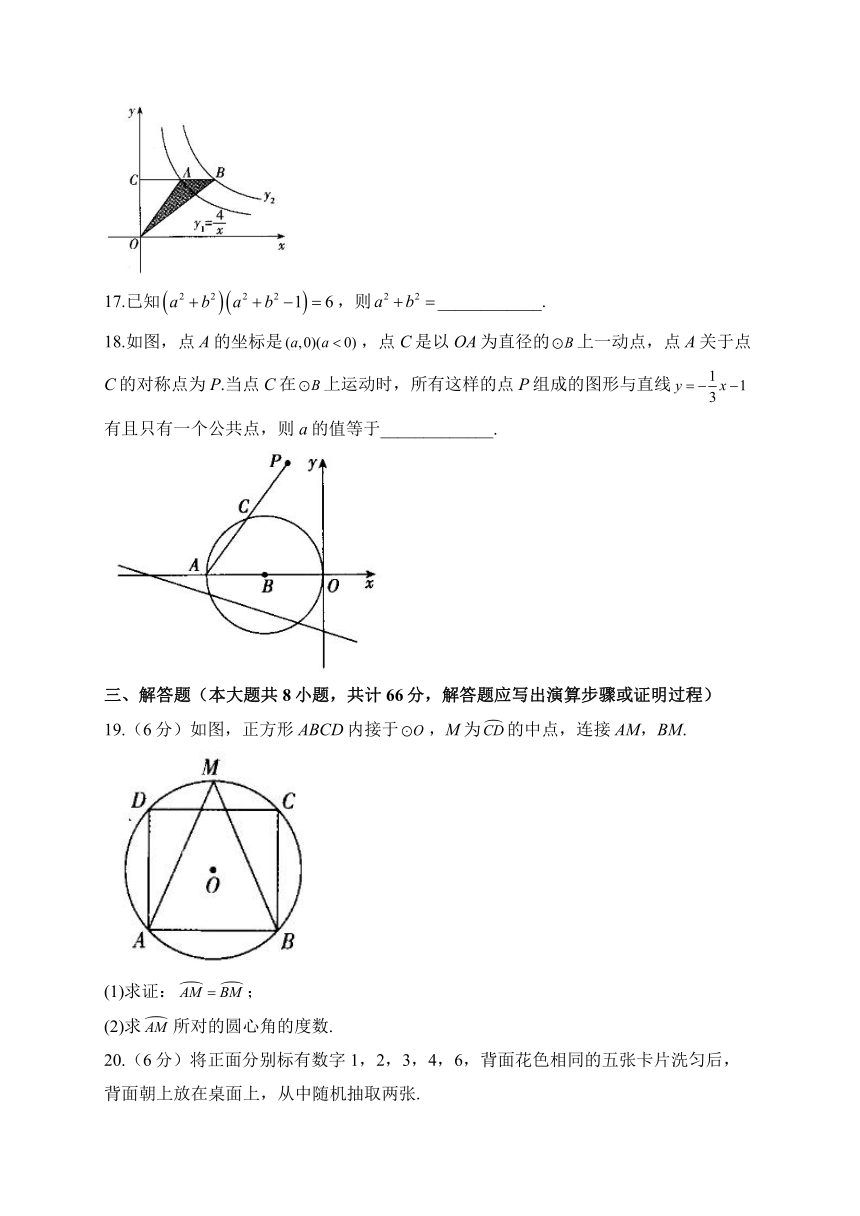
16.反比例函数,在第一象限的图象如图,已知,过的图象上的任意一点A作x轴的平行线交的图象于点B,交y轴于点C,若,则的表达式是___________.
17.已知,则____________.
18.如图,点A的坐标是,点C是以OA为直径的上一动点,点A关于点C的对称点为P.当点C在上运动时,所有这样的点P组成的图形与直线有且只有一个公共点,则a的值等于_____________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,正方形ABCD内接于,M为的中点,连接AM,BM.
(1)求证:;
(2)求所对的圆心角的度数.
20.(6分)将正面分别标有数字1,2,3,4,6,背面花色相同的五张卡片洗匀后,背面朝上放在桌面上,从中随机抽取两张.
(1)写出所有机会均等的结果,并求抽出的两张卡片上的数字之和为偶数的概率;
(2)记抽得的两张卡片的数字为,求点在直线上的概率.
21.(8分)二次函数图象的对称轴在y轴的右侧.
(1)当时,直接写出二次函数图象的顶点坐标;
(2)探究该二次函数的图象是否过定点;
(3)若点在该二次函数的图象上,且.若过点作x轴垂线,与二次函数的交点在x轴的上方,求m的取值范围.
22.(8分)如图,已知一次函数与反比例函数的图象交于,两点,且与x轴和y轴分别交于点C、点D.
(1)根据图象直接写出不等式的解集;
(2)求反比例函数与一次函数的解析式;
(3)点P在y轴上,且,请求出点P的坐标.
23.(8分)如图,的直径AB垂直于弦DC于点F,点P在AB的延长线上,CP与相切于点C.
(1)求证:;
(2)若的直径为4,弦DC平分半径OB,求:图中阴影部分的面积.
24.(8分)某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件,第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)图中点P所表示的实际意义是________;销售单价每提高1元时,销售量相应减少_________件;
(2)请直接写出y与x之间的函数表达式:__________;自变量x的取值范围为__________;
(3)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
25.(10分)已知,是一元二次方程的两个实数根.
(1)求m的取值范围;
(2)是否存在实数m,使得等式成立?如果存在,请求出m的值;如果不存在,请说明理由.
26.(12分)如图1,已知直线l垂直线段AB于点B,点P是直线l上异于点B的一个动点,线段AP绕点P顺时针旋转得到线段CP,线段BP绕点P逆时针旋转得到线段DP,连结AC,BD,CD,CD与直线l交于点E,.
(1)如图2(点P在点B上方时),过点C作直线l的垂线,垂足为F.
①求证:.
②求PE的长.
(2)在点P的运动过程中,点P,E,B三点中,是否存在其中一点恰是另外两点为端点的线段的中点,若存在,求出相应CD的长,若不存在,说明相应理由.
答案以及解析
1.答案:C
解析:由城市市区人口x万人,市区绿地面积50万平方米,则平均每人拥有绿地.故选:C.
2.答案:C
解析:设每半年平均每周作业时长的下降率为x,
去年上半年平均每周作业时长为a分钟,
去年下半年平均每周作业时长为分钟,
今年上半年平均每周作业时长为分钟,
现在平均每周作业时长比去年上半年减少了,
,
.
故选:C.
3.答案:A
解析:A、自然现象中,“太阳东方升起”是必然事件,故A符合题意;
B、成语“水中捞月”所描述的事件,是不可能事件,故B不符合题意;
C、襄阳明天降雨的概率为0.6”,表示襄阳明天降雨的可能性是60%,故C不符合题意;
D、若抽奖活动的中奖概率为,则抽奖50次不50一定中奖1次,故D不符合题意;
故选:A.
4.答案:B
解析:如图,由旋转的性质,得,,
点B在第二象限,.
5.答案:A
解析:连接CO.是的切线,点C为切点,.,,.,,,,.
6.答案:C
解析:设,则方程变形为:
,
即,
或6,即或6;
当时,此方程无实数根(舍),
当时,满足题意.
故选:C.
7.答案:A
解析:本题考查用列表法或画树状图法求概率.根据题意画树状图如图所示,由树状图可知,共有16种等可能的情况,其中甲、乙两名同学恰好在同一岗位体验的情况共有4种,这两名同学恰好在同一岗位体验的概率为,故选A.
8.答案:B
解析:①绕A点逆时针旋转50°得到,.故①正确;②绕A点逆时针旋转50°,.,.,.,.故②正确;③在中,,,..与不垂直.故③不正确;④在中,,,..故④正确.①②④这三个结论正确.故选:B.
9.答案:B
解析:设,则,.设四边形EFGH的面积为y,依题意,得,即.,抛物线开口向下,时,y有最大值.由题意知,,函数最大值为.故选B.
10.答案:C
解析:过点C作轴,延长BD交CE于点F,
四边形OABC为平行四边形,
,,
,
BD与y轴平行,
,
在和中,
,
,
,
,
,
,
,
,
点D的纵坐标为,
设,则,
反比例函数的图象经过C,D两点,
,,,
故选:C.
11.答案:A
解析:由图象可知,对称轴为,故,与y轴的交点在正半轴,故,故,①正确;
有图象可知,得,即,②错误;
由,得,故④错误;
设函数与x轴的交点的横坐标为,,则可知,,
,即,,,③正确;
对于,,
则,
,故开口向下,不可能恒大于0,⑤错误;
综上所述,①③正确,
故选:A.
12.答案:A
解析:连结BE,
点E是与的交点,
点E是的内心,
BE平分,
AB为直径,
,
,为定值,,
点E的轨迹是弓形AB上的圆弧,
此圆弧的圆心一定在弦AB的中垂线上,
,
,
如下图,过圆心O作直径CD,则,
,
在CD的延长线上,作,
则,
即,
A、E、B、F四点共圆,
,
,
点D为弓形AB所在圆的圆心,
设的半径为R,
则点C的运动路径长为:,
,
点E的运动路径为弧AEB,弧长为:,
C、E两点的运动路径长比为:,
故选A.
13.答案:
解析:画“树形图”列举这两辆汽车行驶方向所有可能的结果如图所示:
这两辆汽车行驶方向共有9种可能的结果,两辆汽车一辆左转,一辆右转的结果有2种,且所有结果的可能性相等,
,
故答案为:.
14.答案:5
解析:如图:过点C作于点D,
,
,
,
将绕着点A按顺时针方向旋转得到,
,,,
,
,
四边形是矩形,
,,
,
故答案为:5.
15.答案:
解析:二次函数中,,
函数图象开口向下,对称轴是直线,
关于直线的对称点是,当时,y随x的增大而减小,
,
,
故答案为:.
16.答案:
解析:设的表达式为,轴,,,,,,的表达式为.
17.答案:3
解析:设,
则原方程化为:,
去括号移项得:,
,
解得,,
,
.
故答案为:3.
18.答案:
解析:如图,连接BC,OP.设直线交x轴于点,交y轴于点.,,,点P的运动轨迹是以O为圆心,为半径的圆,当与直线相切时,点P组成的图形与直线有且只有一个公共点,设切点为G,连接OG.在中,,,,,,故答案为.
19.答案:(1)见解析
(2)所对的圆心角的度数是135°
解析:(1)四边形ABCD是正方形,,.
为的中点,,
,
.
(2)连接OM,OA,OB,正方形ABCD内接于,,,.,,,,,所对的圆心角的度数是135°.
20.答案:(1)
(2)
解析:(1)列表得:
-
-
-
-
-
共有20种等可能的结果,抽出的两张卡片上的数字之和为偶数的有8种情况.
故所求概率为;
(2)抽得的两个数字分别作为点P横、纵坐标共有20种机会均等的结果,在直线上的只有,,三种情况,故所求概率.
21.答案:(1)
(2)过定点
(3)
解析:(1)若,则,
顶点坐标为
(2)过定点.
证明:
过定点
(3)二次函数图象与x轴的交点为,
点在该二次函数的图象上,且
由不等式的性质可得,
又二次函数图象的对称轴在y轴的右侧,
直线与二次函数图象的交点在x轴的上方,
,
.
22.答案:(1)
(2)
(3)或
解析:(1)当的图象在图象的下方时,成立,
.
(2)将代入得:,
反比例函数为:.
将,代入得:,
解得:,
一次函数的表达式为:.
(3)在中,当时,,
.
,
,
P在y轴上,
,
.
或.
23.答案:(1)见解析
(2)
解析:(1)证明:如图,连接OC,
CP与相切,
,
,
,
,
,
由圆周角定理得:,
(2)连接OD,
在中,,
则,
,
,
,
,
,
.
24.答案:(1)当售价定为35元/件时销售量为300件;20;
(2),;
(3)第二个月的销售单价定为35元时,可获得最大利润,最大利润是4500元.
解析:(1)图中点P所表示的实际意义是:当售价定为35元/件时,销售数量为300件;
第一个月的该商品的售价为:(元),
销售单价每提高1元时,销售量相应减少数量为:(件).
故答案为当售价定为35元/件时,销售数量为300件;20.
(2)设y与x之间的函数表达式为,
将点、代入中,
得:,
解得,
y与x之间的函数表达式为.
当时,,
自变量x的取值范围为.
故答案为;.
(3)设第二个月的利润为w元,
由已知得:,
,
当时,w取最大值,最大值为4500.
故第二个月的销售单价定为35元时,可获得最大利润,最大利润是4500元.
25.答案:(1)
(2)存在m的值为,使得等式成立
解析:(1)一元二次方程有两个实数根,
,
解得.
(2)存在实数m.
是一元二次方程的两个实数根,
,
,
,
解得,
又,
.
存在m的值为,使得等式成立.
26.答案:(1)①见详解;②2
(2)存在,或或
解析:(1)①由旋转的性质可得:,,,,
,
,,
,,
,
,
②,
,,
,
,
又,,
,
.
(2)存在,理由如下:
如图,①当P为BE的中点时,
结合(1)可得:,
,
,
那么此时.
②当B为PE的中点时,如图
同理可得:,
,,
同理可得:,
,,,
那么,
③当E为PB的中点时,如图,
同理可得:,
,,
同理可得:,
,,
B,F两点重合,
,
,
.
综上:CD的长度为:或或.
B卷
【满分:120分】
一、选择题:(本大题共12小题,每小题3分,共36分,给出的四个选项中,只有一项是符合题目要求的)
1.某城市市区人口x万人,市区绿地面积50万平方米,平均每人拥有绿地y平方米,则y与x之间的函数表达式为( )
A. B. C. D.
2.在“双减政策”的推动下,某校学生课后作业时长有了明显的减少.去年上半年平均每周作业时长为a分钟,经过去年下半年和今年上半年两次整改后,现在平均每周作业时长比去年上半年减少了70%,设每半年平均每周作业时长的下降率为x,则可列方程为( )
A. B.
C. D.
3.下列说法正确的是( )
A.自然现象中,“太阳东方升起”是必然事件
B.成语“水中捞月”所描述的事件,是随机事件
C.“襄阳明天降雨的概率为0.6”,表示襄阳明天一定降雨
D.若抽奖活动的中奖概率为,则抽奖50次必中奖1次
4.在平面直角坐标系中,以原点为对称中心,把点逆时针旋转90°,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3) C.(-3,4) D.(-3,-4)
5.如图,AB为的直径,PD是的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若,,则BD的长为( )
A. B. C. D.
6.已知实数x满足,则的值是( )
A.-2 B.-2或6 C.6 D.604
7.某校开展岗位体验劳动教育活动,设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位,每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动,则这两名同学恰好在同一岗位体验的概率为( )
A. B. C. D.
8.如图,已知中,,,将绕A点逆时针旋转50°得到,以下结论:①,②,③,④,正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
9.如图,在矩形ABCD中,,,,,则四边形EFGH面积的最大值是( )
A. B. C. D.
10.如图,点D是内一点,AD与x轴平行,BD与y轴平行,,,,若反比例函数的图像经过C,D两点,则k的值是( )
A. B.-6 C. D.-12
11.如图,二次函数的图像与x轴交于和,且,与y轴的交点在上方,有以下结论:
①;
②;
③;
④;
⑤;
其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
12.如图,AB是的直径,M、N是弧AB(异于A、B)上两点,C是弧MN上一动点,的角平分线交于点D,的平分线交CD于点E.当点C从点M运动到点N时,则C、E两点的运动路径长的比是( )
A. B. C. D.
二、填空题:(每小题3分,共18分)
13.经过某十字路口的汽车,它可能直行,也可能向左转或向右转,假设这三种可能性大小相同,那么两辆汽车经过这个十字路口,一辆向左转,一辆向右转的概率是_____.
14.如图,在等腰中,,,将绕着点A按顺时针方向旋转90°得到,连接,若,则五边形的面积是___________.
15.已知二次函数图象上三点,,则,,的大小关系为__________.
16.反比例函数,在第一象限的图象如图,已知,过的图象上的任意一点A作x轴的平行线交的图象于点B,交y轴于点C,若,则的表达式是___________.
17.已知,则____________.
18.如图,点A的坐标是,点C是以OA为直径的上一动点,点A关于点C的对称点为P.当点C在上运动时,所有这样的点P组成的图形与直线有且只有一个公共点,则a的值等于_____________.
三、解答题(本大题共8小题,共计66分,解答题应写出演算步骤或证明过程)
19.(6分)如图,正方形ABCD内接于,M为的中点,连接AM,BM.
(1)求证:;
(2)求所对的圆心角的度数.
20.(6分)将正面分别标有数字1,2,3,4,6,背面花色相同的五张卡片洗匀后,背面朝上放在桌面上,从中随机抽取两张.
(1)写出所有机会均等的结果,并求抽出的两张卡片上的数字之和为偶数的概率;
(2)记抽得的两张卡片的数字为,求点在直线上的概率.
21.(8分)二次函数图象的对称轴在y轴的右侧.
(1)当时,直接写出二次函数图象的顶点坐标;
(2)探究该二次函数的图象是否过定点;
(3)若点在该二次函数的图象上,且.若过点作x轴垂线,与二次函数的交点在x轴的上方,求m的取值范围.
22.(8分)如图,已知一次函数与反比例函数的图象交于,两点,且与x轴和y轴分别交于点C、点D.
(1)根据图象直接写出不等式的解集;
(2)求反比例函数与一次函数的解析式;
(3)点P在y轴上,且,请求出点P的坐标.
23.(8分)如图,的直径AB垂直于弦DC于点F,点P在AB的延长线上,CP与相切于点C.
(1)求证:;
(2)若的直径为4,弦DC平分半径OB,求:图中阴影部分的面积.
24.(8分)某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件,第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)图中点P所表示的实际意义是________;销售单价每提高1元时,销售量相应减少_________件;
(2)请直接写出y与x之间的函数表达式:__________;自变量x的取值范围为__________;
(3)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
25.(10分)已知,是一元二次方程的两个实数根.
(1)求m的取值范围;
(2)是否存在实数m,使得等式成立?如果存在,请求出m的值;如果不存在,请说明理由.
26.(12分)如图1,已知直线l垂直线段AB于点B,点P是直线l上异于点B的一个动点,线段AP绕点P顺时针旋转得到线段CP,线段BP绕点P逆时针旋转得到线段DP,连结AC,BD,CD,CD与直线l交于点E,.
(1)如图2(点P在点B上方时),过点C作直线l的垂线,垂足为F.
①求证:.
②求PE的长.
(2)在点P的运动过程中,点P,E,B三点中,是否存在其中一点恰是另外两点为端点的线段的中点,若存在,求出相应CD的长,若不存在,说明相应理由.
答案以及解析
1.答案:C
解析:由城市市区人口x万人,市区绿地面积50万平方米,则平均每人拥有绿地.故选:C.
2.答案:C
解析:设每半年平均每周作业时长的下降率为x,
去年上半年平均每周作业时长为a分钟,
去年下半年平均每周作业时长为分钟,
今年上半年平均每周作业时长为分钟,
现在平均每周作业时长比去年上半年减少了,
,
.
故选:C.
3.答案:A
解析:A、自然现象中,“太阳东方升起”是必然事件,故A符合题意;
B、成语“水中捞月”所描述的事件,是不可能事件,故B不符合题意;
C、襄阳明天降雨的概率为0.6”,表示襄阳明天降雨的可能性是60%,故C不符合题意;
D、若抽奖活动的中奖概率为,则抽奖50次不50一定中奖1次,故D不符合题意;
故选:A.
4.答案:B
解析:如图,由旋转的性质,得,,
点B在第二象限,.
5.答案:A
解析:连接CO.是的切线,点C为切点,.,,.,,,,.
6.答案:C
解析:设,则方程变形为:
,
即,
或6,即或6;
当时,此方程无实数根(舍),
当时,满足题意.
故选:C.
7.答案:A
解析:本题考查用列表法或画树状图法求概率.根据题意画树状图如图所示,由树状图可知,共有16种等可能的情况,其中甲、乙两名同学恰好在同一岗位体验的情况共有4种,这两名同学恰好在同一岗位体验的概率为,故选A.
8.答案:B
解析:①绕A点逆时针旋转50°得到,.故①正确;②绕A点逆时针旋转50°,.,.,.,.故②正确;③在中,,,..与不垂直.故③不正确;④在中,,,..故④正确.①②④这三个结论正确.故选:B.
9.答案:B
解析:设,则,.设四边形EFGH的面积为y,依题意,得,即.,抛物线开口向下,时,y有最大值.由题意知,,函数最大值为.故选B.
10.答案:C
解析:过点C作轴,延长BD交CE于点F,
四边形OABC为平行四边形,
,,
,
BD与y轴平行,
,
在和中,
,
,
,
,
,
,
,
,
点D的纵坐标为,
设,则,
反比例函数的图象经过C,D两点,
,,,
故选:C.
11.答案:A
解析:由图象可知,对称轴为,故,与y轴的交点在正半轴,故,故,①正确;
有图象可知,得,即,②错误;
由,得,故④错误;
设函数与x轴的交点的横坐标为,,则可知,,
,即,,,③正确;
对于,,
则,
,故开口向下,不可能恒大于0,⑤错误;
综上所述,①③正确,
故选:A.
12.答案:A
解析:连结BE,
点E是与的交点,
点E是的内心,
BE平分,
AB为直径,
,
,为定值,,
点E的轨迹是弓形AB上的圆弧,
此圆弧的圆心一定在弦AB的中垂线上,
,
,
如下图,过圆心O作直径CD,则,
,
在CD的延长线上,作,
则,
即,
A、E、B、F四点共圆,
,
,
点D为弓形AB所在圆的圆心,
设的半径为R,
则点C的运动路径长为:,
,
点E的运动路径为弧AEB,弧长为:,
C、E两点的运动路径长比为:,
故选A.
13.答案:
解析:画“树形图”列举这两辆汽车行驶方向所有可能的结果如图所示:
这两辆汽车行驶方向共有9种可能的结果,两辆汽车一辆左转,一辆右转的结果有2种,且所有结果的可能性相等,
,
故答案为:.
14.答案:5
解析:如图:过点C作于点D,
,
,
,
将绕着点A按顺时针方向旋转得到,
,,,
,
,
四边形是矩形,
,,
,
故答案为:5.
15.答案:
解析:二次函数中,,
函数图象开口向下,对称轴是直线,
关于直线的对称点是,当时,y随x的增大而减小,
,
,
故答案为:.
16.答案:
解析:设的表达式为,轴,,,,,,的表达式为.
17.答案:3
解析:设,
则原方程化为:,
去括号移项得:,
,
解得,,
,
.
故答案为:3.
18.答案:
解析:如图,连接BC,OP.设直线交x轴于点,交y轴于点.,,,点P的运动轨迹是以O为圆心,为半径的圆,当与直线相切时,点P组成的图形与直线有且只有一个公共点,设切点为G,连接OG.在中,,,,,,故答案为.
19.答案:(1)见解析
(2)所对的圆心角的度数是135°
解析:(1)四边形ABCD是正方形,,.
为的中点,,
,
.
(2)连接OM,OA,OB,正方形ABCD内接于,,,.,,,,,所对的圆心角的度数是135°.
20.答案:(1)
(2)
解析:(1)列表得:
-
-
-
-
-
共有20种等可能的结果,抽出的两张卡片上的数字之和为偶数的有8种情况.
故所求概率为;
(2)抽得的两个数字分别作为点P横、纵坐标共有20种机会均等的结果,在直线上的只有,,三种情况,故所求概率.
21.答案:(1)
(2)过定点
(3)
解析:(1)若,则,
顶点坐标为
(2)过定点.
证明:
过定点
(3)二次函数图象与x轴的交点为,
点在该二次函数的图象上,且
由不等式的性质可得,
又二次函数图象的对称轴在y轴的右侧,
直线与二次函数图象的交点在x轴的上方,
,
.
22.答案:(1)
(2)
(3)或
解析:(1)当的图象在图象的下方时,成立,
.
(2)将代入得:,
反比例函数为:.
将,代入得:,
解得:,
一次函数的表达式为:.
(3)在中,当时,,
.
,
,
P在y轴上,
,
.
或.
23.答案:(1)见解析
(2)
解析:(1)证明:如图,连接OC,
CP与相切,
,
,
,
,
,
由圆周角定理得:,
(2)连接OD,
在中,,
则,
,
,
,
,
,
.
24.答案:(1)当售价定为35元/件时销售量为300件;20;
(2),;
(3)第二个月的销售单价定为35元时,可获得最大利润,最大利润是4500元.
解析:(1)图中点P所表示的实际意义是:当售价定为35元/件时,销售数量为300件;
第一个月的该商品的售价为:(元),
销售单价每提高1元时,销售量相应减少数量为:(件).
故答案为当售价定为35元/件时,销售数量为300件;20.
(2)设y与x之间的函数表达式为,
将点、代入中,
得:,
解得,
y与x之间的函数表达式为.
当时,,
自变量x的取值范围为.
故答案为;.
(3)设第二个月的利润为w元,
由已知得:,
,
当时,w取最大值,最大值为4500.
故第二个月的销售单价定为35元时,可获得最大利润,最大利润是4500元.
25.答案:(1)
(2)存在m的值为,使得等式成立
解析:(1)一元二次方程有两个实数根,
,
解得.
(2)存在实数m.
是一元二次方程的两个实数根,
,
,
,
解得,
又,
.
存在m的值为,使得等式成立.
26.答案:(1)①见详解;②2
(2)存在,或或
解析:(1)①由旋转的性质可得:,,,,
,
,,
,,
,
,
②,
,,
,
,
又,,
,
.
(2)存在,理由如下:
如图,①当P为BE的中点时,
结合(1)可得:,
,
,
那么此时.
②当B为PE的中点时,如图
同理可得:,
,,
同理可得:,
,,,
那么,
③当E为PB的中点时,如图,
同理可得:,
,,
同理可得:,
,,
B,F两点重合,
,
,
.
综上:CD的长度为:或或.
同课章节目录
