2023年中考数学一轮复习学案:一元二次方程的运用(二)(无答案)
文档属性
| 名称 | 2023年中考数学一轮复习学案:一元二次方程的运用(二)(无答案) | 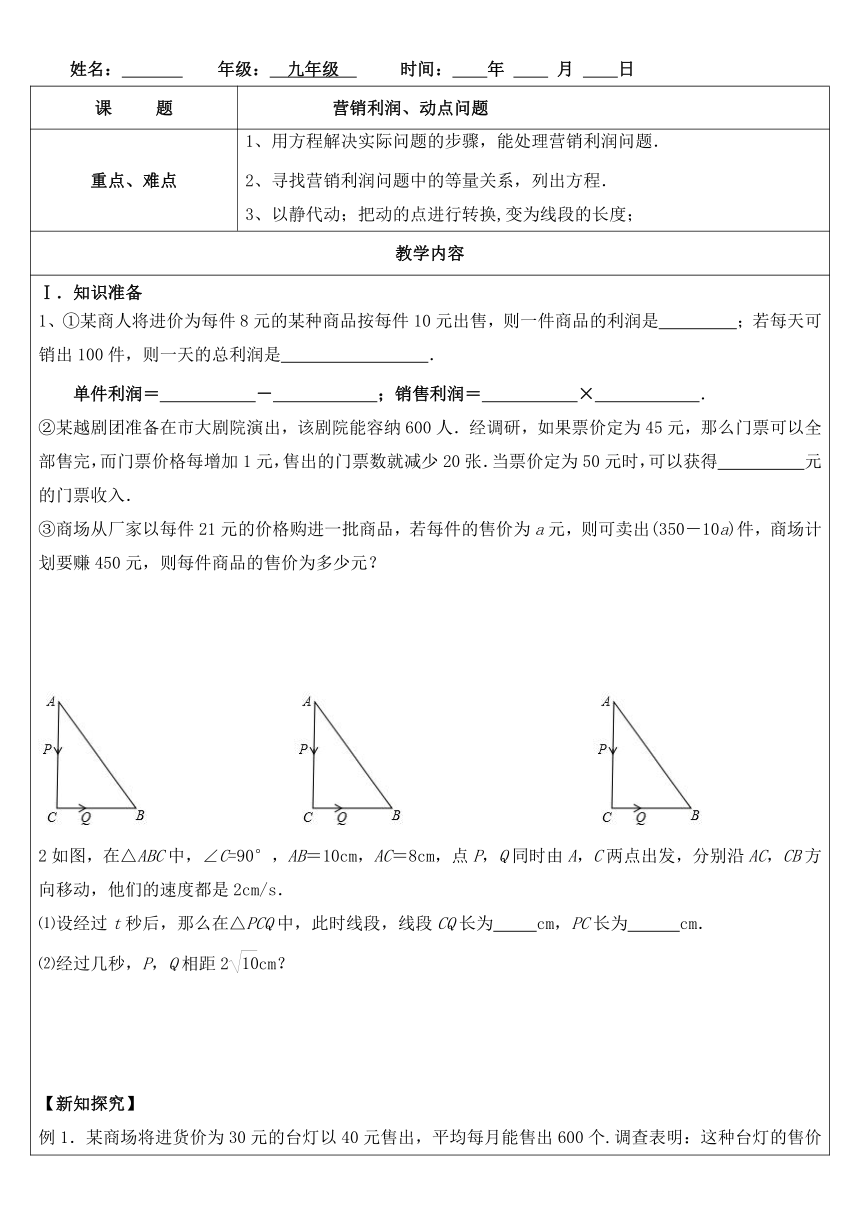 | |
| 格式 | docx | ||
| 文件大小 | 52.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 15:07:43 | ||
图片预览



文档简介
姓名: 年级: 九年级 时间: 年 月 日
课 题 营销利润、动点问题
重点、难点 1、用方程解决实际问题的步骤,能处理营销利润问题. 2、寻找营销利润问题中的等量关系,列出方程. 3、以静代动;把动的点进行转换,变为线段的长度;
教学内容
Ⅰ.知识准备 1、①某商人将进价为每件8元的某种商品按每件10元出售,则一件商品的利润是 ;若每天可销出100件,则一天的总利润是 . 单件利润= - ;销售利润= × . ②某越剧团准备在市大剧院演出,该剧院能容纳600人.经调研,如果票价定为45元,那么门票可以全部售完,而门票价格每增加1元,售出的门票数就减少20张.当票价定为50元时,可以获得 元的门票收入. ③商场从厂家以每件21元的价格购进一批商品,若每件的售价为a元,则可卖出(350-10a)件,商场计划要赚450元,则每件商品的售价为多少元? 2如图,在△ABC中,∠C=90°,AB=10cm,AC=8cm,点P,Q同时由A,C两点出发,分别沿AC,CB方向移动,他们的速度都是2cm/s.
⑴设经过t秒后,那么在△PCQ中,此时线段,线段CQ长为 cm,PC长为 cm.
⑵经过几秒,P,Q相距2cm? 【新知探究】 例1.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查表明:这种台灯的售价每上涨1元,其销售量就将减少10个.为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个? 【变式】 1.某商店进了一批服装,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就将减少100件.如果商店销售这批服装要获利润12000元,那么这种服装售价应定为多少元?该商店应进这种服装多少件? 2.某种服装,平均每天可销售20件,每件盈利44元;若每件降价1元,则每天可多售5件.如果每天要盈利1600元,且尽快减少库存,每件应降价多少元? 例2.如图:在矩形ABCD中,AB=6cm,BC=12cm,点P从A点沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向C以2cm/s的速度移动,问:几秒后△PDQ的面积为28cm2吗? 【课内反馈】 1.某商店经销一种销售成本为每千克40元的水产品,椐市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克. 根据这种情况,请解答以下问题: ⑴当销售单价定为每千克55元时,求销售量和月销售利润; ⑵若在月销售成本不超过10 000元的情况下,要使月销售利润达到8000元,销售单价应定为多少? 2.新华商场销售甲冰箱,甲种冰箱每台进货价为2500元,市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,那么这种冰箱的定价应是多少 3. 如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积为20cm2? 【课时作业】 1.将进价为40元的商品按50元出售,每天能够卖出500个.经过市场调研,这种商品每涨价1元,就会少销售10个,为了赚取800元的利润,设销售价提高x元,那么这种商品的销售价为 元,销售量为 个,因此可列方程 . 2.如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿AC边向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动. ⑴若P,Q两点同时出发,几秒后可使△PQC的面积为8cm2? ⑵若P,Q两点同时出发,几秒后PQ的长度为3cm. 3.某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40~65元之间.市场调查发现:若每箱以50元销售,平均每天可销售90箱;价格每降低1元,平均每天多销售3箱;价格每升高1元,平均每天少销售3箱. ⑴写出平均每天销售y(箱)与每箱售价x(元)之间的关系式; ⑵求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的关系式; ⑶当每箱牛奶售价为多少时,平均每天的利润为900元? ⑷当每箱牛奶售价为多少时,平均每天的利润为1200元? 【课外延伸】 1.如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动. (1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2; (2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm. 2.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=4cm,AD=18cm,BC=21cm,点P从点A出发,沿边AD向点D以2cm/s的速度移动,点Q从点C出发沿边CB向点B以6cm/s的速度移动,P、Q同时出发,若有一点运动到端点时,另一点也随之停止.则①CD= cm; ②经过 秒后,PQ=CD. 3.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低元。 (1)填表(不需化简) 时间第一个月第二个月清仓时单价(元)8040销售量(件)200
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元? 4.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元. (1)若该公司当月售出3部汽车,则每部汽车的进价为 万元; (2)如果汽车的售价为28万元/部,该公司计划当月返利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
课 题 营销利润、动点问题
重点、难点 1、用方程解决实际问题的步骤,能处理营销利润问题. 2、寻找营销利润问题中的等量关系,列出方程. 3、以静代动;把动的点进行转换,变为线段的长度;
教学内容
Ⅰ.知识准备 1、①某商人将进价为每件8元的某种商品按每件10元出售,则一件商品的利润是 ;若每天可销出100件,则一天的总利润是 . 单件利润= - ;销售利润= × . ②某越剧团准备在市大剧院演出,该剧院能容纳600人.经调研,如果票价定为45元,那么门票可以全部售完,而门票价格每增加1元,售出的门票数就减少20张.当票价定为50元时,可以获得 元的门票收入. ③商场从厂家以每件21元的价格购进一批商品,若每件的售价为a元,则可卖出(350-10a)件,商场计划要赚450元,则每件商品的售价为多少元? 2如图,在△ABC中,∠C=90°,AB=10cm,AC=8cm,点P,Q同时由A,C两点出发,分别沿AC,CB方向移动,他们的速度都是2cm/s.
⑴设经过t秒后,那么在△PCQ中,此时线段,线段CQ长为 cm,PC长为 cm.
⑵经过几秒,P,Q相距2cm? 【新知探究】 例1.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查表明:这种台灯的售价每上涨1元,其销售量就将减少10个.为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个? 【变式】 1.某商店进了一批服装,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就将减少100件.如果商店销售这批服装要获利润12000元,那么这种服装售价应定为多少元?该商店应进这种服装多少件? 2.某种服装,平均每天可销售20件,每件盈利44元;若每件降价1元,则每天可多售5件.如果每天要盈利1600元,且尽快减少库存,每件应降价多少元? 例2.如图:在矩形ABCD中,AB=6cm,BC=12cm,点P从A点沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向C以2cm/s的速度移动,问:几秒后△PDQ的面积为28cm2吗? 【课内反馈】 1.某商店经销一种销售成本为每千克40元的水产品,椐市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克. 根据这种情况,请解答以下问题: ⑴当销售单价定为每千克55元时,求销售量和月销售利润; ⑵若在月销售成本不超过10 000元的情况下,要使月销售利润达到8000元,销售单价应定为多少? 2.新华商场销售甲冰箱,甲种冰箱每台进货价为2500元,市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,那么这种冰箱的定价应是多少 3. 如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积为20cm2? 【课时作业】 1.将进价为40元的商品按50元出售,每天能够卖出500个.经过市场调研,这种商品每涨价1元,就会少销售10个,为了赚取800元的利润,设销售价提高x元,那么这种商品的销售价为 元,销售量为 个,因此可列方程 . 2.如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿AC边向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动. ⑴若P,Q两点同时出发,几秒后可使△PQC的面积为8cm2? ⑵若P,Q两点同时出发,几秒后PQ的长度为3cm. 3.某商场销售某种品牌的纯牛奶,已知进价为每箱40元,生产厂家要求每箱售价在40~65元之间.市场调查发现:若每箱以50元销售,平均每天可销售90箱;价格每降低1元,平均每天多销售3箱;价格每升高1元,平均每天少销售3箱. ⑴写出平均每天销售y(箱)与每箱售价x(元)之间的关系式; ⑵求出商场平均每天销售这种牛奶的利润W(元)与每箱牛奶的售价x(元)之间的关系式; ⑶当每箱牛奶售价为多少时,平均每天的利润为900元? ⑷当每箱牛奶售价为多少时,平均每天的利润为1200元? 【课外延伸】 1.如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动. (1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2; (2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm. 2.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=4cm,AD=18cm,BC=21cm,点P从点A出发,沿边AD向点D以2cm/s的速度移动,点Q从点C出发沿边CB向点B以6cm/s的速度移动,P、Q同时出发,若有一点运动到端点时,另一点也随之停止.则①CD= cm; ②经过 秒后,PQ=CD. 3.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低元。 (1)填表(不需化简) 时间第一个月第二个月清仓时单价(元)8040销售量(件)200
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元? 4.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元. (1)若该公司当月售出3部汽车,则每部汽车的进价为 万元; (2)如果汽车的售价为28万元/部,该公司计划当月返利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
同课章节目录
