四川省泸州市泸县2022-2023学年高二下学期开学考试数学(理)试题(含答案)
文档属性
| 名称 | 四川省泸州市泸县2022-2023学年高二下学期开学考试数学(理)试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 513.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-03 20:19:35 | ||
图片预览


文档简介
泸县2022-2023学年高二下学期开学考试
理科数学
本试卷共4页,22小题,满分150分。考试用时120分钟。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为
A.11 B.12 C.13 D.14
2.抛物线 的焦点坐标是
A. B. C. D.
3.已知两直线与,则与间的距离为
A. B. C. D.
4.执行如图所示的程序框图,如果输入的值为,则输出
A.2 B. C.3 D.
5.用这3个数组成没有重复数字的三位数,则事件“这个三位数是偶数”与事件“这个三位数大于342”
A.是互斥但不对立事件 B.不是互斥事件
C.是对立事件 D.是不可能事件
6.“”是“方程是圆的方程”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.命题若,且,则,命题在中,若,则.下列命题中为真命题的是
A. B. C. D.
8.在矩形中,,,平面,,则与平面所成角是.
A. B. C. D.
9.已知直线:与曲线有两个公共点,则实数的取值范围是
A. B. C. D.
10.已知三棱锥的各顶点都在同一球面上,且平面,,,,若该棱锥的体积为,则此球的表面积为
A. B. C. D.
11.设,点为双曲线的左顶点,线段交双曲线一条渐近线于点,且满足,则该双曲线的离心率为
A. B. C. D.
12.如图,在单位正方体中,点P在线段上运动,给出以下四个命题:
异面直线与间的距离为定值;
三棱锥的体积为定值;
异面直线与直线所成的角为定值;
二面角的大小为定值.
其中真命题有
A.1个 B.2个 C.3个 D.4个
二、填空题:本题共4小题,每小题5分,共20分
13.已知圆:,圆:,则圆与圆的位置关系是______.
14.某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
15.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.
16.过抛物线的焦点F作斜率大于0的直线l交抛物线于A,B两点(A在B的上方),且l与准线交于点C,若,则_________.
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知:,:,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
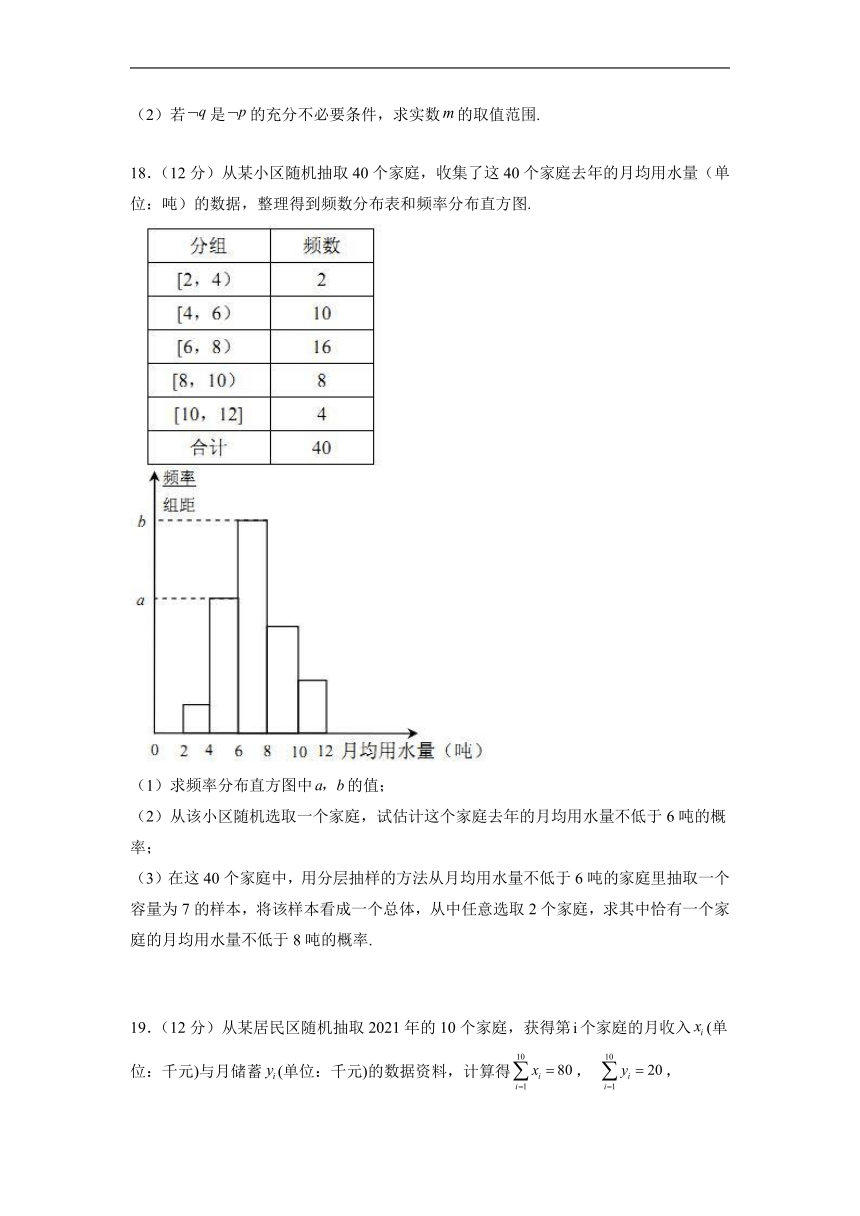
18.(12分)从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
(1)求频率分布直方图中的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
19.(12分)从某居民区随机抽取2021年的10个家庭,获得第个家庭的月收入(单位:千元)与月储蓄(单位:千元)的数据资料,计算得, , , .
(1)求家庭的月储蓄对月收入的线性回归方程;
(2)判断变量与之间是正相关还是负相关;
(3)利用(1)中的回归方程,分析2021年该地区居民月收入与月储蓄之间的变化情况,并预测当该居民区某家庭月收入为7千元,该家庭的月储蓄额.附:线性回归方程系数公式.
中,,, 其中,为样本平均值.
20.(12分)已知抛物线y2=2px(p>0)的焦点为F,过F且与x轴垂直的直线交该抛物线于A,B两
点,|AB|=4.
(1)求抛物线的方程;
(2)过点F的直线l交抛物线于P,Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).
21.(12分)如图所示,⊥平面,四边形为矩形,,.
(1)求证:∥平面;
(2)求平面与平面所成锐二面角的余弦值.
22.(12分)已知椭圆的离心率为,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为.
(1)求椭圆的方程;
(2)设直线与椭圆交于、两点,若以为直径的圆经过椭圆的右顶点,求的值.
泸县2022-2023学年高二下学期开学考试
理科数学参考答案:
1.B 2.D 3.B 4.B 5.B 6.A 7.A 8.A 9.B 10.B 11.D 12.D
13.相交 14. 15.[-1,+∞) 16.2
17.解:由,解得,所以:,
又,且,解得,所以:.
(1)当时,:,
因为为真,所以都为真,所以.
(2)因为是的充分不必要条件,所以是的充分不必要条件,
因为:,:,所以,解得.
18.解:(1)因为样本中家庭月均用水量在上的频率为,
在上的频率为,所以,
(2)根据频数分布表,40个家庭中月均用水量不低于6吨的家庭共有16+8+4=28个,
所以样本中家庭月均用水量不低于6吨的概率是.
利用样本估计总体,从该小区随机选取一个家庭,可估计这个家庭去年的月均用水量不低于6吨的概率约为0.7
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,
则在上应抽取人,记为,
在上应抽取人,记为,
在上应抽取人,记为
设“从中任意选取2个家庭,求其中恰有1个家庭的月均用水量不低于8吨”为事件,
则所有基本事件有:
,共21种.
事件包含的基本事件有:,
共12种.
所以其中恰有一个家庭的月均用水量不低于8吨的概率为
19.(1)由题意知n=10,,
则,所以所求回归方程为=0.3x-0.4.
(2)因为,所以变量y的值随x的值增加而增加,故x与y之间是正相关.
(3)将x=7代入回归方程可以预测该家庭的月储蓄为=0.3×7-0.4=1.7(千元).
20.解:(1)由抛物线的定义得到准线的距离都是p ,
所以|AB|=2p=4,所以抛物线的方程为y2=4x.
(2)设直线l的方程为y=k(x-1),P(x1,y1),Q(x2,y2).
因为直线l与抛物线有两个交点,
所以k≠0,得,代入y2=4x,得,且恒成立,
则,y1y2=-4,所以.
又点O到直线l的距离,
所以,解得,即.
21解:(1)证明:四边形为矩形,∴,又,平面,平面ADE,故平面ADE,平面ADE,
又平面BFC,∴平面BFC平面ADE,
∵平面BFC,∴∥平面;
(2)建立空间直角坐标系如图,则,
设平面CDF的法向量为,则,
取得,
平面的法向量为,设平面与平面所成锐二面角为,
则,故平面与平面所成锐二面角的余弦值为
22.解:(1)因为椭圆上一点和它的两个焦点构成的三角形周长为,
所以,
又椭圆的离心率为,即,
所以,可得,,所以,椭圆的方程为;
(2)由,消去得,
设、,则有,,①.
因为以为直径的圆过点,所以.
由,,得.
将,代入上式,
得.
将①代入上式,可得,
整理可得,解得或.
理科数学
本试卷共4页,22小题,满分150分。考试用时120分钟。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为
A.11 B.12 C.13 D.14
2.抛物线 的焦点坐标是
A. B. C. D.
3.已知两直线与,则与间的距离为
A. B. C. D.
4.执行如图所示的程序框图,如果输入的值为,则输出
A.2 B. C.3 D.
5.用这3个数组成没有重复数字的三位数,则事件“这个三位数是偶数”与事件“这个三位数大于342”
A.是互斥但不对立事件 B.不是互斥事件
C.是对立事件 D.是不可能事件
6.“”是“方程是圆的方程”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.命题若,且,则,命题在中,若,则.下列命题中为真命题的是
A. B. C. D.
8.在矩形中,,,平面,,则与平面所成角是.
A. B. C. D.
9.已知直线:与曲线有两个公共点,则实数的取值范围是
A. B. C. D.
10.已知三棱锥的各顶点都在同一球面上,且平面,,,,若该棱锥的体积为,则此球的表面积为
A. B. C. D.
11.设,点为双曲线的左顶点,线段交双曲线一条渐近线于点,且满足,则该双曲线的离心率为
A. B. C. D.
12.如图,在单位正方体中,点P在线段上运动,给出以下四个命题:
异面直线与间的距离为定值;
三棱锥的体积为定值;
异面直线与直线所成的角为定值;
二面角的大小为定值.
其中真命题有
A.1个 B.2个 C.3个 D.4个
二、填空题:本题共4小题,每小题5分,共20分
13.已知圆:,圆:,则圆与圆的位置关系是______.
14.某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
15.设函数f(x)=|x+a|,g(x)=x-1,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.
16.过抛物线的焦点F作斜率大于0的直线l交抛物线于A,B两点(A在B的上方),且l与准线交于点C,若,则_________.
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知:,:,其中.
(1)若且为真,求的取值范围;
(2)若是的充分不必要条件,求实数的取值范围.
18.(12分)从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
(1)求频率分布直方图中的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
19.(12分)从某居民区随机抽取2021年的10个家庭,获得第个家庭的月收入(单位:千元)与月储蓄(单位:千元)的数据资料,计算得, , , .
(1)求家庭的月储蓄对月收入的线性回归方程;
(2)判断变量与之间是正相关还是负相关;
(3)利用(1)中的回归方程,分析2021年该地区居民月收入与月储蓄之间的变化情况,并预测当该居民区某家庭月收入为7千元,该家庭的月储蓄额.附:线性回归方程系数公式.
中,,, 其中,为样本平均值.
20.(12分)已知抛物线y2=2px(p>0)的焦点为F,过F且与x轴垂直的直线交该抛物线于A,B两
点,|AB|=4.
(1)求抛物线的方程;
(2)过点F的直线l交抛物线于P,Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).
21.(12分)如图所示,⊥平面,四边形为矩形,,.
(1)求证:∥平面;
(2)求平面与平面所成锐二面角的余弦值.
22.(12分)已知椭圆的离心率为,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为.
(1)求椭圆的方程;
(2)设直线与椭圆交于、两点,若以为直径的圆经过椭圆的右顶点,求的值.
泸县2022-2023学年高二下学期开学考试
理科数学参考答案:
1.B 2.D 3.B 4.B 5.B 6.A 7.A 8.A 9.B 10.B 11.D 12.D
13.相交 14. 15.[-1,+∞) 16.2
17.解:由,解得,所以:,
又,且,解得,所以:.
(1)当时,:,
因为为真,所以都为真,所以.
(2)因为是的充分不必要条件,所以是的充分不必要条件,
因为:,:,所以,解得.
18.解:(1)因为样本中家庭月均用水量在上的频率为,
在上的频率为,所以,
(2)根据频数分布表,40个家庭中月均用水量不低于6吨的家庭共有16+8+4=28个,
所以样本中家庭月均用水量不低于6吨的概率是.
利用样本估计总体,从该小区随机选取一个家庭,可估计这个家庭去年的月均用水量不低于6吨的概率约为0.7
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,
则在上应抽取人,记为,
在上应抽取人,记为,
在上应抽取人,记为
设“从中任意选取2个家庭,求其中恰有1个家庭的月均用水量不低于8吨”为事件,
则所有基本事件有:
,共21种.
事件包含的基本事件有:,
共12种.
所以其中恰有一个家庭的月均用水量不低于8吨的概率为
19.(1)由题意知n=10,,
则,所以所求回归方程为=0.3x-0.4.
(2)因为,所以变量y的值随x的值增加而增加,故x与y之间是正相关.
(3)将x=7代入回归方程可以预测该家庭的月储蓄为=0.3×7-0.4=1.7(千元).
20.解:(1)由抛物线的定义得到准线的距离都是p ,
所以|AB|=2p=4,所以抛物线的方程为y2=4x.
(2)设直线l的方程为y=k(x-1),P(x1,y1),Q(x2,y2).
因为直线l与抛物线有两个交点,
所以k≠0,得,代入y2=4x,得,且恒成立,
则,y1y2=-4,所以.
又点O到直线l的距离,
所以,解得,即.
21解:(1)证明:四边形为矩形,∴,又,平面,平面ADE,故平面ADE,平面ADE,
又平面BFC,∴平面BFC平面ADE,
∵平面BFC,∴∥平面;
(2)建立空间直角坐标系如图,则,
设平面CDF的法向量为,则,
取得,
平面的法向量为,设平面与平面所成锐二面角为,
则,故平面与平面所成锐二面角的余弦值为
22.解:(1)因为椭圆上一点和它的两个焦点构成的三角形周长为,
所以,
又椭圆的离心率为,即,
所以,可得,,所以,椭圆的方程为;
(2)由,消去得,
设、,则有,,①.
因为以为直径的圆过点,所以.
由,,得.
将,代入上式,
得.
将①代入上式,可得,
整理可得,解得或.
同课章节目录
