物理人教版(2019)选择性必修第一册2.1简谐运动(共14张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.1简谐运动(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-03 20:59:20 | ||
图片预览






文档简介
(共14张PPT)
简谐运动
选择性必修一
CONTENTS
目录
1
机械振动
2
弹簧振子
3
简谐运动
4
函数表达式
01
机械振动
机械振动
物体或物体的一部分在一个位置附近的往复运动称为机械振动,简称振动
判断以下哪种运动是简谐振动?
x
x
x
x
t
t
t
t
02
弹簧振子
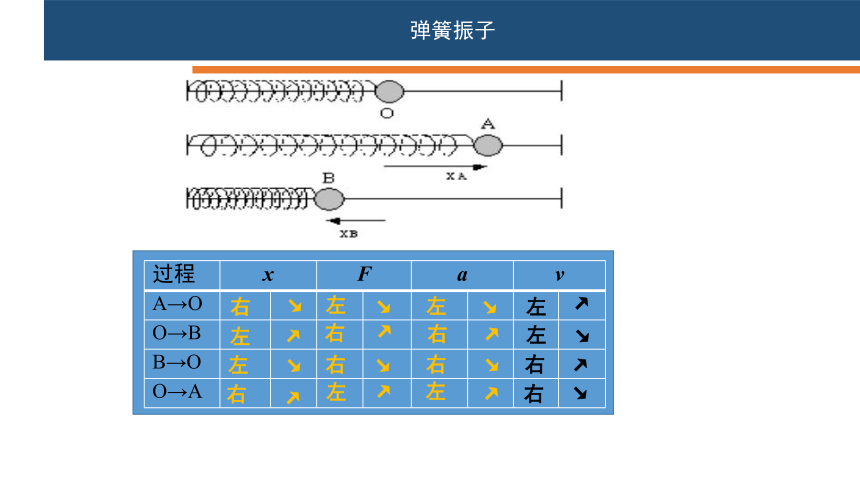
弹簧振子
弹簧振子需满足以下条件
①在弹性限度内
②小球看成质点
③忽略弹簧质量
④忽略摩擦力
理想化模型
平衡位置:物体运动方向上合力为0/振动停止时所在的位置
位移:由平衡位置指向振子所在位置的有向线段
过程 x F a v A→O
O→B
B→O
O→A
右
↘
↗
左
右
右
右
右
右
右
右
左
左
左
左
左
左
左
↘
↘
↘
↘
↘
↗
↗
↗
↗
↗
↗
↗
↘
↘
弹簧振子
03
简谐运动
力学定义
如果物体在运动方向上所受的力与偏离平衡位置位移的大小成正比,并且总指向平衡位置,质点的运动就是简谐振动。
运动定义
如果物体位移与时间的关系遵从正弦函数规律,即它的振动图像是一条正弦曲线,这样的振动是一种简谐振动。
简谐运动的位移随时间按正弦规律变化,所以它不是匀变速运动,是变力作用下的变加速运动。
回复力:物体在运动方向上的所受的力,使物体在平衡位置附近往复运动。
简谐运动
简谐运动
试证明下面两种运动是简谐运动。
在简谐运动中,系统的动能和势能之和都是一定的,遵守机械能守恒定律。
04
函数表达式
函数表达式
做简谐运动的物体的位移x与运动时间t之间满足正弦函数关系,因此,位移x的一般函数
表达式可写为:
A:振幅,偏离平衡位置的最大距离,反映了振动系统的总机械能
ω:圆频率
φ:初相
ωt+φ:相位
T :周期 一次全振动所需时间 f:单位时间内完成全振动的次数
函数表达式
振动周期与振幅无关。
感谢聆听
主讲人 2023
简谐运动
选择性必修一
CONTENTS
目录
1
机械振动
2
弹簧振子
3
简谐运动
4
函数表达式
01
机械振动
机械振动
物体或物体的一部分在一个位置附近的往复运动称为机械振动,简称振动
判断以下哪种运动是简谐振动?
x
x
x
x
t
t
t
t
02
弹簧振子
弹簧振子
弹簧振子需满足以下条件
①在弹性限度内
②小球看成质点
③忽略弹簧质量
④忽略摩擦力
理想化模型
平衡位置:物体运动方向上合力为0/振动停止时所在的位置
位移:由平衡位置指向振子所在位置的有向线段
过程 x F a v A→O
O→B
B→O
O→A
右
↘
↗
左
右
右
右
右
右
右
右
左
左
左
左
左
左
左
↘
↘
↘
↘
↘
↗
↗
↗
↗
↗
↗
↗
↘
↘
弹簧振子
03
简谐运动
力学定义
如果物体在运动方向上所受的力与偏离平衡位置位移的大小成正比,并且总指向平衡位置,质点的运动就是简谐振动。
运动定义
如果物体位移与时间的关系遵从正弦函数规律,即它的振动图像是一条正弦曲线,这样的振动是一种简谐振动。
简谐运动的位移随时间按正弦规律变化,所以它不是匀变速运动,是变力作用下的变加速运动。
回复力:物体在运动方向上的所受的力,使物体在平衡位置附近往复运动。
简谐运动
简谐运动
试证明下面两种运动是简谐运动。
在简谐运动中,系统的动能和势能之和都是一定的,遵守机械能守恒定律。
04
函数表达式
函数表达式
做简谐运动的物体的位移x与运动时间t之间满足正弦函数关系,因此,位移x的一般函数
表达式可写为:
A:振幅,偏离平衡位置的最大距离,反映了振动系统的总机械能
ω:圆频率
φ:初相
ωt+φ:相位
T :周期 一次全振动所需时间 f:单位时间内完成全振动的次数
函数表达式
振动周期与振幅无关。
感谢聆听
主讲人 2023
