16.1.1 分式 学案
图片预览


文档简介
中小学教育资源及组卷应用平台
16.1.1 分式 导学案
课题 16.1.1 分式 单元 第16单元 学科 数学 年级 八年级(下)
教材分析 了解分式和整式的概念,掌握它们的区别 ( 21cnjy )。能正确判断一个代数式是否为分式,分清分式和整式的区别,了解有理式的概念.理解并掌握判断一个分式有意义、无意义及值为零的方法.1世
核心素养分析 初步掌握整式和分式的思想方法,培养学生分析、归纳、概括的能力.在数学学习活动中获得成功的体验,体会数学在现实生活中的应用.通过对比分数和分式基本性质的异同点,渗透类比的思想方法,学会用运动、变化的观点分析问题.
学习目标 1.使学生了解分式的概念,有理式的概念.2.理解分式有意义的条件,分式的值为零的条件;能熟练地求出分式有意义的条件,分式的值为零的条件.
重点 准确理解分式的意义,能熟练地求出分式有意义的条件,分式的值为零的条件.
难点 归纳分式的概念及探索分式有意义的条件.
教学过程
课前预学 引入思考回顾:(1)分数的概念: 。(2)分数有意义的条件: 。请你来填一填:(1)面积为2平方米的长方形的长为3米,则它的宽为_______米;(2)面积为S平方米的长方形的长为a米,则它的宽为_______米;(3)已知正方形的周长是a cm,则一边的长是____cm,面积是_______cm2;(4)一箱苹果售价P元,总重m千克,箱重n千克,则每千克苹果的售价是______元.在上面所列出的代数式 中,哪些是整式?哪些不是?它们之间有什么区别?请同学们交流你们发现的结论.归纳分式的概念: 。注意分式的特点:① ; ② 。思考:什么叫做有理式?有理式如何分类?
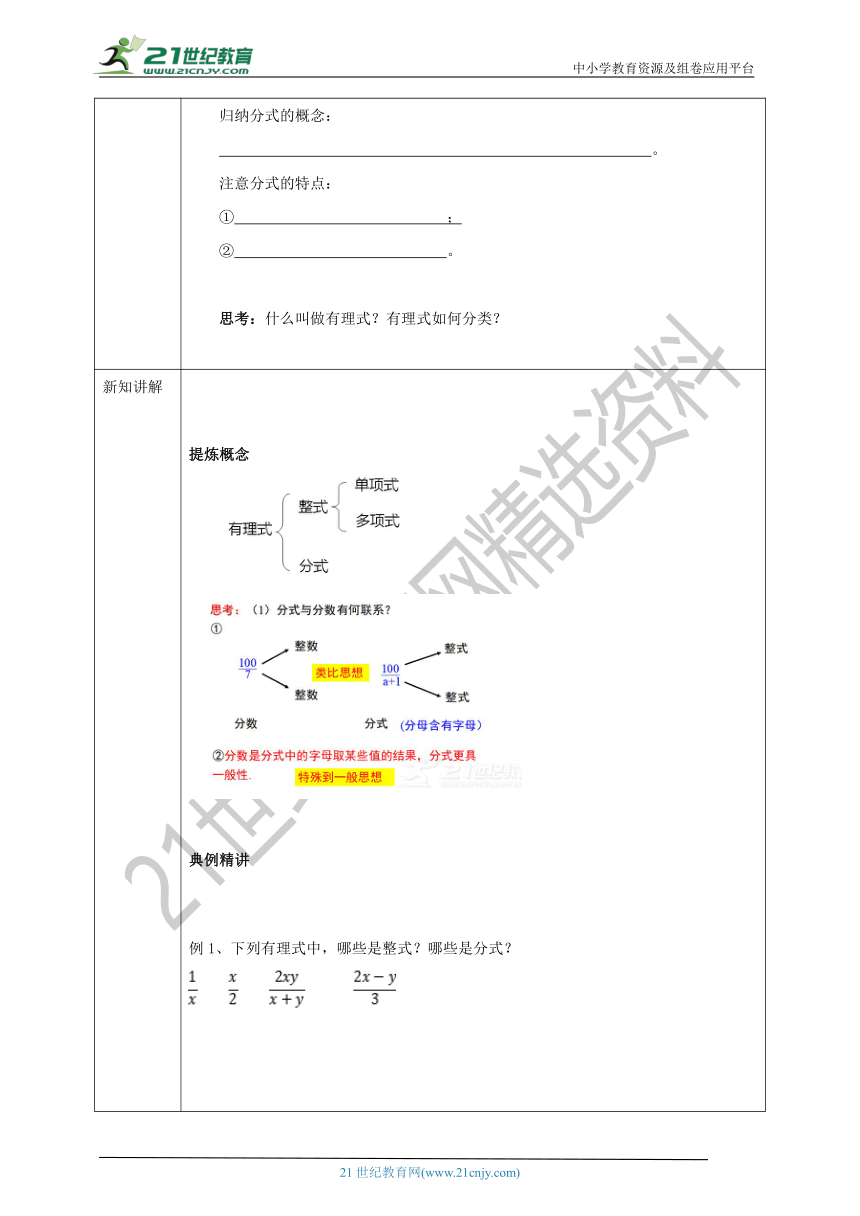
新知讲解 提炼概念典例精讲 例1、下列有理式中,哪些是整式?哪些是分式? 例2 (1)当x为何值时,分式 有意义 (2)当x为何值时,分式有意义 归纳:分式有意义: 分式无意义: 分式的值为0: 例3 当x是什么数时,分式的值等于零?
课堂练习 巩固训练 1.下列代数式中,属于分式的有( ) 2.当a=-1时,分式 的值( ) A.没有意义 B.等于零 C.等于1 D.等于-13. 已知分式 有意义,则x应满足的条件是 ( )A.x≠1 B.x≠2 C.x≠1且x≠2 D.以上结果都不对4.(1)当x______时,分式 有意义.(2)当x ______时,分式 的值为零.5.在分式 中,当x为何值时,分式有意义?分式的值为零? 分式 的值能等于0吗?说明理由.
7.已知分式 ,当x=2时,分式的值为零;当x=-2时,分式没有意义,求a+b的值.答案引入思考 请你来填一填:整式有:①③④ ,整式的特点是分母不含字母;不是整式的有:②⑤,形如 (A,B是整式,且B中含有字母,B≠0 ) 的式子, 叫做分式.其中A叫做分式的分子,B叫做分式的分母.有理式的分类:提炼概念典例精讲 例1 解:和是整式,和是分式.例2 解:(1)分母x-1≠0,即x≠1,所以,当x≠1时,分式有意义.例2 解:(1)分母x-1≠0,即x≠1,所以,当x≠1时,分式有意义.(2)分母2x+3≠0,即x≠,所以,当 x≠时,分式有意义.例 3解:分式的值等于零的条件是: 由①得x≠ .由②得.所以,当时,分式的值等于零.巩固训练1. C2.A3. C4. (1)≠1/2 (2)=25. 答:当x ≠ 3时,该分式有意义;当x=-3时,该分式的值为零.6.答:不能.因为 必须x=-3,而x=-3时,分母x2-x-12=0,分式无意义.7.解:∵x=2时,分式的值为零,∴2-b=0,解得,b=2.∵x=-2时,分式没有意义,∴2×(-2)+a=0,解得,a=4.∴a+b=6.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
16.1.1 分式 导学案
课题 16.1.1 分式 单元 第16单元 学科 数学 年级 八年级(下)
教材分析 了解分式和整式的概念,掌握它们的区别 ( 21cnjy )。能正确判断一个代数式是否为分式,分清分式和整式的区别,了解有理式的概念.理解并掌握判断一个分式有意义、无意义及值为零的方法.1世
核心素养分析 初步掌握整式和分式的思想方法,培养学生分析、归纳、概括的能力.在数学学习活动中获得成功的体验,体会数学在现实生活中的应用.通过对比分数和分式基本性质的异同点,渗透类比的思想方法,学会用运动、变化的观点分析问题.
学习目标 1.使学生了解分式的概念,有理式的概念.2.理解分式有意义的条件,分式的值为零的条件;能熟练地求出分式有意义的条件,分式的值为零的条件.
重点 准确理解分式的意义,能熟练地求出分式有意义的条件,分式的值为零的条件.
难点 归纳分式的概念及探索分式有意义的条件.
教学过程
课前预学 引入思考回顾:(1)分数的概念: 。(2)分数有意义的条件: 。请你来填一填:(1)面积为2平方米的长方形的长为3米,则它的宽为_______米;(2)面积为S平方米的长方形的长为a米,则它的宽为_______米;(3)已知正方形的周长是a cm,则一边的长是____cm,面积是_______cm2;(4)一箱苹果售价P元,总重m千克,箱重n千克,则每千克苹果的售价是______元.在上面所列出的代数式 中,哪些是整式?哪些不是?它们之间有什么区别?请同学们交流你们发现的结论.归纳分式的概念: 。注意分式的特点:① ; ② 。思考:什么叫做有理式?有理式如何分类?
新知讲解 提炼概念典例精讲 例1、下列有理式中,哪些是整式?哪些是分式? 例2 (1)当x为何值时,分式 有意义 (2)当x为何值时,分式有意义 归纳:分式有意义: 分式无意义: 分式的值为0: 例3 当x是什么数时,分式的值等于零?
课堂练习 巩固训练 1.下列代数式中,属于分式的有( ) 2.当a=-1时,分式 的值( ) A.没有意义 B.等于零 C.等于1 D.等于-13. 已知分式 有意义,则x应满足的条件是 ( )A.x≠1 B.x≠2 C.x≠1且x≠2 D.以上结果都不对4.(1)当x______时,分式 有意义.(2)当x ______时,分式 的值为零.5.在分式 中,当x为何值时,分式有意义?分式的值为零? 分式 的值能等于0吗?说明理由.
7.已知分式 ,当x=2时,分式的值为零;当x=-2时,分式没有意义,求a+b的值.答案引入思考 请你来填一填:整式有:①③④ ,整式的特点是分母不含字母;不是整式的有:②⑤,形如 (A,B是整式,且B中含有字母,B≠0 ) 的式子, 叫做分式.其中A叫做分式的分子,B叫做分式的分母.有理式的分类:提炼概念典例精讲 例1 解:和是整式,和是分式.例2 解:(1)分母x-1≠0,即x≠1,所以,当x≠1时,分式有意义.例2 解:(1)分母x-1≠0,即x≠1,所以,当x≠1时,分式有意义.(2)分母2x+3≠0,即x≠,所以,当 x≠时,分式有意义.例 3解:分式的值等于零的条件是: 由①得x≠ .由②得.所以,当时,分式的值等于零.巩固训练1. C2.A3. C4. (1)≠1/2 (2)=25. 答:当x ≠ 3时,该分式有意义;当x=-3时,该分式的值为零.6.答:不能.因为 必须x=-3,而x=-3时,分母x2-x-12=0,分式无意义.7.解:∵x=2时,分式的值为零,∴2-b=0,解得,b=2.∵x=-2时,分式没有意义,∴2×(-2)+a=0,解得,a=4.∴a+b=6.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
