简易方程(二)行程问题(课件)沪教版五年级下册数学(共17张PPT)
文档属性
| 名称 | 简易方程(二)行程问题(课件)沪教版五年级下册数学(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-04 06:37:53 | ||
图片预览


文档简介
(共17张PPT)
第三章:简易方程(二)
行程问题
五年级下册
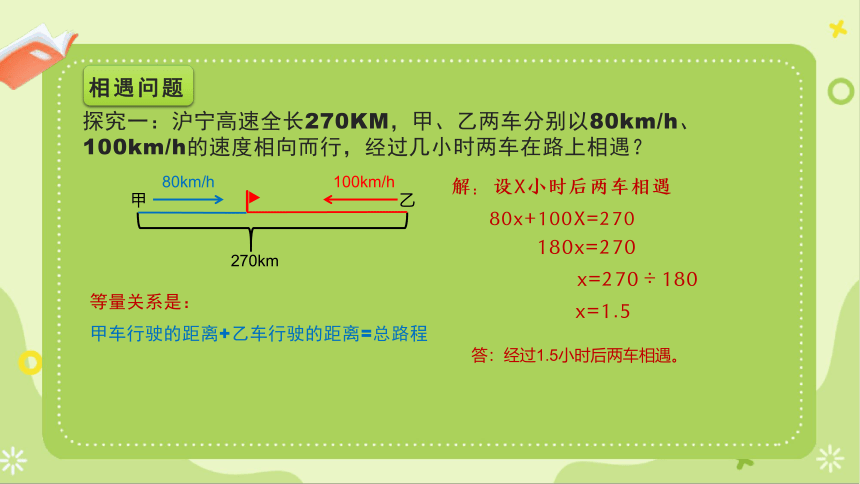
探究一:沪宁高速全长270KM,甲、乙两车分别以80km/h、100km/h的速度相向而行,经过几小时两车在路上相遇?
解:设X小时后两车相遇
等量关系是:
甲车行驶的距离+乙车行驶的距离=总路程
80x+100X=270
180x=270
x=270÷180
x=1.5
相遇问题
甲
乙
80km/h
100km/h
270km
答:经过1.5小时后两车相遇。
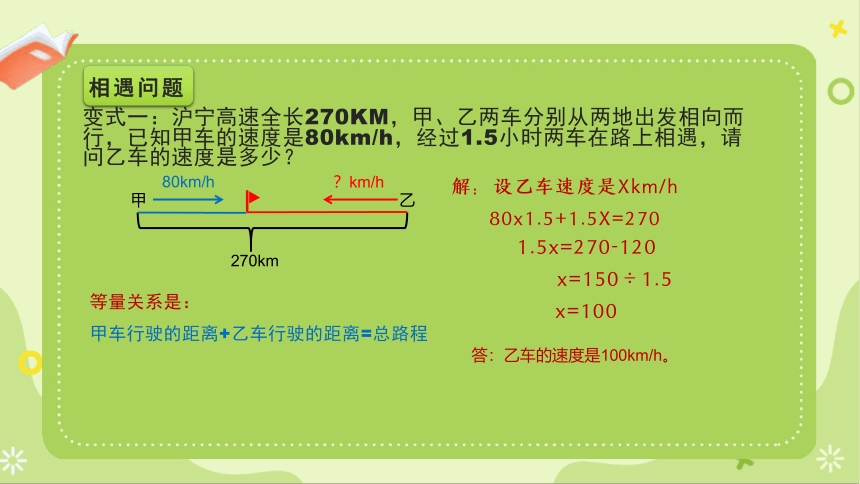
变式一:沪宁高速全长270KM,甲、乙两车分别从两地出发相向而行,已知甲车的速度是80km/h,经过1.5小时两车在路上相遇,请问乙车的速度是多少?
解:设乙车速度是Xkm/h
等量关系是:
甲车行驶的距离+乙车行驶的距离=总路程
80x1.5+1.5X=270
1.5x=270-120
x=150÷1.5
x=100
相遇问题
甲
乙
80km/h
?km/h
270km
答:乙车的速度是100km/h。
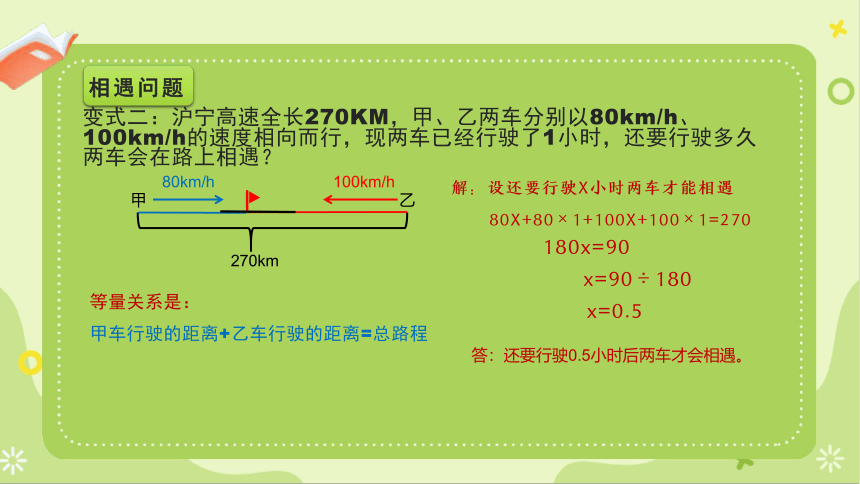
变式二:沪宁高速全长270KM,甲、乙两车分别以80km/h、100km/h的速度相向而行,现两车已经行驶了1小时,还要行驶多久两车会在路上相遇?
解:设还要行驶X小时两车才能相遇
等量关系是:
甲车行驶的距离+乙车行驶的距离=总路程
80X+80×1+100X+100×1=270
180x=90
x=90÷180
x=0.5
相遇问题
甲
乙
80km/h
100km/h
270km
答:还要行驶0.5小时后两车才会相遇。
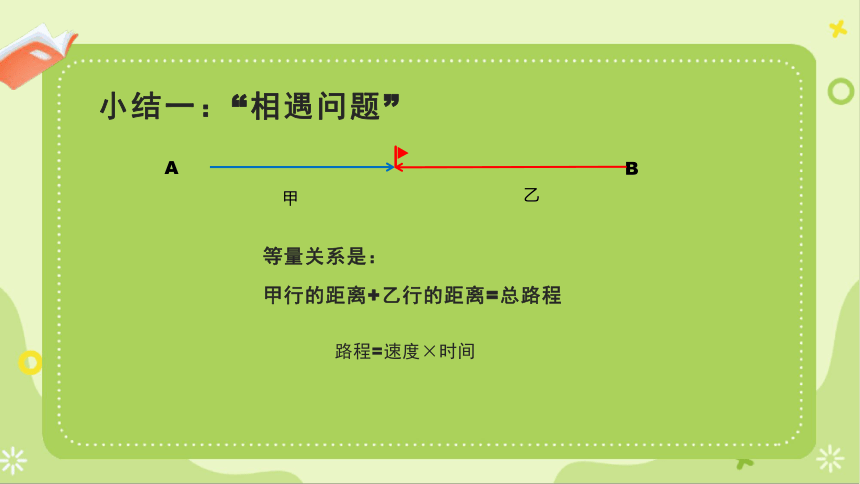
小结一:“相遇问题”
等量关系是:
甲行的距离+乙行的距离=总路程
路程=速度×时间
A
B
甲
乙
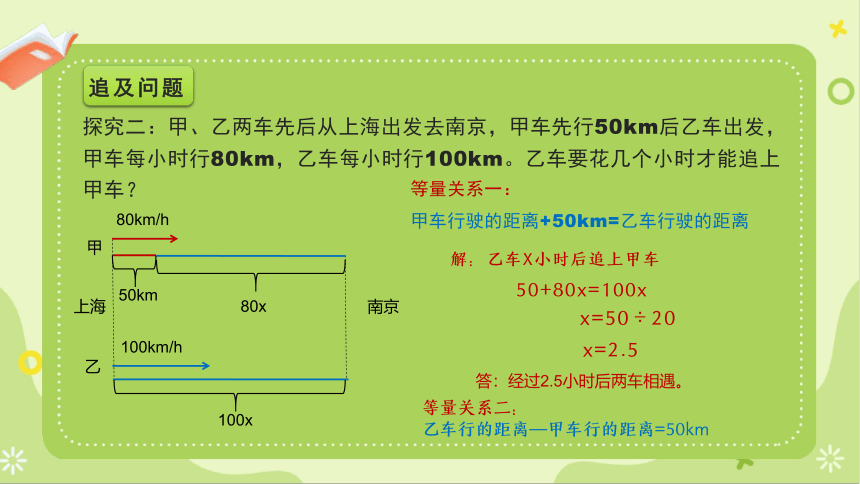
探究二:甲、乙两车先后从上海出发去南京,甲车先行50km后乙车出发,甲车每小时行80km,乙车每小时行100km。乙车要花几个小时才能追上甲车?
解:乙车X小时后追上甲车
等量关系一:
甲车行驶的距离+50km=乙车行驶的距离
50+80x=100x
x=50÷20
x=2.5
追及问题
答:经过2.5小时后两车相遇。
上海
南京
乙
甲
80km/h
100km/h
50km
100x
80x
等量关系二:
乙车行的距离—甲车行的距离=50km
探究二:甲、乙两车先后从上海出发去南京,甲车先行50km后乙车出发,甲车每小时行80km,乙车每小时行100km。乙车要花几个小时才能追上甲车?
等量关系二:
乙车行的距离—甲车行的距离=50km
解:乙车X小时后追上甲车
100x—80x=50
x=50÷20
x=2.5
答:经过2.5小时后两车相遇。
变式三:甲、乙两车同时从上海出发去南京,甲车在距离乙车前面50km的地方出发,甲车每小时行80km,乙车每小时行100km。乙车要花几个小时才能追上甲车?
解:乙车X小时后追上甲车
等量关系一:
甲车行驶的距离=乙车行驶的距离+50km
50+80x=100x
x=50÷20
x=2.5
追及问题
答:经过2.5小时后两车相遇。
上海
南京
乙
甲
80km/h
100km/h
50km
100x
80x
等量关系二:
乙车行的距离—甲车行的距离=50km
小结二:“追及问题”
路程=速度×时间
乙
甲
a
等量关系一:
甲车行驶的距离+a=乙车行驶的距离
等量关系二:
乙车行的距离—甲车行的距离=a
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设宿舍有X间,则学生有4X人
等量关系是:
每间住4人的总人数=每间住6人的总人数
6X-30=4X
2X=30
X=15
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设宿舍有X间,则住宿的学生可以用4X表示或者6X-30表示
分配过程中的总数不变
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设宿舍有X间,则学生有4X人
等量关系是:
每间住6人的总人数-每间住4人的总人数=多出来的5间房×每个房间住6个人
6X-4X=5×6
2X=30
X=15
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设宿舍有X间,则住宿的学生可以用4X表示或者6X-30表示
分配过程中的总数不变
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设宿舍有X间,则学生有4X人
等量关系是:
每间住6人的总人数-每间住4人的总人数=多出来的5间房×每个房间住6个人
6X-4X=5×6
2X=30
X=15
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设宿舍有X间,则住宿的学生可以用4X表示或者6X-30表示
分配过程中的总数不变
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设学生有X人,
则宿舍有X÷4或者(X÷6+5)间
等量关系是:
每间房间住4人的房间数=每间房间住6人的总房间数+多出来的5间房
X÷4=X÷6+5
6X=4X+5×24
X=60
宿舍:60÷4=15(间)
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设学生共有X人
分配过程中的总数不变
宿舍房间数可以用X÷4或者(X÷6+5)
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
盈亏问题
分析
每个房间住6个人比每个房间住4个人少住了5个房间,但每次多住2个人
所以住6个人的房间数是4×5÷2=10(间)
总的房间数是10+5=15(间)
分配过程中的总数不变
新生人数是15×4=60(人)
或者(15-5)×6=60(人)
答:一共有15间宿舍,60个学生。
探究四:一盒糖平均分给几个小朋友,如果每人分6颗还剩下14颗,如果每人分8颗,那么正好分完,一共有几个小朋友?这盒糖有多少颗?
解:设一共有X个小朋友,则一共有8X颗糖
等量关系是:
分6颗糖的总人数=分8颗糖的总人数
8X=6X+14
2X=14
X=7
盈亏问题
答:一共有7个小朋友,这盒糖有56颗。
总糖数不变
假设一共有X个小朋友
分配过程中的总数不变
如果每个人分6颗,那么一共有(6X+14)颗糖
如果每个人分8颗,那么一共有8X颗糖
糖果总数:8×7=56(颗)
探究四:一盒糖平均分给几个小朋友,如果每人分6颗还剩下14颗,如果每人分8颗,那么正好分完,一共有几个小朋友?这盒糖有多少颗?
盈亏问题
分析
每次6颗糖比每次分8颗糖,最终多于下14颗,然而每次却少分了两颗
所以分糖的次数是14÷(8-6)=7(次)
分配过程中的总数不变
共有糖: 6×7+14=56(颗)
或者8×7=56(颗)
答:一共有7个小朋友,共有56颗糖
小结:
列方程解决问题的关键是什么?
找出未知量和已知量的等量关系
列方程解决问题的一般步骤是什么?
1、设未知数,用字母表示未知数,用未知数表示相关量
2、找出未知量与已知量的等量关系,列方程
3、解方程
4、验算并写出答
第三章:简易方程(二)
行程问题
五年级下册
探究一:沪宁高速全长270KM,甲、乙两车分别以80km/h、100km/h的速度相向而行,经过几小时两车在路上相遇?
解:设X小时后两车相遇
等量关系是:
甲车行驶的距离+乙车行驶的距离=总路程
80x+100X=270
180x=270
x=270÷180
x=1.5
相遇问题
甲
乙
80km/h
100km/h
270km
答:经过1.5小时后两车相遇。
变式一:沪宁高速全长270KM,甲、乙两车分别从两地出发相向而行,已知甲车的速度是80km/h,经过1.5小时两车在路上相遇,请问乙车的速度是多少?
解:设乙车速度是Xkm/h
等量关系是:
甲车行驶的距离+乙车行驶的距离=总路程
80x1.5+1.5X=270
1.5x=270-120
x=150÷1.5
x=100
相遇问题
甲
乙
80km/h
?km/h
270km
答:乙车的速度是100km/h。
变式二:沪宁高速全长270KM,甲、乙两车分别以80km/h、100km/h的速度相向而行,现两车已经行驶了1小时,还要行驶多久两车会在路上相遇?
解:设还要行驶X小时两车才能相遇
等量关系是:
甲车行驶的距离+乙车行驶的距离=总路程
80X+80×1+100X+100×1=270
180x=90
x=90÷180
x=0.5
相遇问题
甲
乙
80km/h
100km/h
270km
答:还要行驶0.5小时后两车才会相遇。
小结一:“相遇问题”
等量关系是:
甲行的距离+乙行的距离=总路程
路程=速度×时间
A
B
甲
乙
探究二:甲、乙两车先后从上海出发去南京,甲车先行50km后乙车出发,甲车每小时行80km,乙车每小时行100km。乙车要花几个小时才能追上甲车?
解:乙车X小时后追上甲车
等量关系一:
甲车行驶的距离+50km=乙车行驶的距离
50+80x=100x
x=50÷20
x=2.5
追及问题
答:经过2.5小时后两车相遇。
上海
南京
乙
甲
80km/h
100km/h
50km
100x
80x
等量关系二:
乙车行的距离—甲车行的距离=50km
探究二:甲、乙两车先后从上海出发去南京,甲车先行50km后乙车出发,甲车每小时行80km,乙车每小时行100km。乙车要花几个小时才能追上甲车?
等量关系二:
乙车行的距离—甲车行的距离=50km
解:乙车X小时后追上甲车
100x—80x=50
x=50÷20
x=2.5
答:经过2.5小时后两车相遇。
变式三:甲、乙两车同时从上海出发去南京,甲车在距离乙车前面50km的地方出发,甲车每小时行80km,乙车每小时行100km。乙车要花几个小时才能追上甲车?
解:乙车X小时后追上甲车
等量关系一:
甲车行驶的距离=乙车行驶的距离+50km
50+80x=100x
x=50÷20
x=2.5
追及问题
答:经过2.5小时后两车相遇。
上海
南京
乙
甲
80km/h
100km/h
50km
100x
80x
等量关系二:
乙车行的距离—甲车行的距离=50km
小结二:“追及问题”
路程=速度×时间
乙
甲
a
等量关系一:
甲车行驶的距离+a=乙车行驶的距离
等量关系二:
乙车行的距离—甲车行的距离=a
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设宿舍有X间,则学生有4X人
等量关系是:
每间住4人的总人数=每间住6人的总人数
6X-30=4X
2X=30
X=15
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设宿舍有X间,则住宿的学生可以用4X表示或者6X-30表示
分配过程中的总数不变
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设宿舍有X间,则学生有4X人
等量关系是:
每间住6人的总人数-每间住4人的总人数=多出来的5间房×每个房间住6个人
6X-4X=5×6
2X=30
X=15
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设宿舍有X间,则住宿的学生可以用4X表示或者6X-30表示
分配过程中的总数不变
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设宿舍有X间,则学生有4X人
等量关系是:
每间住6人的总人数-每间住4人的总人数=多出来的5间房×每个房间住6个人
6X-4X=5×6
2X=30
X=15
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设宿舍有X间,则住宿的学生可以用4X表示或者6X-30表示
分配过程中的总数不变
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
解:设学生有X人,
则宿舍有X÷4或者(X÷6+5)间
等量关系是:
每间房间住4人的房间数=每间房间住6人的总房间数+多出来的5间房
X÷4=X÷6+5
6X=4X+5×24
X=60
宿舍:60÷4=15(间)
盈亏问题
答:宿舍有15间,学生有60人。
分配到的房间数不同,
但是参与分配的学生人数相同。
假设学生共有X人
分配过程中的总数不变
宿舍房间数可以用X÷4或者(X÷6+5)
探究三:学校给新生分配宿舍。如果每个房间仅住4人,刚好住满。如果每个房间住6人,刚好空出5个房间。宿舍有多少间?房间一共有多少人?
盈亏问题
分析
每个房间住6个人比每个房间住4个人少住了5个房间,但每次多住2个人
所以住6个人的房间数是4×5÷2=10(间)
总的房间数是10+5=15(间)
分配过程中的总数不变
新生人数是15×4=60(人)
或者(15-5)×6=60(人)
答:一共有15间宿舍,60个学生。
探究四:一盒糖平均分给几个小朋友,如果每人分6颗还剩下14颗,如果每人分8颗,那么正好分完,一共有几个小朋友?这盒糖有多少颗?
解:设一共有X个小朋友,则一共有8X颗糖
等量关系是:
分6颗糖的总人数=分8颗糖的总人数
8X=6X+14
2X=14
X=7
盈亏问题
答:一共有7个小朋友,这盒糖有56颗。
总糖数不变
假设一共有X个小朋友
分配过程中的总数不变
如果每个人分6颗,那么一共有(6X+14)颗糖
如果每个人分8颗,那么一共有8X颗糖
糖果总数:8×7=56(颗)
探究四:一盒糖平均分给几个小朋友,如果每人分6颗还剩下14颗,如果每人分8颗,那么正好分完,一共有几个小朋友?这盒糖有多少颗?
盈亏问题
分析
每次6颗糖比每次分8颗糖,最终多于下14颗,然而每次却少分了两颗
所以分糖的次数是14÷(8-6)=7(次)
分配过程中的总数不变
共有糖: 6×7+14=56(颗)
或者8×7=56(颗)
答:一共有7个小朋友,共有56颗糖
小结:
列方程解决问题的关键是什么?
找出未知量和已知量的等量关系
列方程解决问题的一般步骤是什么?
1、设未知数,用字母表示未知数,用未知数表示相关量
2、找出未知量与已知量的等量关系,列方程
3、解方程
4、验算并写出答
