人教版八年级数学下册 17.1勾股定理同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.1勾股定理同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 557.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 08:08:21 | ||
图片预览




文档简介
17.1勾股定理
一、选择题(共10题)
下列说法正确的是
A.若 ,, 是 的三个角 ,, 的对边,则
B.若 ,, 是 的三个角 ,, 的对边,则
C.若 ,, 是 的三个角 ,, 的对边,,则
D.若 ,, 是 的三个角 ,, 的对边,,则
如图,在高为 米,斜坡长为 米的楼梯台阶上铺地毯,则地毯的长度至少要
A. 米 B. 米 C. 米 D. 米
在 中,,,,则 的长为
A. B. C. D.
一架 分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端 分米.如果梯子的顶端沿墙下滑 分米,那么梯足将滑动
A. 分米 B. 分米 C. 分米 D. 分米
如图是一个三级台阶,它的每一级的长,宽,高分别为 , 和 , 和 是这个台阶的两个相对的端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为
A. B. C. D.
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 米,顶端距离地面 米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面 米,则小巷的宽度为
A. 米 B. 米 C. 米 D. 米
如图,一牧童在 处牧马,牧童家在 处,, 距河岸的距离 , 的长分别为 米和 米,且 , 两地的距离为 米,天黑前牧童从 点将马牵引到河边去饮水后再赶回家,那么牧童至少要走的距离是
A. 米 B. 米 C. 米 D. 米
直角三角形纸片的两直角边长分别为 ,,现将 按如图那样折叠,使点 与点 重合,折痕为 ,则 的长为
A. B. C. D.
如图,铁路 和公路 在点 处交汇,.公路 上 处距 点 米.如果火车行驶时,周围 米以内会受到噪音的影响.那么火车在铁路 上沿 方向以 米/秒的速度行驶时, 处受噪音影响的时间为
A. 秒 B. 秒 C. 秒 D. 秒
如图,三角形纸片 ,点 是 边上一点,连接 ,把 沿着 翻折,得到 , 与 交于点 ,连接 交 于点 .若 ,,, 的面积为 ,则点 到 的距离为
A. B. C. D.
二、填空题(共5题)
如图,一根竹子高 尺( 尺= 米),折断后竹子顶端落在离竹子底端 尺处,则折断处离地面的高度是 尺.
在 中,,,则高 的长是 .
如图,由三个正方形拼成的图形中,字母 所代表的正方形的面积是 .
在 ,,, 分别是 ,, 的对边,且 .
()若 ,,则 .
()若 ,,则 .
()若 ,,则 .
()若 ,,则 .
如图,已知正方形 的边长为 , 是边 上一点,,将 , 分别沿折痕 , 向内折叠,点 , 在点 处重合,过点 作 ,交 的延长线于 ,则线段 的长为 .
三、解答题(共5题)
如图所示,折叠长方形一边 ,点 落在 边的点 处,已知 厘米, 厘米,求 的长.
有一只小鸟在一棵高 的小树最顶端抓虫子,它的伙伴在离该树 、高 的一棵大树的最顶端发出友好的叫声,它立刻以 的速度飞向大树的顶端,那么这只小鸟至少几秒才可能到达大树最顶端和伙伴在一起?
如图,花果山上有两只猴子在一棵树 上的点 处,且 米,它们都要到 处吃东西,其中一只猴子甲沿树爬下走到离树 米处的池塘 处,另一只猴子乙先爬到树顶 处后再沿缆绳 线段滑到 处.已知两只猴子所经过的路程相等,设 为 米.
(1) 请用含有 的整式表示线段 的长为 米;
(2) 求这棵树高有多少米
如图,一个长 的梯子 ,斜靠在一竖直的墙 上,这时 的距离为 ,如果梯子的顶端 沿墙下滑 至 点.
(1) 求梯子底端 外移距离 的长度;
(2) 猜想 与 的大小关系,并证明你的结论.
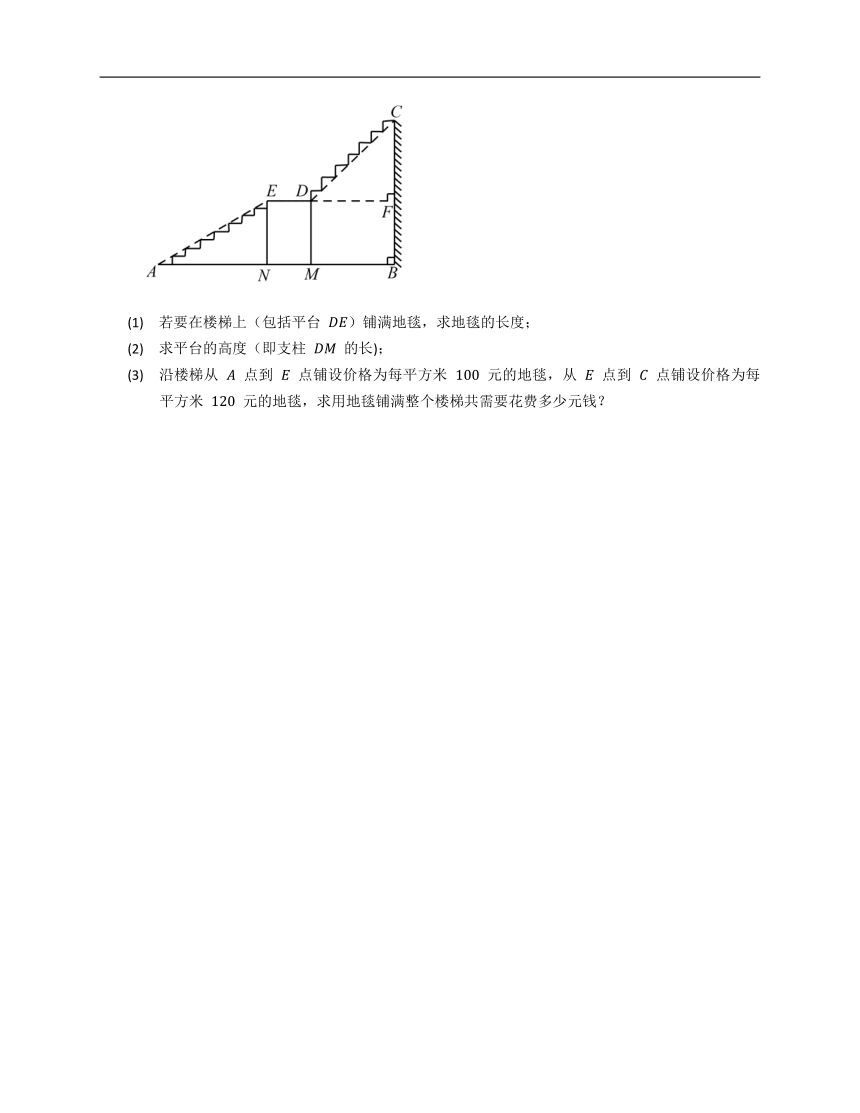
如图是某学校主楼梯从底楼到二楼的楼梯截面图,已知 米, 米,中间平台 与地面 平行,且 的长度为 米,, 为平台的两根支柱,, 垂直于 ,垂足分别为点 ,,,,楼梯宽度为 米.
(1) 若要在楼梯上(包括平台 )铺满地毯,求地毯的长度;
(2) 求平台的高度(即支柱 的长);
(3) 沿楼梯从 点到 点铺设价格为每平方米 元的地毯,从 点到 点铺设价格为每平方米 元的地毯,求用地毯铺满整个楼梯共需要花费多少元钱?
答案
一、选择题(共10题)
1. 【答案】D
2. 【答案】D
3. 【答案】C
4. 【答案】D
5. 【答案】B
【解析】展开图为:
则 ,,
在 中,.
所以蚂蚁所走的最短路线长度为 .
故选B.
6. 【答案】A
【解析】在 中,
, 米, 米,
.
在 中,
, 米,,
,
,
,
米,
米.
7. 【答案】C
【解析】如图,作点 关于 的对称点 ,连接 交 于点 ,过点 作 于点 .
由对称的性质可知,,,,
,
,,
即 为牧童要走的最短路程.
米, 米,
米.
故牧童至少要走 米.
8. 【答案】A
【解析】设 ,则 ,
,,
,
是 翻折而成,
,,
在 中,,
,解得 ,,
在 中,,
.
9. 【答案】A
【解析】如图:过点 作 , 米,
, 米,
米,
当火车到 点时对 处产生噪音影响,此时 米,
米, 米,
由勾股定理得: 米, 米,即 米,
火车在铁路 上沿 方向以 米/秒的速度行驶,
影响时间应是: 秒.
10. 【答案】B
二、填空题(共5题)
11. 【答案】
【解析】设杆子折断处离地面 尺,则斜边为 尺,
根据勾股定理得:,
解得:.
答:折断处离地面的高度是 尺.
12. 【答案】
13. 【答案】
14. 【答案】 ; ; ;
15. 【答案】
【解析】 四边形 是正方形,
,,
设 ,
在 中,
,,,
,解得 ,
,,
由翻折的性质可知,,,
,
,
,
,,
.
三、解答题(共5题)
16. 【答案】折叠长方形一边 ,
点 落在 边的点 处,
所以 厘米,
在 中,
厘米, 厘米,
由勾股定理,得:
,
,
(厘米),
(厘米).
17. 【答案】如图,抽象出数学模型.过 作 于 .
由题意可知:,.
.
在 中,.
.
答:这只小鸟至少 秒才可能到达大树顶端和伙伴在一起.
18. 【答案】
(1)
(2) ,
,
,
,
(米).
答:树高 米.
【解析】
(1) 设 为 米,且存在 ,
即 米,
米.
19. 【答案】
(1) ,,,
,
梯子的顶端 沿墙下滑 至 点,
,
,
由勾股定理得:,
.
(2) 与 的大小关系是 .
证明:连接 ,
由()知:,,
在 和 中,
,
,,
,
,
,
.
20. 【答案】
(1) 地毯的长度: 米.
(2) 设 ,
则 ,.
,
,
即 ,
,
即平台的高度为 米.
(3) 所需费用:
一、选择题(共10题)
下列说法正确的是
A.若 ,, 是 的三个角 ,, 的对边,则
B.若 ,, 是 的三个角 ,, 的对边,则
C.若 ,, 是 的三个角 ,, 的对边,,则
D.若 ,, 是 的三个角 ,, 的对边,,则
如图,在高为 米,斜坡长为 米的楼梯台阶上铺地毯,则地毯的长度至少要
A. 米 B. 米 C. 米 D. 米
在 中,,,,则 的长为
A. B. C. D.
一架 分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端 分米.如果梯子的顶端沿墙下滑 分米,那么梯足将滑动
A. 分米 B. 分米 C. 分米 D. 分米
如图是一个三级台阶,它的每一级的长,宽,高分别为 , 和 , 和 是这个台阶的两个相对的端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为
A. B. C. D.
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 米,顶端距离地面 米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面 米,则小巷的宽度为
A. 米 B. 米 C. 米 D. 米
如图,一牧童在 处牧马,牧童家在 处,, 距河岸的距离 , 的长分别为 米和 米,且 , 两地的距离为 米,天黑前牧童从 点将马牵引到河边去饮水后再赶回家,那么牧童至少要走的距离是
A. 米 B. 米 C. 米 D. 米
直角三角形纸片的两直角边长分别为 ,,现将 按如图那样折叠,使点 与点 重合,折痕为 ,则 的长为
A. B. C. D.
如图,铁路 和公路 在点 处交汇,.公路 上 处距 点 米.如果火车行驶时,周围 米以内会受到噪音的影响.那么火车在铁路 上沿 方向以 米/秒的速度行驶时, 处受噪音影响的时间为
A. 秒 B. 秒 C. 秒 D. 秒
如图,三角形纸片 ,点 是 边上一点,连接 ,把 沿着 翻折,得到 , 与 交于点 ,连接 交 于点 .若 ,,, 的面积为 ,则点 到 的距离为
A. B. C. D.
二、填空题(共5题)
如图,一根竹子高 尺( 尺= 米),折断后竹子顶端落在离竹子底端 尺处,则折断处离地面的高度是 尺.
在 中,,,则高 的长是 .
如图,由三个正方形拼成的图形中,字母 所代表的正方形的面积是 .
在 ,,, 分别是 ,, 的对边,且 .
()若 ,,则 .
()若 ,,则 .
()若 ,,则 .
()若 ,,则 .
如图,已知正方形 的边长为 , 是边 上一点,,将 , 分别沿折痕 , 向内折叠,点 , 在点 处重合,过点 作 ,交 的延长线于 ,则线段 的长为 .
三、解答题(共5题)
如图所示,折叠长方形一边 ,点 落在 边的点 处,已知 厘米, 厘米,求 的长.
有一只小鸟在一棵高 的小树最顶端抓虫子,它的伙伴在离该树 、高 的一棵大树的最顶端发出友好的叫声,它立刻以 的速度飞向大树的顶端,那么这只小鸟至少几秒才可能到达大树最顶端和伙伴在一起?
如图,花果山上有两只猴子在一棵树 上的点 处,且 米,它们都要到 处吃东西,其中一只猴子甲沿树爬下走到离树 米处的池塘 处,另一只猴子乙先爬到树顶 处后再沿缆绳 线段滑到 处.已知两只猴子所经过的路程相等,设 为 米.
(1) 请用含有 的整式表示线段 的长为 米;
(2) 求这棵树高有多少米
如图,一个长 的梯子 ,斜靠在一竖直的墙 上,这时 的距离为 ,如果梯子的顶端 沿墙下滑 至 点.
(1) 求梯子底端 外移距离 的长度;
(2) 猜想 与 的大小关系,并证明你的结论.
如图是某学校主楼梯从底楼到二楼的楼梯截面图,已知 米, 米,中间平台 与地面 平行,且 的长度为 米,, 为平台的两根支柱,, 垂直于 ,垂足分别为点 ,,,,楼梯宽度为 米.
(1) 若要在楼梯上(包括平台 )铺满地毯,求地毯的长度;
(2) 求平台的高度(即支柱 的长);
(3) 沿楼梯从 点到 点铺设价格为每平方米 元的地毯,从 点到 点铺设价格为每平方米 元的地毯,求用地毯铺满整个楼梯共需要花费多少元钱?
答案
一、选择题(共10题)
1. 【答案】D
2. 【答案】D
3. 【答案】C
4. 【答案】D
5. 【答案】B
【解析】展开图为:
则 ,,
在 中,.
所以蚂蚁所走的最短路线长度为 .
故选B.
6. 【答案】A
【解析】在 中,
, 米, 米,
.
在 中,
, 米,,
,
,
,
米,
米.
7. 【答案】C
【解析】如图,作点 关于 的对称点 ,连接 交 于点 ,过点 作 于点 .
由对称的性质可知,,,,
,
,,
即 为牧童要走的最短路程.
米, 米,
米.
故牧童至少要走 米.
8. 【答案】A
【解析】设 ,则 ,
,,
,
是 翻折而成,
,,
在 中,,
,解得 ,,
在 中,,
.
9. 【答案】A
【解析】如图:过点 作 , 米,
, 米,
米,
当火车到 点时对 处产生噪音影响,此时 米,
米, 米,
由勾股定理得: 米, 米,即 米,
火车在铁路 上沿 方向以 米/秒的速度行驶,
影响时间应是: 秒.
10. 【答案】B
二、填空题(共5题)
11. 【答案】
【解析】设杆子折断处离地面 尺,则斜边为 尺,
根据勾股定理得:,
解得:.
答:折断处离地面的高度是 尺.
12. 【答案】
13. 【答案】
14. 【答案】 ; ; ;
15. 【答案】
【解析】 四边形 是正方形,
,,
设 ,
在 中,
,,,
,解得 ,
,,
由翻折的性质可知,,,
,
,
,
,,
.
三、解答题(共5题)
16. 【答案】折叠长方形一边 ,
点 落在 边的点 处,
所以 厘米,
在 中,
厘米, 厘米,
由勾股定理,得:
,
,
(厘米),
(厘米).
17. 【答案】如图,抽象出数学模型.过 作 于 .
由题意可知:,.
.
在 中,.
.
答:这只小鸟至少 秒才可能到达大树顶端和伙伴在一起.
18. 【答案】
(1)
(2) ,
,
,
,
(米).
答:树高 米.
【解析】
(1) 设 为 米,且存在 ,
即 米,
米.
19. 【答案】
(1) ,,,
,
梯子的顶端 沿墙下滑 至 点,
,
,
由勾股定理得:,
.
(2) 与 的大小关系是 .
证明:连接 ,
由()知:,,
在 和 中,
,
,,
,
,
,
.
20. 【答案】
(1) 地毯的长度: 米.
(2) 设 ,
则 ,.
,
,
即 ,
,
即平台的高度为 米.
(3) 所需费用:
