2022-2023学年苏教版数学高一上学期假期综合复习巩固(一)(含答案)
文档属性
| 名称 | 2022-2023学年苏教版数学高一上学期假期综合复习巩固(一)(含答案) | 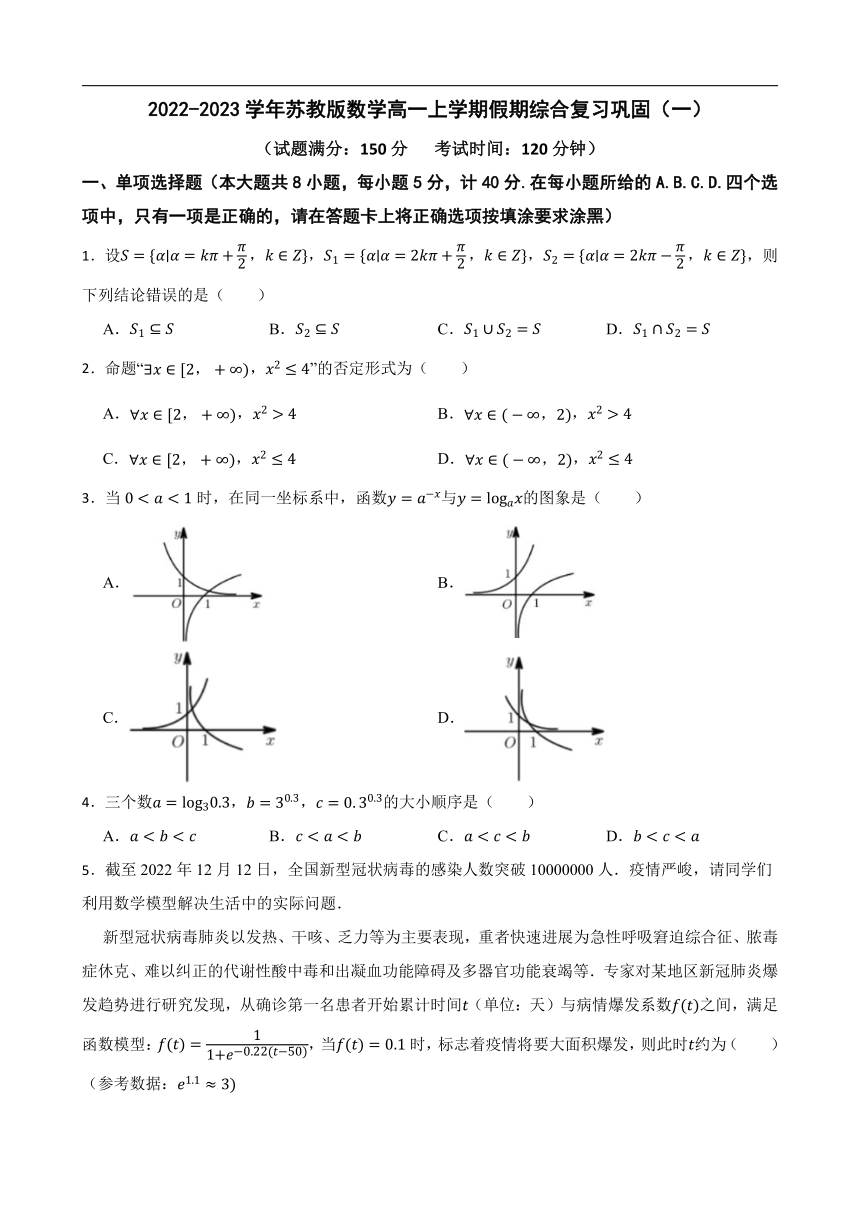 | |
| 格式 | zip | ||
| 文件大小 | 105.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-04 20:57:05 | ||
图片预览




文档简介
2022-2023学年苏教版数学高一上学期假期综合复习巩固(一)
(试题满分:150分 考试时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,计40分.在每小题所给的A.B.C.D.四个选项中,只有一项是正确的,请在答题卡上将正确选项按填涂要求涂黑)
1.设,则下列结论错误的是( )
A. B. C. D.
2.命题“,”的否定形式为( )
A., B.,
C., D.,
3.当时,在同一坐标系中,函数与的图象是( )
A. B.
C. D.
4.三个数,,的大小顺序是( )
A. B. C. D.
5.截至2022年12月12日,全国新型冠状病毒的感染人数突破10000000人.疫情严峻,请同学们利用数学模型解决生活中的实际问题.
新型冠状病毒肺炎以发热、干咳、乏力等为主要表现,重者快速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒和出凝血功能障碍及多器官功能衰竭等.专家对某地区新冠肺炎爆发趋势进行研究发现,从确诊第一名患者开始累计时间(单位:天)与病情爆发系数之间,满足函数模型:,当时,标志着疫情将要大面积爆发,则此时约为( )(参考数据:
A.38 B.40 C.45 D.47
6.函数的部分图象如图所示,则函数的解析式为( )
A. B.
C. D.
7.已知关于的不等式的解集为,其中,则的最小值为( )
A. B.1 C.2 D.8
8.已知函数,则不等式的解集为( )
A. B.
C. D.
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题所给的A.B.C.D.四个选项中,有多项是正确的,全部选对的得5分,部分选对的得2分,有选错的得0分.请在答题卡上将正确选项按填涂要求涂黑)
9.下列说法正确的是( )
A.已知集合,,若,则实数m组成的集合为
B.不等式对一切实数x恒成立的充要条件是
C.函数的最小值为2
D.“”是“”的充分不必要条件
10.已知,下列关于的说法正确的有( ).
A.为奇函数
B.的值域为
C.的解集为
D.在区间上的值域为
11.已知函数的部分图象如图所示,则下列说法正确的是( )
A.
B.函数的图象关于点对称
C.,
D.函数在上无最小值
12.已知函数是定义域为的奇函数,满足,且当时,, 则( )
A.
B.不等式的解集是
C.函数是周期函数
D.当关于的方程恰有两个不同的解时,
三、填空题(本大题共4小题,每小题5分,计20分.只要求写出最后结果,并将正确结果填写到答题卡相应位置)
13.若命题“”为假命题,则实数的取值范围是 .
14.若函数的部分图象如图所示,则此函数的解析式为 .
15.关于不等式的解集为,则关于的不等式的解集为 .
16.已知函数,若对任意实数x满足不等式,则实数a的取值范围是 .
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,请在答题卡相应位置作答)
17.在①函数的定义域为集合B,②不等式的解集为B这两个条件中任选一个,补充在下面的问题中,并解决该问题.
问题:设全集,____.
(1)当,求;
(2)若“”是“”的充分条件,求的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
18.化简求值(需要写出计算过程)
(1)若,,求的值;
(2).
19.已知函数的最大值为2,函数的图象经过点,点与它相邻的一个最低点的距离为,如图所示.
(1)求函数的解析式;
(2)若函数,当时,求函数的值域.
20.习总书记指出:“绿水青山就是金山银山.”某市一乡镇响应号召,因地制宜地将该镇打造成“生态水果特色小镇”.调研过程中发现:某珍稀水果树的单株产量W(单位:kg)与肥料费用(单位:元)满足如下关系:,其他成本投入(如培育管理等人工费)为(单位:元).已知这种水果的市场售价大约为10元/kg,且供不应求.记该单株水果树获得的利润为(单位:元).
(1)求的函数关系式;
(2)当投入的肥料费用为多少元时,该单株水果树获得的利润最大?最大利润是多少元?
21.已知是定义域为的奇函数,当时,.
(1)求的解析式;
(2)判断在上的单调性,并用定义证明.
22.已知函数的定义域为,对任意的,都有.当时,,且.
(1)求的值,并证明:当时,;
(2)判断的单调性,并证明;
(3)若,求不等式的解集.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】A,B
10.【答案】A,D
11.【答案】B,C
12.【答案】B,C
13.【答案】
14.【答案】.
15.【答案】
16.【答案】
17.【答案】(1)解:若选①,则,解得,
∴,
当时,,
∴,
∴;
若选②,则,解得,
下同选①;
(2)解:若“”是“”的充分条件,则,
∴,解得,
即的取值范围为.
18.【答案】(1)解:,,得
(2)解:原式
19.【答案】(1)解:由函数的最大值为2得.
又由其图象经过点,得.
∵图象上相邻的最高点与最低点的距离为,
,即,,所以,即.
(2)解:由函数得,
即.由,得,
所以时,;时,.
,故的值域为.
20.【答案】(1)解:为,,
所以.
(2)解:当时,,
由一元二次函数性质可知,在上单调递减,在上单调递增,
且
从而,
即在上的最大值为240;
当时,,
因为,
当且仅当,即时,不等式取等号,
从而,
即当时,有最大值270,
此时肥料费用.
综上所述,当肥料费用为30元时,该单株水果树获得的利润最大,利润最大值为270元.
21.【答案】(1)解:由题意得,当时,;
当时,.
故
(2)解:在上单调递增.
证明:由题意得,,
设,,且,
则,
由,得,得,即,
所以,即. 故在上单调递增.
22.【答案】(1)解:令,则,又,所以.
证明:当时,,所以,
又,
所以,即.
(2)解:在上单调递减.
证明如下:设,则,
又,所以,所以,
又当时,,当时,,,
所以,即,
所以在上单调递减.
(3)解:因为,所以,
所以,即,
又在上单调递减,所以,
解得,所以不等式的解集为.
(试题满分:150分 考试时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,计40分.在每小题所给的A.B.C.D.四个选项中,只有一项是正确的,请在答题卡上将正确选项按填涂要求涂黑)
1.设,则下列结论错误的是( )
A. B. C. D.
2.命题“,”的否定形式为( )
A., B.,
C., D.,
3.当时,在同一坐标系中,函数与的图象是( )
A. B.
C. D.
4.三个数,,的大小顺序是( )
A. B. C. D.
5.截至2022年12月12日,全国新型冠状病毒的感染人数突破10000000人.疫情严峻,请同学们利用数学模型解决生活中的实际问题.
新型冠状病毒肺炎以发热、干咳、乏力等为主要表现,重者快速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒和出凝血功能障碍及多器官功能衰竭等.专家对某地区新冠肺炎爆发趋势进行研究发现,从确诊第一名患者开始累计时间(单位:天)与病情爆发系数之间,满足函数模型:,当时,标志着疫情将要大面积爆发,则此时约为( )(参考数据:
A.38 B.40 C.45 D.47
6.函数的部分图象如图所示,则函数的解析式为( )
A. B.
C. D.
7.已知关于的不等式的解集为,其中,则的最小值为( )
A. B.1 C.2 D.8
8.已知函数,则不等式的解集为( )
A. B.
C. D.
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题所给的A.B.C.D.四个选项中,有多项是正确的,全部选对的得5分,部分选对的得2分,有选错的得0分.请在答题卡上将正确选项按填涂要求涂黑)
9.下列说法正确的是( )
A.已知集合,,若,则实数m组成的集合为
B.不等式对一切实数x恒成立的充要条件是
C.函数的最小值为2
D.“”是“”的充分不必要条件
10.已知,下列关于的说法正确的有( ).
A.为奇函数
B.的值域为
C.的解集为
D.在区间上的值域为
11.已知函数的部分图象如图所示,则下列说法正确的是( )
A.
B.函数的图象关于点对称
C.,
D.函数在上无最小值
12.已知函数是定义域为的奇函数,满足,且当时,, 则( )
A.
B.不等式的解集是
C.函数是周期函数
D.当关于的方程恰有两个不同的解时,
三、填空题(本大题共4小题,每小题5分,计20分.只要求写出最后结果,并将正确结果填写到答题卡相应位置)
13.若命题“”为假命题,则实数的取值范围是 .
14.若函数的部分图象如图所示,则此函数的解析式为 .
15.关于不等式的解集为,则关于的不等式的解集为 .
16.已知函数,若对任意实数x满足不等式,则实数a的取值范围是 .
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤,请在答题卡相应位置作答)
17.在①函数的定义域为集合B,②不等式的解集为B这两个条件中任选一个,补充在下面的问题中,并解决该问题.
问题:设全集,____.
(1)当,求;
(2)若“”是“”的充分条件,求的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
18.化简求值(需要写出计算过程)
(1)若,,求的值;
(2).
19.已知函数的最大值为2,函数的图象经过点,点与它相邻的一个最低点的距离为,如图所示.
(1)求函数的解析式;
(2)若函数,当时,求函数的值域.
20.习总书记指出:“绿水青山就是金山银山.”某市一乡镇响应号召,因地制宜地将该镇打造成“生态水果特色小镇”.调研过程中发现:某珍稀水果树的单株产量W(单位:kg)与肥料费用(单位:元)满足如下关系:,其他成本投入(如培育管理等人工费)为(单位:元).已知这种水果的市场售价大约为10元/kg,且供不应求.记该单株水果树获得的利润为(单位:元).
(1)求的函数关系式;
(2)当投入的肥料费用为多少元时,该单株水果树获得的利润最大?最大利润是多少元?
21.已知是定义域为的奇函数,当时,.
(1)求的解析式;
(2)判断在上的单调性,并用定义证明.
22.已知函数的定义域为,对任意的,都有.当时,,且.
(1)求的值,并证明:当时,;
(2)判断的单调性,并证明;
(3)若,求不等式的解集.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】A,B
10.【答案】A,D
11.【答案】B,C
12.【答案】B,C
13.【答案】
14.【答案】.
15.【答案】
16.【答案】
17.【答案】(1)解:若选①,则,解得,
∴,
当时,,
∴,
∴;
若选②,则,解得,
下同选①;
(2)解:若“”是“”的充分条件,则,
∴,解得,
即的取值范围为.
18.【答案】(1)解:,,得
(2)解:原式
19.【答案】(1)解:由函数的最大值为2得.
又由其图象经过点,得.
∵图象上相邻的最高点与最低点的距离为,
,即,,所以,即.
(2)解:由函数得,
即.由,得,
所以时,;时,.
,故的值域为.
20.【答案】(1)解:为,,
所以.
(2)解:当时,,
由一元二次函数性质可知,在上单调递减,在上单调递增,
且
从而,
即在上的最大值为240;
当时,,
因为,
当且仅当,即时,不等式取等号,
从而,
即当时,有最大值270,
此时肥料费用.
综上所述,当肥料费用为30元时,该单株水果树获得的利润最大,利润最大值为270元.
21.【答案】(1)解:由题意得,当时,;
当时,.
故
(2)解:在上单调递增.
证明:由题意得,,
设,,且,
则,
由,得,得,即,
所以,即. 故在上单调递增.
22.【答案】(1)解:令,则,又,所以.
证明:当时,,所以,
又,
所以,即.
(2)解:在上单调递减.
证明如下:设,则,
又,所以,所以,
又当时,,当时,,,
所以,即,
所以在上单调递减.
(3)解:因为,所以,
所以,即,
又在上单调递减,所以,
解得,所以不等式的解集为.
同课章节目录
