第六章 实数小结与复习 课件(共18张PPT)
文档属性
| 名称 | 第六章 实数小结与复习 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 09:19:33 | ||
图片预览






文档简介
(共18张PPT)
第6章小结与复习
人教版七年级下册
正
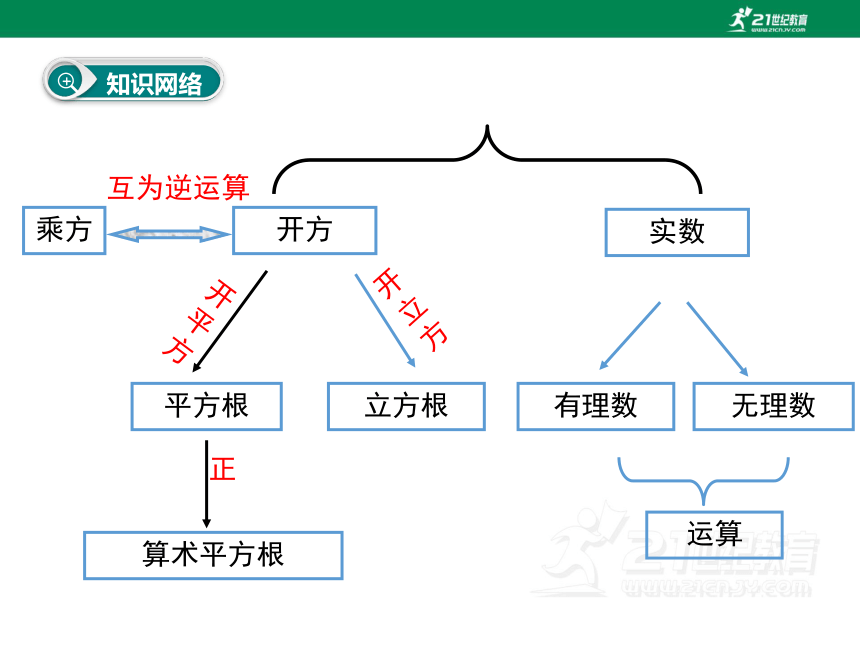
知识网络
乘方
开方
平方根
立方根
开平方
开立方
互为逆运算
算术平方根
实数
有理数
无理数
运算
专题复习
【例1】1.求下列各数的平方根:
2.求下列各数的立方根:
【归纳拓展】解题时,要注意题目的要求,是求平方根、立方根还是求算术平方根.
专题一 开方运算
【迁移应用1】求下列各式的值:
答案:① 20;② ;③ ;④ .
【例2】在-7.5, , 4, , , , 中,无理数的个数是( )
A. 1个 B. 2个 C.3个 D.4个
【归纳拓展】对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
B
专题二 实数的有关概念
【迁移应用2】(1)在- ,0.618, , , 中,
负有理数的个数是( )
A. 1个 B. 2个 C.3个 D.4个
A
A. 1个 B. 2个 C.3个 D.4个
(2)下列实数 , , ,3.14159, ,- 中,正分数的个数是( )
B
【注意】 , 等不属于分数,而是无理数.
【例3】(1) 位于整数 和 之间.
(2)实数a,b在数轴上的位置如图所示,化简
= .
a
0
b
-2a
【归纳拓展】
1.实数与数轴上的点是一一对应的关系;
2.在数轴上表示的数,右边的数总是比左边的数大.
专题三 实数的估算及与数轴的结合
4
5
【迁移应用3】如图所示,数轴上与1, 对应的点分别是为A、B,点B关于点A的对称点为C,设点C表示的数为x,则
= .
0
1
2
B
C
A
【例4】(1) (2)
60
y-1
【例5】已知 , ,
,则 = , = .
0.08138
37.77
【例6】计算: = .
专题四 实数的运算
【归纳拓展】开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
【迁移应用4】计算:
答案:(1)5.79;(2)5.48
课堂小结
1.通过对本章内容的复习,你认为平方根和立方根之
间有怎么样的区别与联系?
2.什么是实数?
3.实数的运算法则与有理数的运算法则有什么联系?
课后训练
1.写出两个大于1小于4的无理数____、____.
2. 的整数部分为____,小数部分为_ ____.
3.一个立方体的棱长是4cm,如果把它体积扩大为
原来的8倍,则扩大后的立方体的表面积是_______.
3
4.求下列各式中的x.
(1) (x-1)2=64; (2)
(x=9或-7 )
(x=-18)
5.比较大小: 与 .
解:∵(-2+ )-(-2+ )= -2+ +2- = - >0
∴-2+ >-2+
另解:直接由正负决定-2+ >-2+
6.若
求-ab 的平方根.
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a= ,b= .
∴-ab=-( × )=1 ,
∴ 1 的平方根是±1.
7.计算:
解:原式=3.6;
解:原式=-4.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第6章小结与复习
人教版七年级下册
正
知识网络
乘方
开方
平方根
立方根
开平方
开立方
互为逆运算
算术平方根
实数
有理数
无理数
运算
专题复习
【例1】1.求下列各数的平方根:
2.求下列各数的立方根:
【归纳拓展】解题时,要注意题目的要求,是求平方根、立方根还是求算术平方根.
专题一 开方运算
【迁移应用1】求下列各式的值:
答案:① 20;② ;③ ;④ .
【例2】在-7.5, , 4, , , , 中,无理数的个数是( )
A. 1个 B. 2个 C.3个 D.4个
【归纳拓展】对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
B
专题二 实数的有关概念
【迁移应用2】(1)在- ,0.618, , , 中,
负有理数的个数是( )
A. 1个 B. 2个 C.3个 D.4个
A
A. 1个 B. 2个 C.3个 D.4个
(2)下列实数 , , ,3.14159, ,- 中,正分数的个数是( )
B
【注意】 , 等不属于分数,而是无理数.
【例3】(1) 位于整数 和 之间.
(2)实数a,b在数轴上的位置如图所示,化简
= .
a
0
b
-2a
【归纳拓展】
1.实数与数轴上的点是一一对应的关系;
2.在数轴上表示的数,右边的数总是比左边的数大.
专题三 实数的估算及与数轴的结合
4
5
【迁移应用3】如图所示,数轴上与1, 对应的点分别是为A、B,点B关于点A的对称点为C,设点C表示的数为x,则
= .
0
1
2
B
C
A
【例4】(1) (2)
60
y-1
【例5】已知 , ,
,则 = , = .
0.08138
37.77
【例6】计算: = .
专题四 实数的运算
【归纳拓展】开立方运算时要注意小数点的变化规律,开立方是三位与一位的关系,开平方是二位与一位的关系.
【迁移应用4】计算:
答案:(1)5.79;(2)5.48
课堂小结
1.通过对本章内容的复习,你认为平方根和立方根之
间有怎么样的区别与联系?
2.什么是实数?
3.实数的运算法则与有理数的运算法则有什么联系?
课后训练
1.写出两个大于1小于4的无理数____、____.
2. 的整数部分为____,小数部分为_ ____.
3.一个立方体的棱长是4cm,如果把它体积扩大为
原来的8倍,则扩大后的立方体的表面积是_______.
3
4.求下列各式中的x.
(1) (x-1)2=64; (2)
(x=9或-7 )
(x=-18)
5.比较大小: 与 .
解:∵(-2+ )-(-2+ )= -2+ +2- = - >0
∴-2+ >-2+
另解:直接由正负决定-2+ >-2+
6.若
求-ab 的平方根.
解:∵|3a+4|≥0且(4b-3)2≥0
而|3a+4|+(4b-3)2=0
∴|3a+4|=0且(4b-3)2=0
∴a= ,b= .
∴-ab=-( × )=1 ,
∴ 1 的平方根是±1.
7.计算:
解:原式=3.6;
解:原式=-4.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
