数学人教A版（2019）选择性必修第二册4.3.2等比数列的前n项和公式（共45张ppt）

(共45张PPT)
第四章 数列
4.3.2等比数列的前n项和公式
第一课时
一
二
三
学习目标
理解等比数列的前n项和公式的推导方法
握等比数列的n项和公式并能运用公式解决一些简单问题
提高学生的建模意识，体会公式探求过程中从特殊到一般的思维方法，渗透方程思想、分类讨论思想
学习目标
复习回顾
回顾1 等比数列的定义与递推公式是怎样的？
一般地，如果一个数列从第 2 项起，每一项与它的前一项的比都等于同一个常数, 那么这个数列叫做等比数列,这个常数叫做等比数列的公比，公比通常用字母表示(显然)．
等比数列的递推关系：
或
回顾2 等比数列的通项公式是什么？
首项为,公比为的等比数列的通项公式为
（n∈N﹡, q≠0）
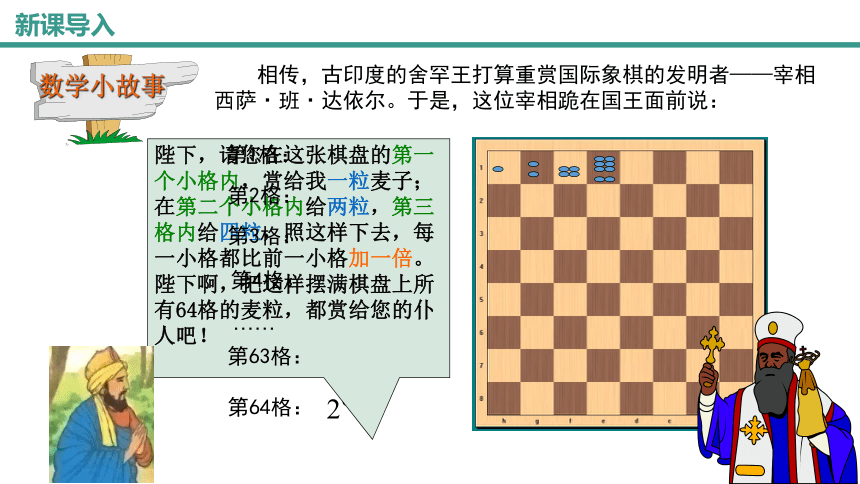
数学小故事
相传，古印度的舍罕王打算重赏国际象棋的发明者——宰相西萨·班·达依尔。于是，这位宰相跪在国王面前说：
新课导入
1
2
陛下，请您在这张棋盘的第一个小格内，赏给我一粒麦子；在第二个小格内给两粒，第三格内给四粒，照这样下去，每一小格都比前一小格加一倍。
陛下啊，把这样摆满棋盘上所
有64格的麦粒，都赏给您的仆人吧！
第1格：
第2格：
第4格：
第3格：
第63格：
第64格：
……
新知探究一：等比数列的前n项和公式的推导与公式
问题1：这位聪明的宰相到底要求的是多少麦粒呢？
麦粒总数为
追问1： 构成什么数列？
等比数列
追问2： 应归结为什么数学问题呢？
求等比数列的前n项和问题
①式两边同乘以2则有
2S64=2+22+23+···+263+264 ②
追问3：观察相邻两项的特征，有何联系？
如果我们把每一项都乘以2，
就变成了与它相邻的
后一项
S64=1+2+22+···+ 262 +263 ①
新知探究一：等比数列的前n项和公式的推导与公式
①
②
反思：纵观全过程，①式两边为什么要乘以2 ？
乘以3？
会达到一样的效果吗？
追问4：比较①、②两式，你有什么发现？
新知探究一：等比数列的前n项和公式的推导与公式
①-②得：
错位相减法
①
②
①-②得：
①×q 得
问题2：类比上面求和的方法能否得到等比数列前n项和公式呢？
新知探究一：等比数列的前n项和公式的推导与公式
思考：要求出Sn,是否可以把上式两边同除以（1-q）？
注意：分类讨论是一种常用的数学思想方法！
新知探究一：等比数列的前n项和公式的推导与公式
首项
末项
公比
前n项和
项数
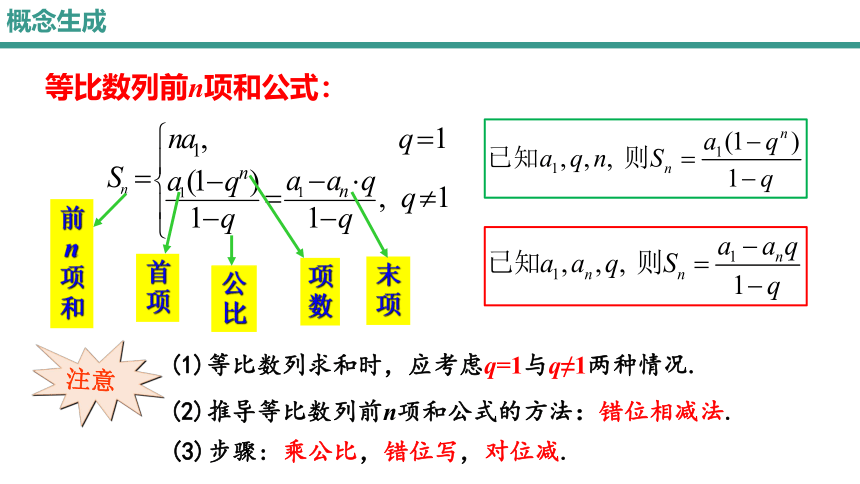
等比数列前n项和公式：
注意
(1)等比数列求和时，应考虑q=1与q≠1两种情况.
(2)推导等比数列前n项和公式的方法：错位相减法.
(3)步骤: 乘公比，错位写，对位减.
概念生成
1000粒麦子的质量约为40g
麦粒的总质量超过了7000亿吨
呼应故事
是2016~2017年世界小麦年产量（7亿多吨）的981倍，按每年7亿吨计算都要用1000多年才能满足西萨的要求；如果按人均每天吃______粮食计算,此棋盘上的粮食可供全世界_____亿人吃上约_____年.
1千克
80
240
所以国王兑现不了他的承诺。
跟踪练习：判断是非
2
n
n个
5n
公式辨析
n
且
0 a=0
n a=1
{
=
反思总结:
用公式前，先弄清楚数列的首项 、公比 、项数n
公式辨析
新知探究二：等比数列的前n项和公式的应用
新知探究二：等比数列的前n项和公式的应用
例7 已知数列{an}是等比数列.
1. 已知数列{an}是等比数列.
课本P37
1. 已知数列{an}是等比数列.
课本P37
新知探究二：等比数列的前n项和公式的应用
例2 已知等比数列{an}的首项为－1，前n项和为Sn，若 求公比q.
课本P37
4. 已知三个数成等比数列，它们的和等于14，积等于64. 求这个等比数列的首项和公比.
课本P37
5. 如果一个等比数列前5项的和等于10，前10项的和等于50，那么这个数列的公比等于多少
课本P37
解法1：
例3
(1)
(2)
(3)
解法2：
两式相除：实现整体消元的目的
新知探究二：等比数列的前n项和公式的应用
例4 已知等比数列{an}的公比q ≠ －1，前n项和为Sn，证明 Sn , S2n－Sn , S3n－S2n , 成等比数列，并这个数列的公比.
新知探究二：等比数列的前n项和公式的应用
例4 已知等比数列{an}的公比q ≠ －1，前n项和为Sn，证明 Sn , S2n－Sn , S3n－S2n , 成等比数列，并这个数列的公比.
新知探究二：等比数列的前n项和公式的应用
若等比数列{an}的公比q≠－1，前n项和为Sn，则Sn, S2n－Sn, S3n－S2n成等比数列,其中公比为qn.
等比数列的片段和性质：
1.掌握等比数列前n项和公式推导方法（错位相减法）.
2.掌握等比数列前n项和公式（注意分类讨论）.
课堂小结
第四章 数列
4.3.2等比数列的前n项和公式
第二课时
一
二
三
学习目标
能在具体的问题情境中，发现数列的等比关系，并解决相应的问题
理解等比数列前项和公式的性质
应用等比数列前项和公式的性质解题
学习目标
新知探究一：等比数列的前n项和公式的实际应用
例10 如图，正方形ABCD的边长为5cm，取正方形ABCD各边的中点E, F, G, H，作第2个正方形EFGH，然后再取正方形EFGH各边的中点I, J, K, L，作第3个正方形IJKL，依此方法一直继续下去.
(1) 求从正方形ABCD开始，连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去，那么所有这些正方形的面积之和将趋近于多少
分析：可以利用数列表示各正方形的面积，根据条件可知，这是一个等比数列.
解:设各个正方形的面积组成数列{an}，正方形ABCD的面积为首项a1 , 则a1=25
29
新知探究一：等比数列的前n项和公式的实际应用
1. 一个乒乓球从1 m高的高度自由落下，每次落下后反弹的高度都是原来高度的0.61倍.
(1) 当它第6次着地时，经过的总路程是多少(精确到1 cm)
(2) 至少在第几次着地后，它经过的总路程能达到400 cm
课本P40
新知探究一：等比数列的前n项和公式的实际应用
例11 去年某地产生的生活垃圾为20万吨，其中14万吨垃圾以填埋方式处理，6万吨垃圾以环保方式处理，预计每年生活垃圾的总量递增5%，同时，通过环保方式处理的垃圾量每年增加1.5万吨. 为了确定处理生活垃圾的预算，请写出从今年起n年内通过填埋方式处理的垃圾总量的计算公式，并计算从今年起5年内通过填埋方式处理的垃圾总量 (精确到0.1万吨).
分析：由题意可知，每年生活垃圾的总量构成等比数列,而每年以环保方式处理的垃圾量构成等差数列 . 因此 ,可以利用等差数列、等比数列的知识进行计算.
解: 设从今年起每年生活垃圾的总量(单位:万吨)构成数列{an}，每年以环保方式处理的垃圾量(单位:万吨)构成数列{bn}，n年内通过填埋方式处理的垃圾总量为Sn(单位:万吨)，则
新知探究一：等比数列的前n项和公式的实际应用
= 20 ( 1.05+1.052+…+1.05n ) -( 7.5+9+…+6+1.5n )
常用数列求和方法之分组求和法
(1)求形如cn＝an±bn的前n项和公式，其中{an}与{bn}是等差数列或等比数列；
(2) 将等差数列和等比数列分开：
Tn＝ c1 + c2 +… + cn ＝ (a1 + a2 +… + an )± (b1 + b2 +… + bn )
(3) 利用等差数列和等比数列前n项和公式来计算Tn.
解：
变式：
例题小结
例12 某牧场今年初牛的存栏数为1200，预计以后每年存栏数的增长率为8%，且在每年年底卖出100头牛，设牧场从今年起每年年初的计划存栏数依次为c1，c2，c3， .
(1)写出一个递推公式，表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1－k = r(cn－k)的形式，其中k，r为常数;
(3) 求S10= c1＋c2＋c3＋ ＋c10的值(精确到1).
新知探究一：等比数列的前n项和公式的实际应用
分析:
(1)可以利用每年存栏数的增长率为8%和每年年底卖出100头建立cn+1与cn的关系；
(2)这是待定系数法的应用，可以将它还原为(1)中的递推公式形式, 通过比较系数,得到方程组；
(3)利用(2)的结论可得出解答.
例12 某牧场今年初牛的存栏数为1200，预计以后每年存栏数的增长率为8%，且在每年年底卖出100头牛，设牧场从今年起每年年初的计划存栏数依次为c1，c2，c3， .
(1)写出一个递推公式，表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1－k = r(cn－k)的形式，其中k，r为常数;
(3) 求S10= c1＋c2＋c3＋ ＋c10的值(精确到1).
新知探究一：等比数列的前n项和公式的实际应用
例12 某牧场今年初牛的存栏数为1200，预计以后每年存栏数的增长率为8%，且在每年年底卖出100头牛，设牧场从今年起每年年初的计划存栏数依次为c1，c2，c3， .
(1)写出一个递推公式，表示cn+1与cn之间的关系;
(2) 将(1)中的递推公式表示成cn+1－k = r(cn－k)的形式，其中k，r为常数;
(3) 求S10= c1＋c2＋c3＋ ＋c10的值(精确到1).
新知探究一：等比数列的前n项和公式的实际应用
37
课本P40
新知探究二：等比数列的前n项和公式的性质
思考：你能发现等比数列前n项和公式Sn＝ (q≠1)的函数特征吗？


当q≠1时，
即Sn是n的指数型函数.
当q＝1时，Sn＝na1，即Sn是n的正比例函数.
结构特点：qn的系数与常数项互为相反数.
【例】 数列{an}的前n项和Sn＝3n－2.求{an}的通项公式, 并判断{an}是否是等比数列.
解: 当n≥2时，an＝Sn－Sn－1＝(3n－2)－(3n－1－2)＝2·3n－1.
当n＝1时，a1＝S1＝31－2＝1，不满足上式.
由于a1＝1，a2＝6，a3＝18，
所以a1，a2，a3不是等比数列，即{an}不是等比数列.
思考：还有其他方法判断{an}是否是等比数列吗？
新知探究二：等比数列的前n项和公式的性质
探究点三 等比数列的判断及其前n项和的函数特征
精讲精练
例3 一个等比数列的前 项和 ，则 ( @16@ )
A. B. C. D.
B
[解析] 设等比数列 的公比为 ，
当 时， ，
则 ，显然与题设不符， ，即此等比数列不是常数列，
，
则 可得 ．
例4 已知数列 的前 项和为 ，若 ，判断 是不是等比数列，说明理由.
[解析] 由 ，得 ，
当 时， ,
令 ,得 ,所以 ， ，
， ， ,所以 是等比数列.
思考：若{an}是公比为q的等比数列，S偶, S奇分别是数列的偶数项和与奇数项和，则S偶, S奇之间有什么关系？
(1)若等比数列{an}的项数有2n项，则
(2)若等比数列{an}的项数有2n＋1项，则
S奇＝a1＋a3＋… ＋ a2n-1 ＋a2n+1
＝a1＋(a3＋… a2n-1 ＋a2n+1)
＝a1＋q(a2＋a4＋…＋a2n)
＝a1＋qS偶
S奇＝a1＋qS偶
S偶＝a2＋a4＋…＋a2n
S奇＝a1＋a3＋…＋a2n－1
S偶＝a2＋a4＋…＋a2n


S偶＝qS奇


新知探究二：等比数列的前n项和公式的性质
【例】 已知等比数列{an}共有2n项，其和为－240，且(a1＋a3＋…＋a2n－1)－(a2＋a4＋…＋a2n)＝80，求公比q.
解：由题意知S奇＋S偶＝－240，S奇－S偶＝80
∴S奇＝－80，S偶＝－160，
新知探究二：等比数列的前n项和公式的性质
例2 已知等比数列 共有32项，其公比 ，且奇数项之和比偶数项之和少60，则数列 的所有项之和是( @3@ )
A. B. C. D.
D
[解析] 设等比数列 的奇数项之和为 ，偶数项之和为 ,
则
又 m> ，则 ， 解得 , ，
故数列 的所有项之和是 .
1、等比数列前n项和公式，对于公比未知的等比数列，
应用等比数列的前n项和公式时，需讨论公比是否为1；
3、数学思想方法的应用:
①方程思想:等比数列求和问题中的“知三求二”问题
就是方程思想的重要体现；
②分类讨论思想：由等比数列前 项和公式可知，解答等
比数列求和问 题时常常要用到分类讨论思想.
2、等比数列前n项和公式的推导：错位相减法；
归纳小结：
45