总复习四则混合运算整理与复习(课件)-六年级下册数学苏教版(共23张PPT)
文档属性
| 名称 | 总复习四则混合运算整理与复习(课件)-六年级下册数学苏教版(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 351.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-04 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
四则混合运算整理与复习(2)
数学小讲师
数学小讲师
先观察前两题的计算过程,再照样子计算后三题。
9 × 9-1 = 9 ×(10-1)-1 = 9 ×10-9-1 = 80
98 × 9 -2 = 98 ×(10- 1)-2 = 980-98-2 = 880
987 × 9 -3 =
9876 × 9 -4 =
987 ×(10- 1)-3 = 9870-987-3 = 8880
9876 ×(10- 1)-4= 98760-9876-4= 88880
乘法分配律
减法的性质
数学小讲师
98765 × 9 -5 =
98765×(10- 1)-5 = 987650-98765-5 = 888880
987654321×9 -9 =
?
9个8
8888888880
你做对了吗?
预习单:
1.复习分数和百分数实际问题的数量关系和解题思路,并说一说如何确定单位“1”的量,列数量关系式。
2.预习六下数学书第77页内容。思考:
怎样求一个数比另一个数多(少)几分之几?
怎样求一个数比另一个数多(少)百分之几的实际问题?
3.用思维导图整理。
整理与反思
小组交流预习成果:
提 出 问 题
(1)组长进行合理分工和安排。
小组交流思维导图:
(2)小组成员按顺序进行组内发言和知识点梳理。
(3)用红笔对自己的思维导图进行补充和完善。
本节课你想从哪几个方面进行复习?
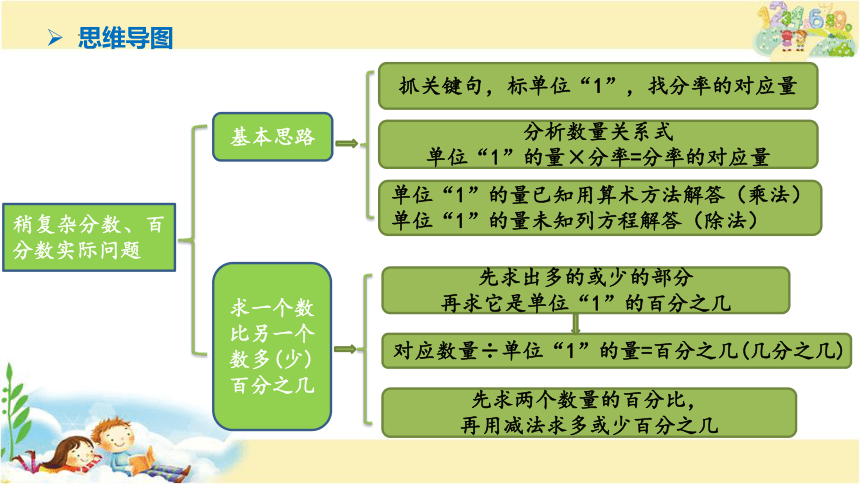
思维导图
稍复杂分数、百分数实际问题
基本思路
求一个数比另一个数多(少)百分之几
抓关键句,标单位“1”,找分率的对应量
分析数量关系式
单位“1”的量×分率=分率的对应量
单位“1”的量已知用算术方法解答(乘法)
单位“1”的量未知列方程解答(除法)
对应数量÷单位“1”的量=百分之几(几分之几)
先求两个数量的百分比,
再用减法求多或少百分之几
先求出多的或少的部分
再求它是单位“1”的百分之几
1.根据下列问题找出单位“1”的量,并说出数量关系。
(1)实际造林面积相当于原计划的百分之几?
( 实际造林面积)÷( 原计划造林面积)=实际造林面积相当于原计划的百分之几
(2)实际造林面积比原计划多百分之几?
实际造林面积比原计划多的占原计划的百分之几
基本练习
(实际比原计划多的造林面积)÷(原计划造林面积)=实际造林面积比原计划多百分之几
(1)故事书是文艺书的 。
(2)故事书比文艺书少25%。
× 25% =
文艺书的本数
故事书比文艺书少的本数
2.根据条件找出单位“1”的量,并说出数量关系式。
基本练习
文艺书的本数
故事书的本数
文艺书的本数-故事书比文艺书少的本数=故事书的本数
单位“1”的量×分数(百分数)=对应数量
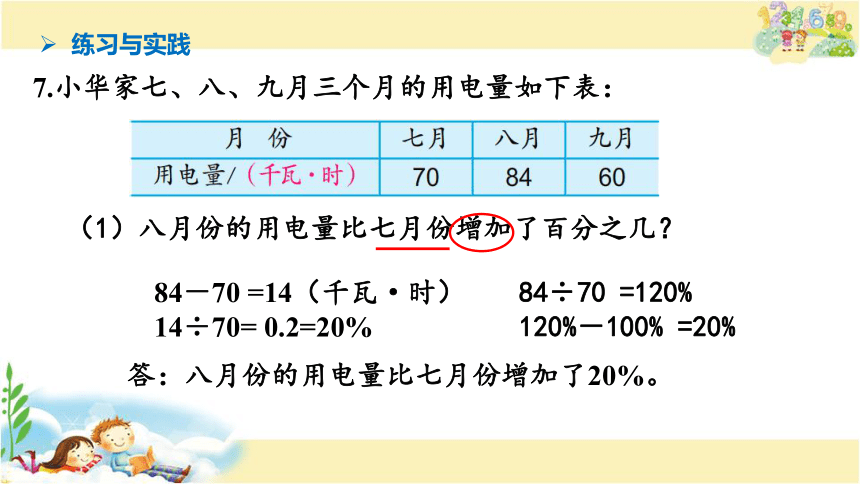
7.小华家七、八、九月三个月的用电量如下表:
(1)八月份的用电量比七月份增加了百分之几?
84-70 =14(千瓦·时)
14÷70= 0.2=20%
84÷70 =120%
120%-100% =20%
答:八月份的用电量比七月份增加了20%。
练习与实践
(2)九月份的用电量比七月份节约了百分之几?
70-60 =10(千瓦·时)
10÷70 ≈ 0.143=14.3%
60÷70 ≈ 0.857=85.7%
100%-85.7% =14.3%
答:九月份的用电量比七月份节约了14.3%,比八月份大约节约了28.6%。
84-60 =24(千瓦·时)
24÷84 ≈ 0.286=28.6%
60÷84 ≈ 0.714=71.4%
100%-71.4% =28.6%
比八月份呢?
练习与实践
8.某商场有奖销售活动设置了10000 张奖券,其中一、 二、 三等奖的中奖率分别是5%、10%和30%。
(1) 一等奖和二等奖的奖券一共有多少张?
10000×5%=500(张)10000×10%=1000(张)
500+1000=1500(张)
答:一等奖和二等奖的奖券一共有1500张。
(2)你还能提出什么问题?
练习与实践
一等奖比二等奖的奖券少百分之几?
(1000 - 500)÷1000=0.5=50%
思考:一等奖比二等奖的奖券少50%,可以说二等奖比一等奖的奖券多50%吗?为什么?
答:一等奖比二等奖的奖券少50%。
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
练习与实践
(63-56) ÷ 56
=7÷56
=
答:美术组的人数比舞蹈组多 。
(2)三信小学美术组有63 人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
(3)三信小学美术组有63人,比舞蹈组的人多 。舞蹈组有多少人?
已知
未知
练习与实践
算数方法解答
列方程解答
(1)找出单位“1”
(2)分析数量关系式
(3)观察这两题相同和不同之处
(4)小组汇报
活动要求:
答:舞蹈组有56人。
(2)三信小学美术组有63人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
= 63 - 7
= 56(人)
美术组的人数- 舞蹈组比美术组少的人数 = 舞蹈组的人数
练习与实践
63-63×
(3)三信小学美术组有63人,比舞蹈组的人数多 。舞蹈组有多少人?
答:舞蹈组有56人。
舞蹈组的人数+美术组比舞蹈组多的人数=美术组的人数
练习与实践
解:设舞蹈组有x人。
x+ x = 63
x = 63
x = 56
练习与实践
10.(1)一袋大米,先用去 ,又用去 ,两次一共用去6千克。这袋大米原来有多少千克?
(2)一袋大米,先用去 ,又用去 千克,两次一共用去 千克。这袋大米原来有多少千克?
活动要求:
(1)找出单位“1”的量。
(2)分析数量关系式。
(3)观察这两题相同和不同之处。
(4)小组汇报。
10.(1)一袋大米,先用去 ,又用去 ,两次一共用去6千克。这袋大米原来有多少千克?
答:这袋大米原来有10千克。
6千克
?千克
先用去的质量+又用去的质量=两次一共用去的质量
练习与实践
x = 10
x = 6
解:设这袋大米原来有x千克。
+ x = 6
x
6千克
答:这袋大米原来有10千克。
10.(2)一袋大米,先用去 ,又用去 千克,两次一共用去
千克。这袋大米原来有多少千克?
千克
?千克
先用去的质量+又用去的质量=两次一共用去的
练习与实践
解:设这袋大米原来有 x千克。
x + =
x = 10
x = 2
对比观察
10.(1)一袋大米,先用去 ,又用去 ,两次一共用去6千克。这袋大米原来有多少千克?
x = 10
x = 6
解:设这袋大米原来有x千克。
+ x = 6
x
答:这袋大米原来有10千克。
10.(2)一袋大米,先用去 ,又用去 千克,两次一共用去千克。这袋大米原来有多少千克?
先用去的+又用去的=两次一共用去的
先用去的+又用去的=两次一共用去的
解:设这袋大米原来有x千克。
x + =
x = 10
x = 2
答:这袋大米原来有10千克。
分析数量关系
列式解答
回顾反思
理解题意
课堂总结
思维冲浪
1.有两根同样长的绳子,第一根用去 米,第二根用去 ,如果第一根剩下的长,那么这两根绳子原来的长度与1米相比,( )。
A.比1米长 B.比1米短 C.一样长 D.无法确定
A
同学们回顾一下,这节课我们复习了哪些内容?你有什么收获和体会?
回 顾 反 思
布置作业
预习书78-79页“整理与反思”、“练习与实践”第1-5题。
四则混合运算整理与复习(2)
数学小讲师
数学小讲师
先观察前两题的计算过程,再照样子计算后三题。
9 × 9-1 = 9 ×(10-1)-1 = 9 ×10-9-1 = 80
98 × 9 -2 = 98 ×(10- 1)-2 = 980-98-2 = 880
987 × 9 -3 =
9876 × 9 -4 =
987 ×(10- 1)-3 = 9870-987-3 = 8880
9876 ×(10- 1)-4= 98760-9876-4= 88880
乘法分配律
减法的性质
数学小讲师
98765 × 9 -5 =
98765×(10- 1)-5 = 987650-98765-5 = 888880
987654321×9 -9 =
?
9个8
8888888880
你做对了吗?
预习单:
1.复习分数和百分数实际问题的数量关系和解题思路,并说一说如何确定单位“1”的量,列数量关系式。
2.预习六下数学书第77页内容。思考:
怎样求一个数比另一个数多(少)几分之几?
怎样求一个数比另一个数多(少)百分之几的实际问题?
3.用思维导图整理。
整理与反思
小组交流预习成果:
提 出 问 题
(1)组长进行合理分工和安排。
小组交流思维导图:
(2)小组成员按顺序进行组内发言和知识点梳理。
(3)用红笔对自己的思维导图进行补充和完善。
本节课你想从哪几个方面进行复习?
思维导图
稍复杂分数、百分数实际问题
基本思路
求一个数比另一个数多(少)百分之几
抓关键句,标单位“1”,找分率的对应量
分析数量关系式
单位“1”的量×分率=分率的对应量
单位“1”的量已知用算术方法解答(乘法)
单位“1”的量未知列方程解答(除法)
对应数量÷单位“1”的量=百分之几(几分之几)
先求两个数量的百分比,
再用减法求多或少百分之几
先求出多的或少的部分
再求它是单位“1”的百分之几
1.根据下列问题找出单位“1”的量,并说出数量关系。
(1)实际造林面积相当于原计划的百分之几?
( 实际造林面积)÷( 原计划造林面积)=实际造林面积相当于原计划的百分之几
(2)实际造林面积比原计划多百分之几?
实际造林面积比原计划多的占原计划的百分之几
基本练习
(实际比原计划多的造林面积)÷(原计划造林面积)=实际造林面积比原计划多百分之几
(1)故事书是文艺书的 。
(2)故事书比文艺书少25%。
× 25% =
文艺书的本数
故事书比文艺书少的本数
2.根据条件找出单位“1”的量,并说出数量关系式。
基本练习
文艺书的本数
故事书的本数
文艺书的本数-故事书比文艺书少的本数=故事书的本数
单位“1”的量×分数(百分数)=对应数量
7.小华家七、八、九月三个月的用电量如下表:
(1)八月份的用电量比七月份增加了百分之几?
84-70 =14(千瓦·时)
14÷70= 0.2=20%
84÷70 =120%
120%-100% =20%
答:八月份的用电量比七月份增加了20%。
练习与实践
(2)九月份的用电量比七月份节约了百分之几?
70-60 =10(千瓦·时)
10÷70 ≈ 0.143=14.3%
60÷70 ≈ 0.857=85.7%
100%-85.7% =14.3%
答:九月份的用电量比七月份节约了14.3%,比八月份大约节约了28.6%。
84-60 =24(千瓦·时)
24÷84 ≈ 0.286=28.6%
60÷84 ≈ 0.714=71.4%
100%-71.4% =28.6%
比八月份呢?
练习与实践
8.某商场有奖销售活动设置了10000 张奖券,其中一、 二、 三等奖的中奖率分别是5%、10%和30%。
(1) 一等奖和二等奖的奖券一共有多少张?
10000×5%=500(张)10000×10%=1000(张)
500+1000=1500(张)
答:一等奖和二等奖的奖券一共有1500张。
(2)你还能提出什么问题?
练习与实践
一等奖比二等奖的奖券少百分之几?
(1000 - 500)÷1000=0.5=50%
思考:一等奖比二等奖的奖券少50%,可以说二等奖比一等奖的奖券多50%吗?为什么?
答:一等奖比二等奖的奖券少50%。
9.(1)三信小学美术组有63人,舞蹈组有56人。美术组的人数比舞蹈组多几分之几?
练习与实践
(63-56) ÷ 56
=7÷56
=
答:美术组的人数比舞蹈组多 。
(2)三信小学美术组有63 人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
(3)三信小学美术组有63人,比舞蹈组的人多 。舞蹈组有多少人?
已知
未知
练习与实践
算数方法解答
列方程解答
(1)找出单位“1”
(2)分析数量关系式
(3)观察这两题相同和不同之处
(4)小组汇报
活动要求:
答:舞蹈组有56人。
(2)三信小学美术组有63人,舞蹈组的人数比美术组少 。舞蹈组有多少人?
= 63 - 7
= 56(人)
美术组的人数- 舞蹈组比美术组少的人数 = 舞蹈组的人数
练习与实践
63-63×
(3)三信小学美术组有63人,比舞蹈组的人数多 。舞蹈组有多少人?
答:舞蹈组有56人。
舞蹈组的人数+美术组比舞蹈组多的人数=美术组的人数
练习与实践
解:设舞蹈组有x人。
x+ x = 63
x = 63
x = 56
练习与实践
10.(1)一袋大米,先用去 ,又用去 ,两次一共用去6千克。这袋大米原来有多少千克?
(2)一袋大米,先用去 ,又用去 千克,两次一共用去 千克。这袋大米原来有多少千克?
活动要求:
(1)找出单位“1”的量。
(2)分析数量关系式。
(3)观察这两题相同和不同之处。
(4)小组汇报。
10.(1)一袋大米,先用去 ,又用去 ,两次一共用去6千克。这袋大米原来有多少千克?
答:这袋大米原来有10千克。
6千克
?千克
先用去的质量+又用去的质量=两次一共用去的质量
练习与实践
x = 10
x = 6
解:设这袋大米原来有x千克。
+ x = 6
x
6千克
答:这袋大米原来有10千克。
10.(2)一袋大米,先用去 ,又用去 千克,两次一共用去
千克。这袋大米原来有多少千克?
千克
?千克
先用去的质量+又用去的质量=两次一共用去的
练习与实践
解:设这袋大米原来有 x千克。
x + =
x = 10
x = 2
对比观察
10.(1)一袋大米,先用去 ,又用去 ,两次一共用去6千克。这袋大米原来有多少千克?
x = 10
x = 6
解:设这袋大米原来有x千克。
+ x = 6
x
答:这袋大米原来有10千克。
10.(2)一袋大米,先用去 ,又用去 千克,两次一共用去千克。这袋大米原来有多少千克?
先用去的+又用去的=两次一共用去的
先用去的+又用去的=两次一共用去的
解:设这袋大米原来有x千克。
x + =
x = 10
x = 2
答:这袋大米原来有10千克。
分析数量关系
列式解答
回顾反思
理解题意
课堂总结
思维冲浪
1.有两根同样长的绳子,第一根用去 米,第二根用去 ,如果第一根剩下的长,那么这两根绳子原来的长度与1米相比,( )。
A.比1米长 B.比1米短 C.一样长 D.无法确定
A
同学们回顾一下,这节课我们复习了哪些内容?你有什么收获和体会?
回 顾 反 思
布置作业
预习书78-79页“整理与反思”、“练习与实践”第1-5题。
