第七章 平面直角坐标系小结与复习 课件(共15张PPT)
文档属性
| 名称 | 第七章 平面直角坐标系小结与复习 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 09:34:33 | ||
图片预览





文档简介
(共15张PPT)
第7章小结与复习
人教版七年级下册
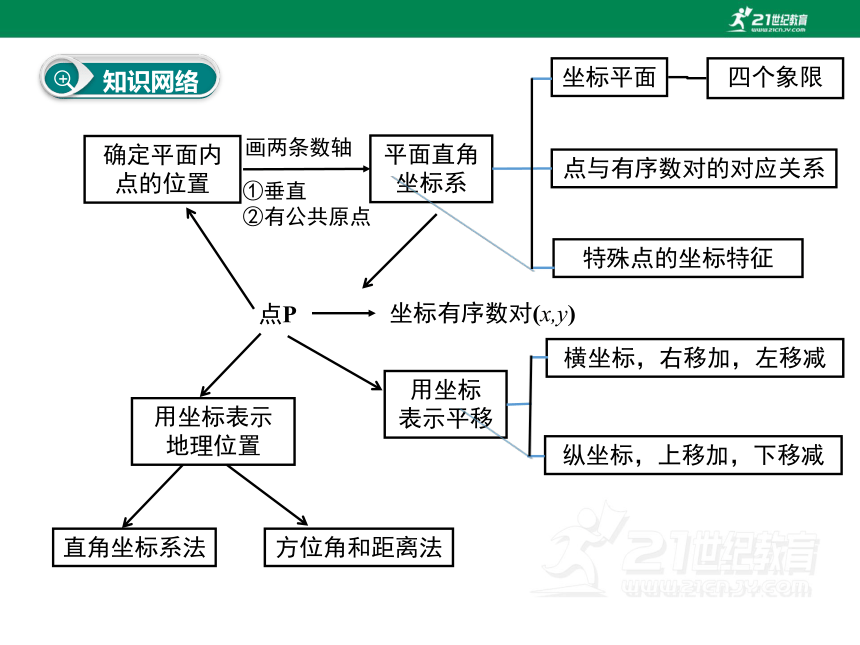
知识网络
确定平面内点的位置
平面直角
坐标系
坐标平面
四个象限
点与有序数对的对应关系
特殊点的坐标特征
点P
画两条数轴
①垂直
②有公共原点
坐标有序数对(x,y)
用坐标
表示平移
横坐标,右移加,左移减
纵坐标,上移加,下移减
用坐标表示
地理位置
直角坐标系法
方位角和距离法
专题复习
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则点a的值是 .
-2
专题一 平面直角坐标系与点的坐标
【归纳拓展】
1.第一、三象限内点的横、纵坐标同号;
2.第二、四象限内点的横、纵坐标异号;
3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的
距离是它横坐标的绝对值;
4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线
上的点的横坐标相同.
【迁移应用1】
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则
m的值为 .
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则
点B的坐标是 .
(2,2)或(-2,2)
【例2】如图,把三角形ABC经过一定的变换得到三角形A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 .
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
专题二 坐标与平移
【归纳拓展】为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行了怎样的平移.
【迁移应用2】
将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
-10
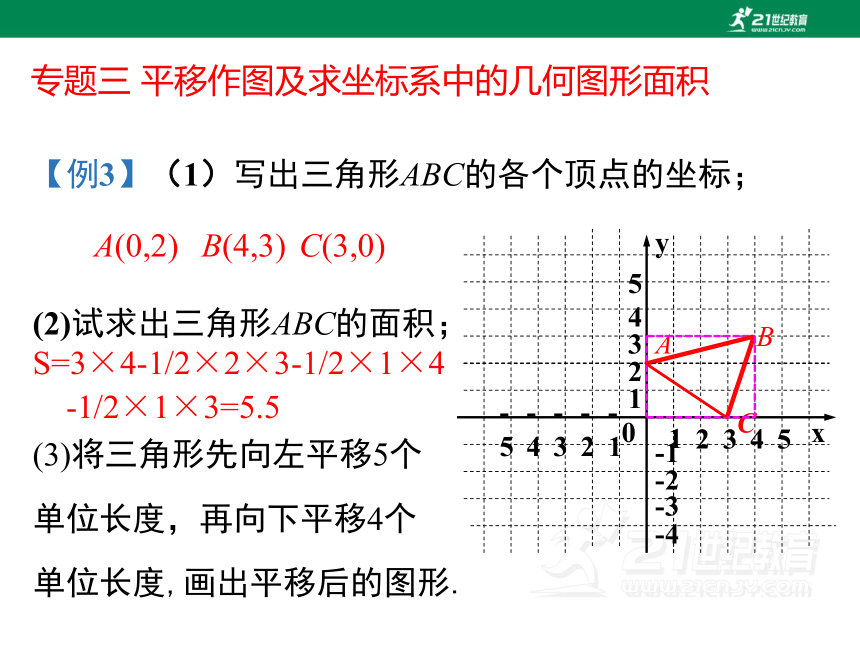
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A(0,2)
B(4,3)
C(3,0)
S=3×4-1/2×2×3-1/2×1×4
-1/2×1×3=5.5
专题三 平移作图及求坐标系中的几何图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转化为一些特殊的图形,去间接计算面积.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
【迁移应用3】
已知直角三角形ABC的直角边BC=AC,
且B(3,2),C(3,-2),求点A的坐标及三
角形ABC的面积.
A
B
C
O
x
y
解:∵B(3,2),C(3,-2),
∴BC∥y轴,且BC=2-(-2)=4,
∴AC=BC=4.
∴三角形ABC面积是1/2×4×4=8.
∵AC⊥BC,∴AC⊥y轴,
∴点A的横坐标为3-4=-1,纵坐标为-2,
∴A点坐标为(-1,-2).
课堂小结
平面直角坐标系
概念及
有关知识
坐标方法
的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移
课后训练
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的
坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标
是 .
(3 ,-2)
(-4 ,0)
3.点A(2,3)到x轴的距离为 ;点B(-4,0)到y
轴的距离为 ;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3 ,-1)
4.直角坐标系中,在y轴上有一点P ,且OP=5,则
P的坐标为 .
(0 ,5)或(0 ,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第7章小结与复习
人教版七年级下册
知识网络
确定平面内点的位置
平面直角
坐标系
坐标平面
四个象限
点与有序数对的对应关系
特殊点的坐标特征
点P
画两条数轴
①垂直
②有公共原点
坐标有序数对(x,y)
用坐标
表示平移
横坐标,右移加,左移减
纵坐标,上移加,下移减
用坐标表示
地理位置
直角坐标系法
方位角和距离法
专题复习
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的
距离为5,则点a的值是 .
-2
专题一 平面直角坐标系与点的坐标
【归纳拓展】
1.第一、三象限内点的横、纵坐标同号;
2.第二、四象限内点的横、纵坐标异号;
3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的
距离是它横坐标的绝对值;
4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线
上的点的横坐标相同.
【迁移应用1】
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则
m的值为 .
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则
点B的坐标是 .
(2,2)或(-2,2)
【例2】如图,把三角形ABC经过一定的变换得到三角形A′B′C′,如果三角形ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 .
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
专题二 坐标与平移
【归纳拓展】为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行了怎样的平移.
【迁移应用2】
将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
-10
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A(0,2)
B(4,3)
C(3,0)
S=3×4-1/2×2×3-1/2×1×4
-1/2×1×3=5.5
专题三 平移作图及求坐标系中的几何图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转化为一些特殊的图形,去间接计算面积.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积的需要.
【迁移应用3】
已知直角三角形ABC的直角边BC=AC,
且B(3,2),C(3,-2),求点A的坐标及三
角形ABC的面积.
A
B
C
O
x
y
解:∵B(3,2),C(3,-2),
∴BC∥y轴,且BC=2-(-2)=4,
∴AC=BC=4.
∴三角形ABC面积是1/2×4×4=8.
∵AC⊥BC,∴AC⊥y轴,
∴点A的横坐标为3-4=-1,纵坐标为-2,
∴A点坐标为(-1,-2).
课堂小结
平面直角坐标系
概念及
有关知识
坐标方法
的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移
课后训练
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的
坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标
是 .
(3 ,-2)
(-4 ,0)
3.点A(2,3)到x轴的距离为 ;点B(-4,0)到y
轴的距离为 ;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3 ,-1)
4.直角坐标系中,在y轴上有一点P ,且OP=5,则
P的坐标为 .
(0 ,5)或(0 ,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
