平面图形的认识整理与练习(课件)-六年级下册数学苏教版(共20张PPT)
文档属性
| 名称 | 平面图形的认识整理与练习(课件)-六年级下册数学苏教版(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-04 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
平面图形的认识整理与复习(1)
A
B
C
有3条线段,是线段 AB、线段 AC、线段 BC。
有6条射线,分别是每个点分成的两条。
只有一条直线,是直线 AB。
答:
如果直线上有4个点,则有射线( )条,线段( )条;
如果直线上有5个点,则有射线( )条,线段( )条;
如果直线上有n个点,则有射线( )条,线段( )条。
8
6
10
10
2n
下图中,有几条线段,几条射线,几条直线?
8
6
10
10
2n
数学小讲师
射线
直线
线段
角
三角形
平面图形的认识中我们学习了哪些重要的概念?
正方形
长方形
平行四边形
梯形
量角器
量角
画角
圆
两点间的距离
互相平行
互相垂直
锐角
周角
平角
钝角
直角
相交
提出问题
射线
直线
线段
角
两点间的距离
量角器
互相平行
相交
互相垂直
锐角
周角
平角
钝角
直角
量角
画角
a
b
a
b
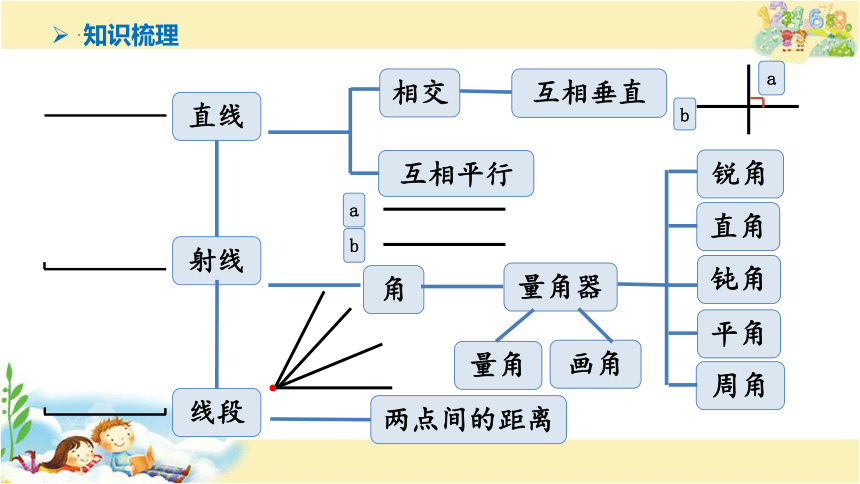
知识梳理
1.直线、射线和线段各有什么特征?它们之间有什么关系?
2.怎样的两条直线互相垂直?怎样的两条直线互相平行?
3.角的大小与什么有关?计量角的大小的单位是什么?怎样用量角器、画角?
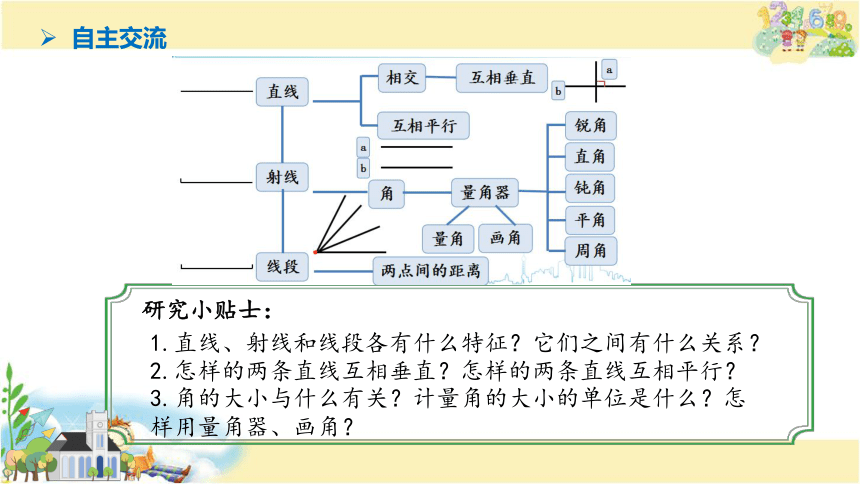
研究小贴士:
自主交流
直线、射线和线段各有什么特征?它们之间有什么关系?
线段
射线
直线
有两个端点
可以测量
有一个端点
不可测量
没有端点
不可测量
都是直的
线段
射线
直线
不同点
相同点
名称
图形
汇报交流
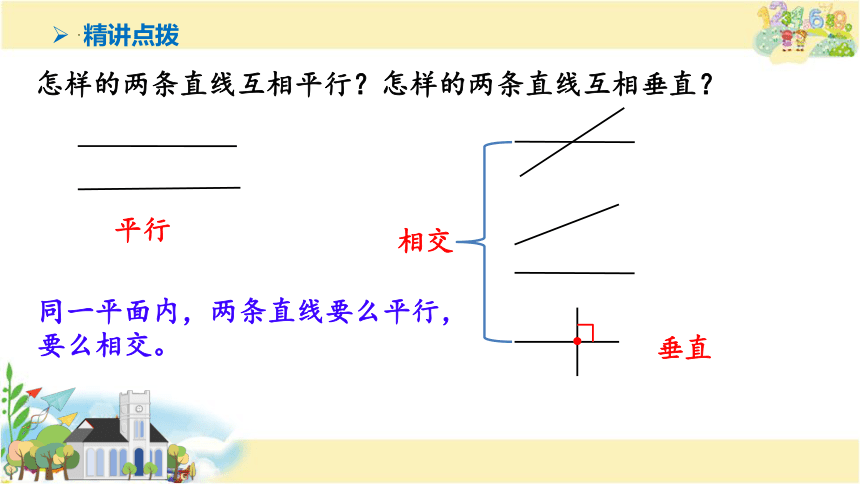
怎样的两条直线互相平行?怎样的两条直线互相垂直?
同一平面内,两条直线要么平行,要么相交。
平行
垂直
相交
精讲点拨
1. 要把一根木条固定在墙上,至少需要钉几枚钉子?为什么?
答:因为两点确定一条直线,所以至少需要两枚钉子把一根木条固定在墙上。
练习实践
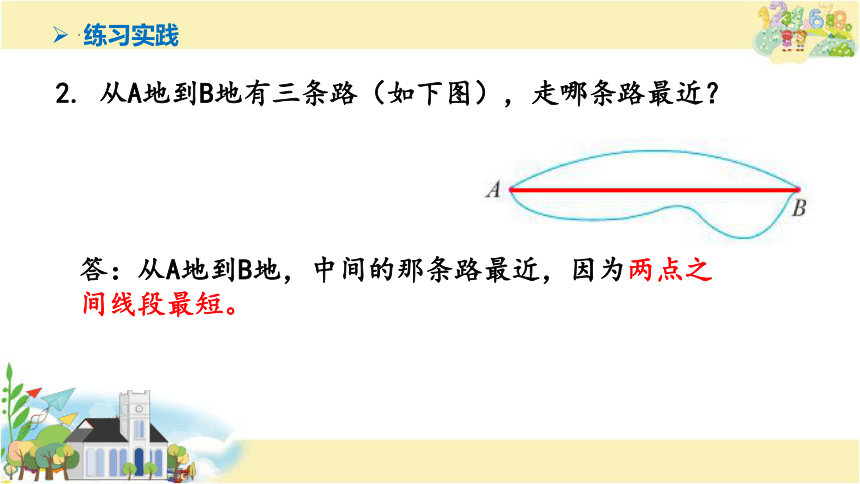
2. 从A地到B地有三条路(如下图),走哪条路最近?
答:从A地到B地,中间的那条路最近,因为两点之间线段最短。
练习实践
3. 在天然气主管道两侧的A、B两个小区各接一条管道与主管道连通,怎么接用材料最节省?在图中画出来。
A
B
答:如图最节省,因为点到直线间的距离垂直线段最短。
主管道
练习实践
从一个顶点引出的两条射线,就组成一个角.
角
汇报交流
顶点
边
边
角的大小与什么有关?
角的大小与两边的长短没有关系。
角的大小与两条边叉开的大小有关。
汇报与交流
中心
外圈刻度线
内圈刻度线
精讲点拨
把半圆分成180等份,每一份所对的角是1度角。“度”是角的计量单位,用符号“°”表示,如1度记作1°。
1
∠1=30°
量角的步骤:
怎样用量角器量出∠1的度数?
量角
中心和角的顶点重合
零刻度线和角的一条边重合
看角的另一边指的刻度
精讲点拨
画角
一画线
二重合
三找点
四连线
画一个的角。
精讲点拨
五标角
角的分类
知识梳理
锐角<直角<钝角<平角<周角
1个周角=2个平角=4个平角
锐角、直角、钝角、平角、周角
名 称
图 形
特 征
锐 角
直 角
钝 角
平 角
周 角
小于90°
等于90°
大于90°
小于180°
等于180°
等于360°
4.画一画,填一填。
练习实践
5. 先估计下面每个角的度数,再用量角器量一量。
测量
测量
测量
50
145
90
练习实践
拓展应用
如图,在四边形内找一个点O,使它到四边形四个顶点的距离之和最小,并说明理由。
理由:两点之间线段最短。
0
回顾与反思
这节课我们复习了哪些内容?你有什么新的收获和体会?
平面图形的认识整理与复习(1)
A
B
C
有3条线段,是线段 AB、线段 AC、线段 BC。
有6条射线,分别是每个点分成的两条。
只有一条直线,是直线 AB。
答:
如果直线上有4个点,则有射线( )条,线段( )条;
如果直线上有5个点,则有射线( )条,线段( )条;
如果直线上有n个点,则有射线( )条,线段( )条。
8
6
10
10
2n
下图中,有几条线段,几条射线,几条直线?
8
6
10
10
2n
数学小讲师
射线
直线
线段
角
三角形
平面图形的认识中我们学习了哪些重要的概念?
正方形
长方形
平行四边形
梯形
量角器
量角
画角
圆
两点间的距离
互相平行
互相垂直
锐角
周角
平角
钝角
直角
相交
提出问题
射线
直线
线段
角
两点间的距离
量角器
互相平行
相交
互相垂直
锐角
周角
平角
钝角
直角
量角
画角
a
b
a
b
知识梳理
1.直线、射线和线段各有什么特征?它们之间有什么关系?
2.怎样的两条直线互相垂直?怎样的两条直线互相平行?
3.角的大小与什么有关?计量角的大小的单位是什么?怎样用量角器、画角?
研究小贴士:
自主交流
直线、射线和线段各有什么特征?它们之间有什么关系?
线段
射线
直线
有两个端点
可以测量
有一个端点
不可测量
没有端点
不可测量
都是直的
线段
射线
直线
不同点
相同点
名称
图形
汇报交流
怎样的两条直线互相平行?怎样的两条直线互相垂直?
同一平面内,两条直线要么平行,要么相交。
平行
垂直
相交
精讲点拨
1. 要把一根木条固定在墙上,至少需要钉几枚钉子?为什么?
答:因为两点确定一条直线,所以至少需要两枚钉子把一根木条固定在墙上。
练习实践
2. 从A地到B地有三条路(如下图),走哪条路最近?
答:从A地到B地,中间的那条路最近,因为两点之间线段最短。
练习实践
3. 在天然气主管道两侧的A、B两个小区各接一条管道与主管道连通,怎么接用材料最节省?在图中画出来。
A
B
答:如图最节省,因为点到直线间的距离垂直线段最短。
主管道
练习实践
从一个顶点引出的两条射线,就组成一个角.
角
汇报交流
顶点
边
边
角的大小与什么有关?
角的大小与两边的长短没有关系。
角的大小与两条边叉开的大小有关。
汇报与交流
中心
外圈刻度线
内圈刻度线
精讲点拨
把半圆分成180等份,每一份所对的角是1度角。“度”是角的计量单位,用符号“°”表示,如1度记作1°。
1
∠1=30°
量角的步骤:
怎样用量角器量出∠1的度数?
量角
中心和角的顶点重合
零刻度线和角的一条边重合
看角的另一边指的刻度
精讲点拨
画角
一画线
二重合
三找点
四连线
画一个的角。
精讲点拨
五标角
角的分类
知识梳理
锐角<直角<钝角<平角<周角
1个周角=2个平角=4个平角
锐角、直角、钝角、平角、周角
名 称
图 形
特 征
锐 角
直 角
钝 角
平 角
周 角
小于90°
等于90°
大于90°
小于180°
等于180°
等于360°
4.画一画,填一填。
练习实践
5. 先估计下面每个角的度数,再用量角器量一量。
测量
测量
测量
50
145
90
练习实践
拓展应用
如图,在四边形内找一个点O,使它到四边形四个顶点的距离之和最小,并说明理由。
理由:两点之间线段最短。
0
回顾与反思
这节课我们复习了哪些内容?你有什么新的收获和体会?
