物理人教版(2019)必修第二册5.2 运动的合成与分解(共15张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册5.2 运动的合成与分解(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 32.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-02-05 09:17:28 | ||
图片预览





文档简介
(共15张PPT)
运动的合成与分解
对于直线运动中,建立一维坐标,据运动规律,就可以确定任意时刻的位置,进而知道它的运动轨迹。如果研究复杂的运动,我们怎么办呢?
汽车延直线公路行驶
翻滚的过山车
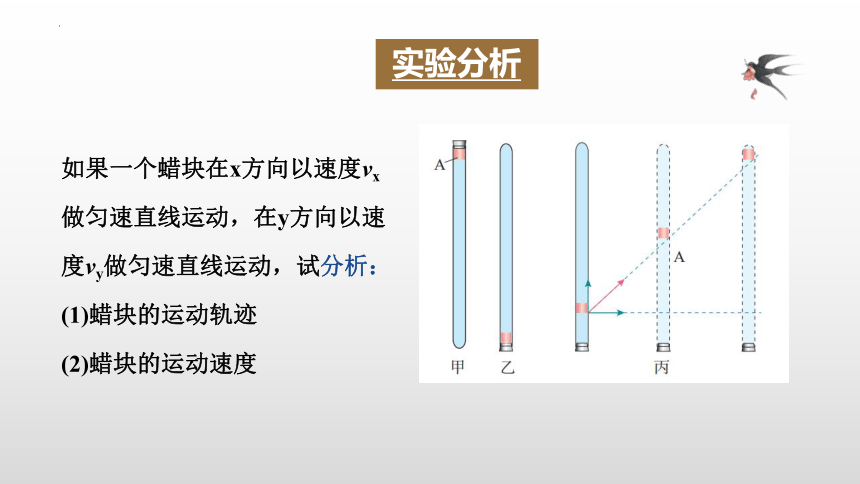
如果一个蜡块在x方向以速度vx做匀速直线运动,在y方向以速度vy做匀速直线运动,试分析:
(1)蜡块的运动轨迹
(2)蜡块的运动速度
实验分析
1.将放有红蜡块的玻璃管倒置在水平的电动滑轨上,向右匀速运动,则红蜡块的运动轨迹是怎样的呢?
观察红蜡块的运动
水平向右的匀速直线运动
2 .将玻璃管中注满清水并倒放静置,则红蜡块的运动轨迹是怎样的呢?
竖直向上的匀速直线运动
观察红蜡块的运动
3 .将玻璃管中注满清水,并倒置在电动滑轨上,则红蜡块的运动轨迹是怎样的呢?
斜向右上方的直线运动
斜向右上方的运动是否是匀速的呢?
定量研究:
因为红蜡块既在向上匀速运动,又在向右匀速运动,所以它在黑色背景平面内运动,故可以建立平面直角坐标系来描述它在任意时刻的运动情况。
观察红蜡块的运动
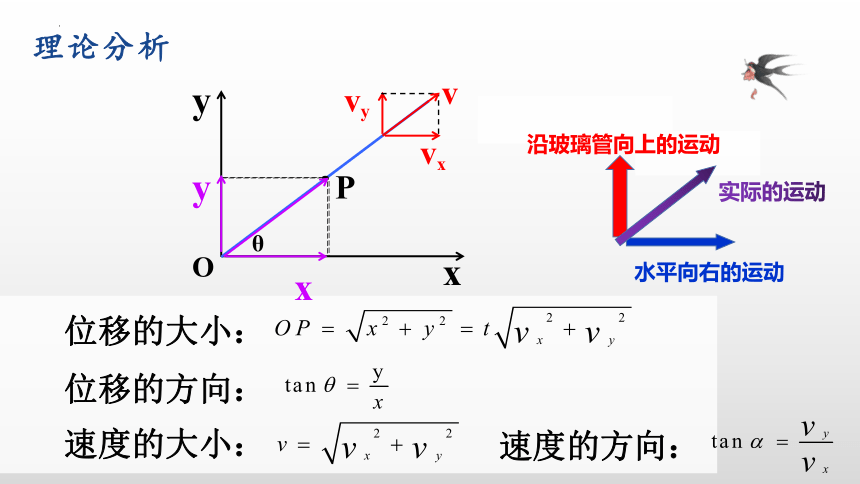
理论分析
O
x
y
P
θ
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
速度的方向:
水平向右的运动
沿玻璃管向上的运动
实际的运动
总结与归纳
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3、由分运动求合运动的过程叫运动的合成
4、由合运动求分运动的过程叫运动的分解
合运动与分运动的关系
运动的独立性
运动的等时性
运动的等效性
运动的同体性
运动的合成与分解
合运动
分运动
运动的合成
运动的分解
⑴分解原则:根据运动的实际效果分解,也可以正交分解。
⑵遵循规律:平行四边形法则
a
a1
a2
v1
v2
v
⑶运动的合成与分解是指 x、v、 a 的合成与分解。
A
B
x
x1
x2
位移的合成
速度的合成
加速度的合成
运动的合成是唯一的,而分解不是唯一的,通常按运动所产生的实际效果分解
(1)两个都是从静止开始的互成角度匀加速直线运动的合运动是什么运动?
(2)两个初速度都不为零互成角度匀加速直线运动的合运动是什么运动?
一定是匀加速直线运动
可能是匀变速直线运动,也有可能是匀变速曲线运动
v
v2
v1
a1
a2
a
v
v2
v1
a1
a2
a
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
如图所示,在一张白纸上放置一根直尺,沿直尺的边缘放置一块直角三角板.将三角板沿直尺水平向右匀速直线运动,同时将一支铅笔从三角板直角边的最下端沿直角边向上运动,而且向上的速度越来越大,则铅笔在纸上留下的痕迹可能是( )
A. B. C. D.
C
【例题】如图所示,红蜡块能在竖直放置并装满水的玻璃管中匀速上升,若红蜡块从A点开始,沿玻璃管匀速上升的同时,使玻璃管水平向右做直线运动且玻璃管到CD处时红蜡块恰在D点,则下列说法不正确的是 ( )
A.若玻璃管匀速运动,则蜡块的轨迹为直线P
B.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线R
C.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线Q
D.若玻璃管匀减速运动,则蜡块的轨迹可能为曲线R
B
【例题】在光滑的水平面上建立xOy平面直角坐标系,一质点在水平面上从坐标原点开始运动,沿x方向和y方向的xt图像和vyt图像分别如图甲、乙所示,则0~4 s内 ( )
A.质点的运动轨迹为直线
B.质点的加速度大小恒为2 m/s2
C.4 s末质点的速度大小为2 m/s
D.4 s末质点离坐标原点的距离为16 m
C
结
束
运动的合成与分解
对于直线运动中,建立一维坐标,据运动规律,就可以确定任意时刻的位置,进而知道它的运动轨迹。如果研究复杂的运动,我们怎么办呢?
汽车延直线公路行驶
翻滚的过山车
如果一个蜡块在x方向以速度vx做匀速直线运动,在y方向以速度vy做匀速直线运动,试分析:
(1)蜡块的运动轨迹
(2)蜡块的运动速度
实验分析
1.将放有红蜡块的玻璃管倒置在水平的电动滑轨上,向右匀速运动,则红蜡块的运动轨迹是怎样的呢?
观察红蜡块的运动
水平向右的匀速直线运动
2 .将玻璃管中注满清水并倒放静置,则红蜡块的运动轨迹是怎样的呢?
竖直向上的匀速直线运动
观察红蜡块的运动
3 .将玻璃管中注满清水,并倒置在电动滑轨上,则红蜡块的运动轨迹是怎样的呢?
斜向右上方的直线运动
斜向右上方的运动是否是匀速的呢?
定量研究:
因为红蜡块既在向上匀速运动,又在向右匀速运动,所以它在黑色背景平面内运动,故可以建立平面直角坐标系来描述它在任意时刻的运动情况。
观察红蜡块的运动
理论分析
O
x
y
P
θ
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
速度的方向:
水平向右的运动
沿玻璃管向上的运动
实际的运动
总结与归纳
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3、由分运动求合运动的过程叫运动的合成
4、由合运动求分运动的过程叫运动的分解
合运动与分运动的关系
运动的独立性
运动的等时性
运动的等效性
运动的同体性
运动的合成与分解
合运动
分运动
运动的合成
运动的分解
⑴分解原则:根据运动的实际效果分解,也可以正交分解。
⑵遵循规律:平行四边形法则
a
a1
a2
v1
v2
v
⑶运动的合成与分解是指 x、v、 a 的合成与分解。
A
B
x
x1
x2
位移的合成
速度的合成
加速度的合成
运动的合成是唯一的,而分解不是唯一的,通常按运动所产生的实际效果分解
(1)两个都是从静止开始的互成角度匀加速直线运动的合运动是什么运动?
(2)两个初速度都不为零互成角度匀加速直线运动的合运动是什么运动?
一定是匀加速直线运动
可能是匀变速直线运动,也有可能是匀变速曲线运动
v
v2
v1
a1
a2
a
v
v2
v1
a1
a2
a
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
如图所示,在一张白纸上放置一根直尺,沿直尺的边缘放置一块直角三角板.将三角板沿直尺水平向右匀速直线运动,同时将一支铅笔从三角板直角边的最下端沿直角边向上运动,而且向上的速度越来越大,则铅笔在纸上留下的痕迹可能是( )
A. B. C. D.
C
【例题】如图所示,红蜡块能在竖直放置并装满水的玻璃管中匀速上升,若红蜡块从A点开始,沿玻璃管匀速上升的同时,使玻璃管水平向右做直线运动且玻璃管到CD处时红蜡块恰在D点,则下列说法不正确的是 ( )
A.若玻璃管匀速运动,则蜡块的轨迹为直线P
B.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线R
C.若玻璃管匀加速运动,则蜡块的轨迹可能为曲线Q
D.若玻璃管匀减速运动,则蜡块的轨迹可能为曲线R
B
【例题】在光滑的水平面上建立xOy平面直角坐标系,一质点在水平面上从坐标原点开始运动,沿x方向和y方向的xt图像和vyt图像分别如图甲、乙所示,则0~4 s内 ( )
A.质点的运动轨迹为直线
B.质点的加速度大小恒为2 m/s2
C.4 s末质点的速度大小为2 m/s
D.4 s末质点离坐标原点的距离为16 m
C
结
束
