17.1.1勾股定理 课件(共34张PPT)
文档属性
| 名称 | 17.1.1勾股定理 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 09:46:26 | ||
图片预览







文档简介
(共34张PPT)
17.1.1勾股定理
人教版八年级下册
知识回顾
一般三角形
1.三角形内角和为180 .
2.两边之和大于第三边,
两边之差小于第三边.
直角三角形
1.两锐角互余.
2.两边之和大于第三边,
两边之差小于第三边.
3.斜边中线等于斜边一半.
4.三角形内角和为180 .
教学目标
1.探索并掌握勾股定理的证明过程.
2.熟练运用勾股定理解决数学问题.
新知导入
毕达哥拉斯是古希腊著名的数学家,相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的三边的某种数量关系.
请你观察一下地面的图案,从中发现了什么?
新知讲解
知识点:勾股定理的认识与证明
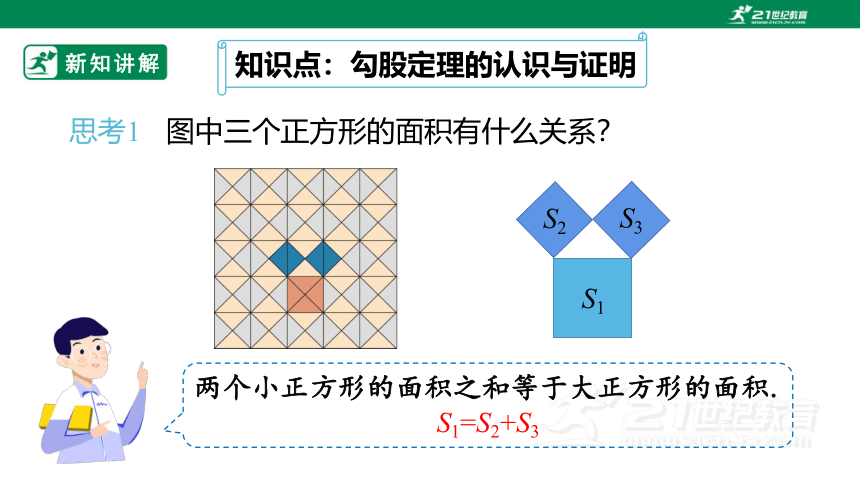
思考1 图中三个正方形的面积有什么关系?
两个小正方形的面积之和等于大正方形的面积.
S1=S2+S3
新知讲解
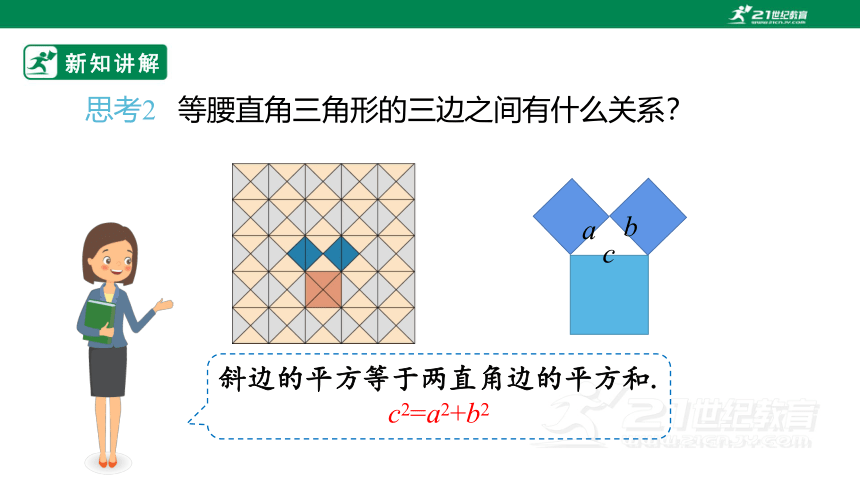
思考2 等腰直角三角形的三边之间有什么关系?
a
b
c
斜边的平方等于两直角边的平方和.
c2=a2+b2
新知讲解
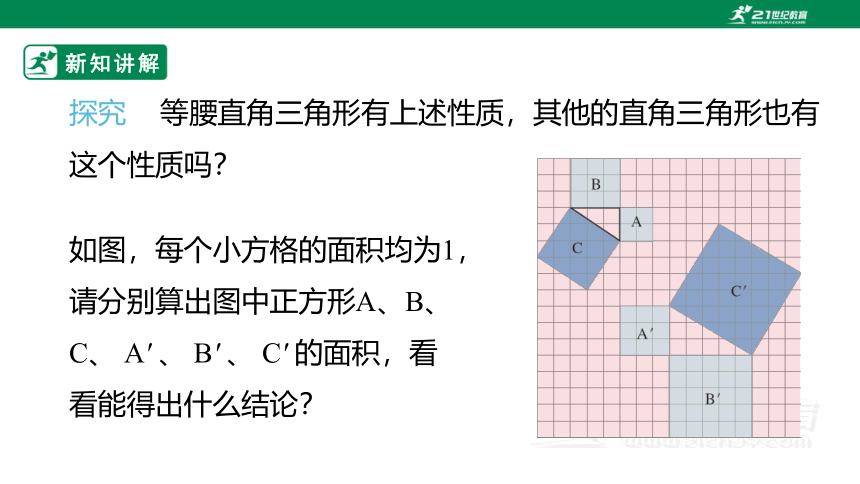
探究 等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
如图,每个小方格的面积均为1,请分别算出图中正方形A、B、C、 A' 、 B' 、 C' 的面积,看看能得出什么结论?
新知讲解
A B C A’ B’ C’
面积/格
4
34
25
9
13
9
你发现了什么规律吗?
我发现 SA+SB=SC、SA'+SB'=SC'
新知讲解
命题1:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么.
通过上面的思考和探究,我们可以猜想:
有哪些证明方法呢?
是不是所有的直角三角形都具有这样的结论呢?
这就需要我们对一般的直角三角形进行证明.
新知讲解
a
b
b
c
a
b
c
a
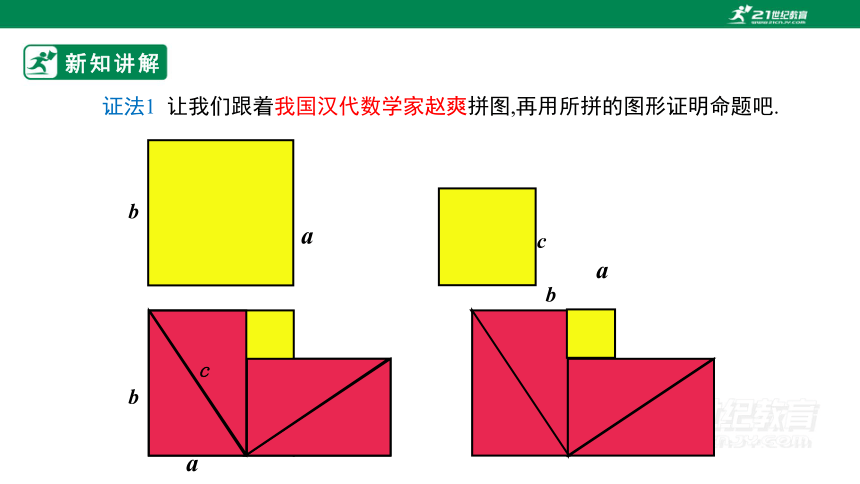
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
新知讲解
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
新知讲解
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
新知讲解
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
新知讲解
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
证明:
证法3 刘徽“青朱出入图”
a
b
c
青出
青出
青入
青入
朱入
朱出
设大正方形的面积为S,则S=
根据“出入相补,以盈补虚”的原理,得S=.
所以,得=.
青方
朱方
新知讲解
a、b、c为正数
如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
公式变形
勾股定理
a
b
c
新知讲解
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
数学小知识
新知讲解
1.勾股定理是直角三角形的特殊性质,所以其适用的前提是直角三角形.
2.运用勾股定理时,一定要分清直角边和斜边,若没有明确哪条边是斜边,则需要分类讨论,写出所有可能的情况,以避免漏解或者错解.
新知典例
如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理,得
(2)据勾股定理,得
C
A
B
例1
新知练习
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a、c.
【1】在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x.根据勾股定理建立方程,得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程,得
(2x)2-x2=152,
解得
归纳:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
新知练习
【2】 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
归纳:当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
新知典例
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式可知,
AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
归纳:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
例2
新知练习
解:
教师点拨:
作高巧构直角三角形,再利用勾股定理和30°的角求解.
过点A作AD⊥BC,
∵∠BAD=30°,
【3】如图,已知在△ABC中,∠B=60°,AC=70,AB=30,求BC的长.
根据勾股定理,在Rt△ABD中, AD2=AB2-BD2=302-152=675,
根据勾股定理,在Rt△ACD中,CD=
∴BC=BD+DC=15+65=80.
D
新知典例
求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144 =x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5.
例3
新知练习
【4】如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形 A、B、C、D 的边长分别为12、16、9、12,求最大正方形 E 的面积.
新知练习
解:设另两个正方形中大的为M,小的为N,
由勾股定理和正方形的面积公式,得
,
而
课堂总结
勾股定理
证明
定理
赵爽弦图
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
新知练习
A
B
课堂练习
5
12
课堂练习
5.某直角三角形一直角边长为3,另一直角边和斜边的和为9,求斜边的长为多少?
解:设斜边长为 x,则另一直角边长为 9- x.
由勾股定理得:
化简得:
答:斜边长为5.
解得: , .
课堂练习
6.如图,在△中,AB=13,BC=14,AC=15,求边BC上的高AD的长.
解:设BD=x(x>0),则CD=14-x.
在Rt△ABC中,由勾股定理得,
同理,在Rt△ABD中,
所以,解得x=5.
所以=144,即AD=12.
课堂练习
解:∵AE=BE,
∴S△ABE= AE·BE= AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE= AB2= .
同理可得,S△AHC+S△BCF= AC2+ BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为 AB2= .
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直
角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.1.1勾股定理
人教版八年级下册
知识回顾
一般三角形
1.三角形内角和为180 .
2.两边之和大于第三边,
两边之差小于第三边.
直角三角形
1.两锐角互余.
2.两边之和大于第三边,
两边之差小于第三边.
3.斜边中线等于斜边一半.
4.三角形内角和为180 .
教学目标
1.探索并掌握勾股定理的证明过程.
2.熟练运用勾股定理解决数学问题.
新知导入
毕达哥拉斯是古希腊著名的数学家,相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的三边的某种数量关系.
请你观察一下地面的图案,从中发现了什么?
新知讲解
知识点:勾股定理的认识与证明
思考1 图中三个正方形的面积有什么关系?
两个小正方形的面积之和等于大正方形的面积.
S1=S2+S3
新知讲解
思考2 等腰直角三角形的三边之间有什么关系?
a
b
c
斜边的平方等于两直角边的平方和.
c2=a2+b2
新知讲解
探究 等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
如图,每个小方格的面积均为1,请分别算出图中正方形A、B、C、 A' 、 B' 、 C' 的面积,看看能得出什么结论?
新知讲解
A B C A’ B’ C’
面积/格
4
34
25
9
13
9
你发现了什么规律吗?
我发现 SA+SB=SC、SA'+SB'=SC'
新知讲解
命题1:如果直角三角形的两条直角边长分别为a、b,斜边长为c,那么.
通过上面的思考和探究,我们可以猜想:
有哪些证明方法呢?
是不是所有的直角三角形都具有这样的结论呢?
这就需要我们对一般的直角三角形进行证明.
新知讲解
a
b
b
c
a
b
c
a
证法1 让我们跟着我国汉代数学家赵爽拼图,再用所拼的图形证明命题吧.
新知讲解
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因为,这个图案被选为2002年在北京召开的国际数学大会的会徽.
新知讲解
证法2 毕达哥拉斯证法,请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
新知讲解
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:
∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
新知讲解
a
a
b
b
c
c
∴a2 + b2 = c2.
证法3 美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
证明:
证法3 刘徽“青朱出入图”
a
b
c
青出
青出
青入
青入
朱入
朱出
设大正方形的面积为S,则S=
根据“出入相补,以盈补虚”的原理,得S=.
所以,得=.
青方
朱方
新知讲解
a、b、c为正数
如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
公式变形
勾股定理
a
b
c
新知讲解
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
数学小知识
新知讲解
1.勾股定理是直角三角形的特殊性质,所以其适用的前提是直角三角形.
2.运用勾股定理时,一定要分清直角边和斜边,若没有明确哪条边是斜边,则需要分类讨论,写出所有可能的情况,以避免漏解或者错解.
新知典例
如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理,得
(2)据勾股定理,得
C
A
B
例1
新知练习
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a、c.
【1】在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x.根据勾股定理建立方程,得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程,得
(2x)2-x2=152,
解得
归纳:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
新知练习
【2】 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
归纳:当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
新知典例
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式可知,
AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
归纳:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
例2
新知练习
解:
教师点拨:
作高巧构直角三角形,再利用勾股定理和30°的角求解.
过点A作AD⊥BC,
∵∠BAD=30°,
【3】如图,已知在△ABC中,∠B=60°,AC=70,AB=30,求BC的长.
根据勾股定理,在Rt△ABD中, AD2=AB2-BD2=302-152=675,
根据勾股定理,在Rt△ACD中,CD=
∴BC=BD+DC=15+65=80.
D
新知典例
求下列图中未知数x、y的值:
解:由勾股定理可得
81+ 144 =x2,
解得x=15.
解:由勾股定理可得
y2+ 144=169,
解得 y=5.
例3
新知练习
【4】如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形 A、B、C、D 的边长分别为12、16、9、12,求最大正方形 E 的面积.
新知练习
解:设另两个正方形中大的为M,小的为N,
由勾股定理和正方形的面积公式,得
,
而
课堂总结
勾股定理
证明
定理
赵爽弦图
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
新知练习
A
B
课堂练习
5
12
课堂练习
5.某直角三角形一直角边长为3,另一直角边和斜边的和为9,求斜边的长为多少?
解:设斜边长为 x,则另一直角边长为 9- x.
由勾股定理得:
化简得:
答:斜边长为5.
解得: , .
课堂练习
6.如图,在△中,AB=13,BC=14,AC=15,求边BC上的高AD的长.
解:设BD=x(x>0),则CD=14-x.
在Rt△ABC中,由勾股定理得,
同理,在Rt△ABD中,
所以,解得x=5.
所以=144,即AD=12.
课堂练习
解:∵AE=BE,
∴S△ABE= AE·BE= AE2.
又∵AE2+BE2=AB2,
∴2AE2=AB2,
∴S△ABE= AB2= .
同理可得,S△AHC+S△BCF= AC2+ BC2.
又∵AC2+BC2=AB2,
∴阴影部分的面积为 AB2= .
7.如图,以Rt△ABC的三边长为斜边分别向外作等腰直
角三角形.若斜边AB=3,求△ABE及阴影部分的面积.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
