人教版八年级下册19.2一次函数 练习(含答案)
文档属性
| 名称 | 人教版八年级下册19.2一次函数 练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 953.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 15:01:20 | ||
图片预览

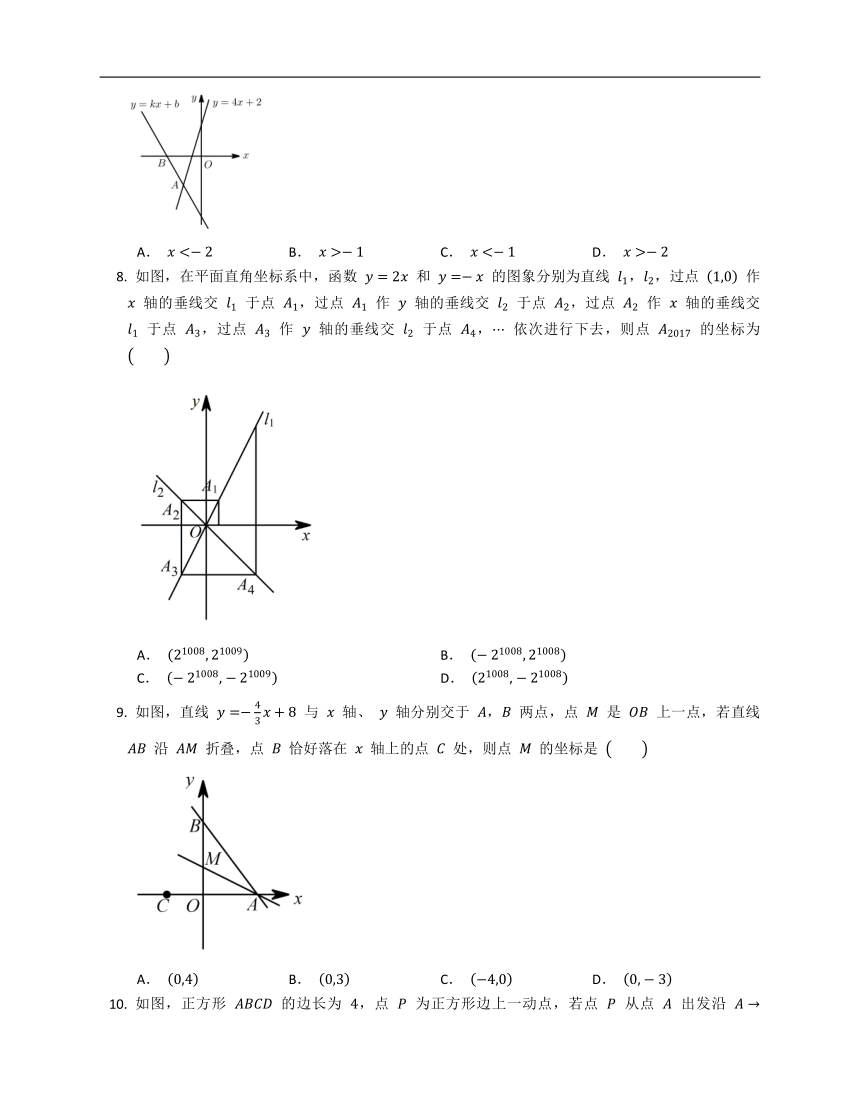
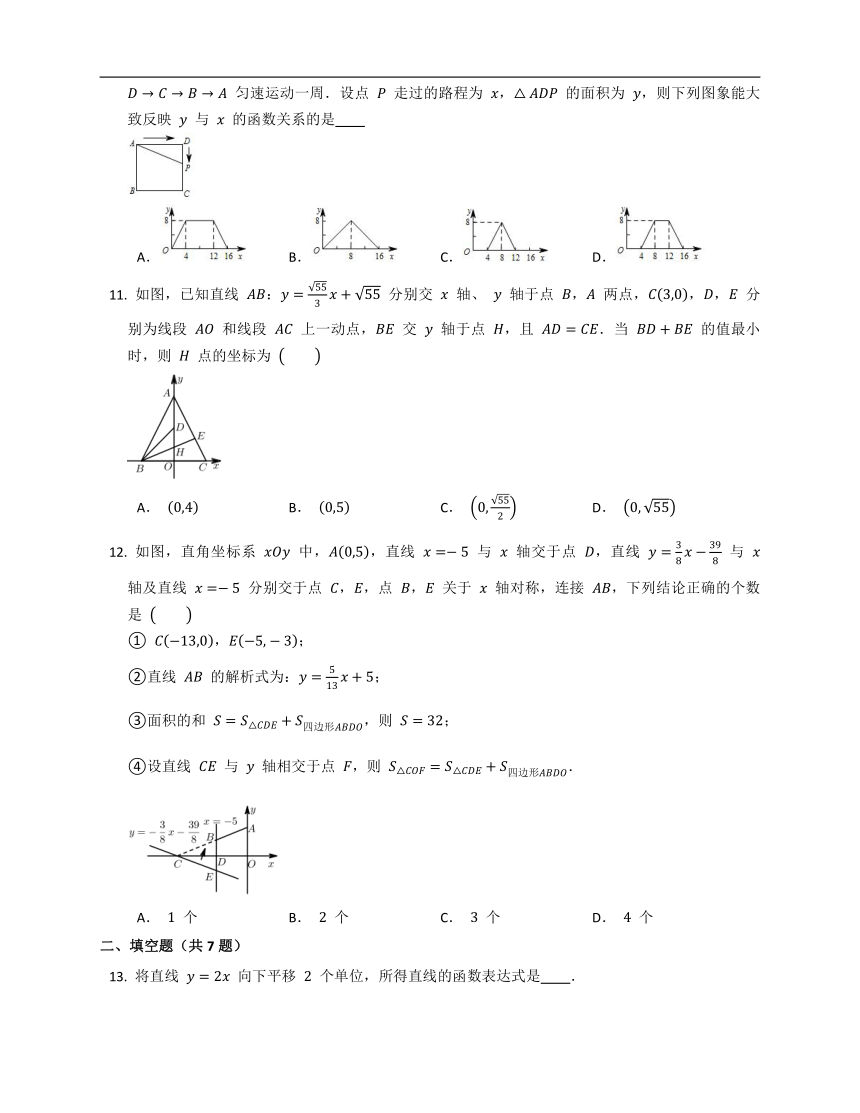


文档简介
19.2一次函数
一、选择题(共12题)
下列说法正确的是
A.过原点的直线都是正比例函数 B.正比例函数图象经过原点
C. 是正比例函数 D. 是正比例函数
下列函数中,是一次函数的有
();();();();().
A. 个 B. 个 C. 个 D. 个
当 时,一次函数 的图象不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
对于函数 ,下列结论正确的是
A.它的图象必经过点 B.它的图象经过第一、二、四象限
C.当 时, D. 的值随 值的增大而增大
一次函数 的图象大致是
A. B. C. D.
如图,直线 与 轴、 轴分别交于点 和点 ,点 , 分别为线段 , 的中点,点 为 上一动点,当 最小时,点 的坐标为
A. B. C. D.
(2018·金华市东阳市·期末)如图,经过点 的直线 与直线 相交于点 ,则不等式 的解集为
A. B. C. D.
如图,在平面直角坐标系中,函数 和 的图象分别为直线 ,,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 , 依次进行下去,则点 的坐标为
A. B.
C. D.
如图,直线 与 轴、 轴分别交于 , 两点,点 是 上一点,若直线 沿 折叠,点 恰好落在 轴上的点 处,则点 的坐标是
A. B. C. D.
如图,正方形 的边长为 ,点 为正方形边上一动点,若点 从点 出发沿 匀速运动一周.设点 走过的路程为 , 的面积为 ,则下列图象能大致反映 与 的函数关系的是
A. B. C. D.
如图,已知直线 : 分别交 轴、 轴于点 , 两点,,, 分别为线段 和线段 上一动点, 交 轴于点 ,且 .当 的值最小时,则 点的坐标为
A. B. C. D.
如图,直角坐标系 中,,直线 与 轴交于点 ,直线 与 轴及直线 分别交于点 ,,点 , 关于 轴对称,连接 ,下列结论正确的个数是
① ,;
②直线 的解析式为:;
③面积的和 ,则 ;
④设直线 与 轴相交于点 ,则 .
A. 个 B. 个 C. 个 D. 个
二、填空题(共7题)
将直线 向下平移 个单位,所得直线的函数表达式是 .
在一次函数 中, 随 的增大而增大,则 的取值范围是 .
如图,利用函数图象可知方程组的解为 .
一次函数 的图象上有两点 和 ,且 ,则 与 的大小关系为 .
如图,在平面直角坐标系中,函数 与 的图象交于点 ,则不等式 的解集为 .
关于 的一元一次不等式组 有解,则直线 不经过第 象限.
如图,点 的坐标为 ,点 在直线 上运动,连接 ,则线段 的长的最小值为 .
三、解答题(共7题)
早晨 点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离 (千米)与他离校的时间 (小时)之间的图象.根据图象,完成下面问题:
(1) 小明乘车去保护区的速度是 千米/小时,线段 所表示的 与 的关系式是 ;
(2) 已知下午 点时,小明距保护区 千米,问他何时才能回到学校?
如图,直线 的解析表达式为 ,且 与 轴交于点 ,直线 经过点 ,,直线 和 交于点 .
(1) 求直线 的解析表达式.
(2) 求 的面积.
(3) 直线 上存在异于点 的另一点 ,使 与 面积相等,求出点 的坐标.
面对资源紧缺与环境保护问题,发展电动汽车成为汽车工业发展的主流趋势.我国某著名汽车制造厂开发了一款新式电动汽车,计划一年生产安装 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现: 名熟练工和 名新工人每月可安装 辆电动汽车; 名熟练工和 名新工人每月可安装 辆电动汽车.
(1) 每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2) 如果工厂招聘 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3) 在()的条件下,工厂给安装电动汽车的每名熟练工每月发 元的工资,给每名新工人每月发 元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额 (元)尽可能的少?
“绿水青山就是金山银山”.为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥.甲、乙两个仓库分别可运出 吨和 吨有机化肥;A,B两个果园分别需用 吨和 吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
设甲仓库运往A果园 吨有机化肥,若汽车每吨每千米的运费为 元.
(1) 根据题意,填写下表.
(2) 设总运费为 元,求 关于 的函数表达式,并求出当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
如图,直角坐标系 中,一次函数 的图象 分别与 , 轴交于 , 两点,正比例函数的图象 与 交于点 .
(1) 求 的值及 的解析式.
(2) 求 的值.
(3) 一次函数 的图象为 ,且 ,, 不能围成三角形,直接写出 的值.
在平面直角坐标系中,点 的坐标为 ,点 的变换点 的坐标定义如下:当 时,点 的坐标为 ,当 时,点 的坐标为 .
(1) ①求 的变换点坐标 .
②若点 的变换点为 ,连接 ,,则 .
③由上面二个问题的解决,请思考:
当点 的变换点为 时,点 与 是 变换.
当点 的变换点为 时,点 与 是 变换.(选填“轴对称”或“旋转”或“中心对称”或“平移”)
(2) 直线 上所有点的变换点组成一个新图形记为 ,请求出 的解析式.
(3) 如图①,直线 上所有点的变换点组成一个新图形记为 ,请在图①中画出图形 .
(4) 点 在直线 上,点 是点 的变换点,连接 ,直接写出 的取值范围.
如图,在坐标系中,四边形 的顶点 是坐标原点,点 在第一象限,点 在第四象限、点 在 轴的正半轴上. 且 ,, 的长分别是二元一次方程组 的解 .
(1) 求点 和点 的坐标.
(2) 点 是线段 上的动点(点 不与点 , 重合),过点 的直线 与 轴平行,直线 交边 或边 点 ,交边 或边 于点 .设点 的横坐标为 ,线段 的长度为 .已知 时,直线 恰好过点 .
①求 关于 的函数关系式.
②当 时,求点 的横坐标 的值.
答案
一、选择题(共12题)
1. 【答案】B
2. 【答案】B
3. 【答案】C
4. 【答案】B
5. 【答案】D
【解析】 一次函数 中,,
直线从左往右下降,
又 常数项 ,
直线与 轴交于负半轴,
直线经过第二、三、四象限.
故选:D.
6. 【答案】C
7. 【答案】B
【解析】观察函数图象可知:当 时,直线 在直线 的上方,
不等式 的解集为 .
8. 【答案】A
9. 【答案】D
10. 【答案】D
【解析】由题意可知:当 在 上时,这时构不成三角形,此时 ,
当 在 上时, 的面积在增大, 与 重合时最大为 ,此时 ;
当 在 上时, 的面积不变等于 ,此时 ;
当 在 上时, 的面积在减小,此时 .
11. 【答案】A
【解析】由题意 ,,,
,
取点 ,连接 ,,.
,
,
,
,,
,
,
,,
,
,
,
,
的最小值为线段 的长,
当 ,, 共线时, 的值最小,
直线 的解析式为:,
,
当 的值最小时,则 点的坐标为 .
12. 【答案】B
【解析】 在直线 中,
令 ,则有 ,
,
,
令 ,则有 ,
,故①正确;
点 , 关于 轴对称,
,
,
设直线 的解析式为 ,
,
,
直线 的解析式为 ,故②错误;
由①知,,
,
,
,
,
由题意知,,,,
,
,故③正确;
④由③知:,
在 中,令 ,,
,
.
④错误.
综上所述,正确的结论有 个.
二、填空题(共7题)
13. 【答案】
14. 【答案】
【解析】 的函数值 随 的增大而增大,
,解得 .
15. 【答案】
【解析】【分析】观察函数的图象与相交于点,,从而求解;
【解析】解:观察图象可知,与相交于点,,
可求出方方程组的解为,
故答案为:
【点评】此题主要考查一次函数与二元一次方程组,关键是能根据函数图象的交点解方程组.
16. 【答案】
【解析】 一次函数 中,,
随 的增大而减小.
,
.
17. 【答案】
【解析】当 时,,,
由图象得:不等式 的解集为:.
18. 【答案】三
【解析】 有解,
,,.
,
,
过二、四象限.
又 ,
过一、二象限,
不过三象限.
19. 【答案】
【解析】作 垂直直线 于点 .
易知 为等腰直角三角形,,.
作 轴于点 ,可得 .
当线段 最短时,点 的坐标为 , 为 .
三、解答题(共7题)
20. 【答案】
(1) ;
(2) 由图象得小明于 时(即下午 点)开始返回,
下午 点时距离保护区 千米,
下午 点到下午 点共 小时,
返回的速度为 (千米/时),
返回共需时间为 小时,
到家时间为 (时),
答:他下午 点才能到学校.
【解析】
(1) 小明乘车去时的平均速度是 千米/小时,
与 的关系式是 .
21. 【答案】
(1) 设直线 的解析表达式为 ,
把 代入得:
解得:
所以直线 的解析表达式为 .
(2) 解方程组:
得
则 ;
当 时,,
解得 ,
则 ,
所以 的面积 .
(3) 因为点 与点 到 的距离相等,
所以 点的纵坐标为 ,
当 时,,
解得 ,
所以 点坐标为 .
22. 【答案】
(1) 设每名熟练工和新工人每月分别可以安装 , 辆电动汽车,
根据题意,得解得答:每名熟练工和新工人每月分别可以安装 , 辆电动汽车;
(2) 设工厂有 名熟练工,
根据题意,得 ,,,
又 , 都是正整数,,
所以 .
即工厂有 种新工人的招聘方案.
① ,,即新工人 人,熟练工 人;
② ,,即新工人 人,熟练工 人;
③ ,,即新工人 人,熟练工 人;
④ ,,即新工人 人,熟练工 人;
(3) 结合()知:要使新工人的数量多于熟练工,则 ,;或 ,;或 ,,
根据题意,得 ,
要使工厂每月支出的工资总额 (元)尽可能地少,则 应最大,
显然当 , 时,(即新工人 人,熟练工 人),工厂每月支出的工资总额 (元)尽可能地少.
23. 【答案】
(1)
(2) ,
即 .
在一次函数 中,
因为 ,且 ,
所以当 时,(元).
即当甲仓库运往A果园 吨有机化肥时,总运费最省,是 元.
24. 【答案】
(1) 把 代入一次函数 ,可得
,
解得 ,
,
设 的解析式为 ,则 ,
解得 ,
的解析式为 .
(2) 如图,
过 作 于 , 于 ,则 ,,
,令 ,则 ;令 ,则 ,
,,
,,
.
(3) 或 或 .
【解析】
(3) 一次函数 的图象为 ,且 ,, 不能围成三角形,
当 经过点 时,;
当 , 平行时,;
当 , 平行时,;
故 的值为 或 或 .
25. 【答案】
(1) ① ,
②
③轴对称;旋转
(2) .
(3) 如图①.
(4) .
【解析】
(4) 在 中,由等积法得 ,
,
当点 移到点 时 ,
此时 ,
.
26. 【答案】
(1) 方程组 的解为:
,
,,
点 的坐标为:,
过 作 轴于 ,如图 所示:
且 ,
是等腰直角三角形,
,
点 的坐标为 .
(2) ①过点 作 轴于 ,如图 所示:
时,直线 恰好过点 ,
,,
点 的坐标为 ,
设直线 的解析式为:,
把 代入得:,
,
直线 的解析式为:,
,
设直线 的解析式为:,
把 代入得:,
,
直线 的解析式为:,
,
当 时,
,即 .
,,.
设直线 的解析式为 ,
将 代入得 解得
直线 的解析式为 .
设直线 的解析式为 ,
将 代入得 解得
直线 的解析式为 .
当 , 在 上,, 在 上,.
.
当 时, 在 上 , 在 上,,
.
.
②将 代入 ,解得 , 成立,
将 代入 ,解得 ,,不成立,
将 代入 ,解得 ,,成立.
综上所述,满足条件的点 的横坐标 的值为 或 .
一、选择题(共12题)
下列说法正确的是
A.过原点的直线都是正比例函数 B.正比例函数图象经过原点
C. 是正比例函数 D. 是正比例函数
下列函数中,是一次函数的有
();();();();().
A. 个 B. 个 C. 个 D. 个
当 时,一次函数 的图象不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
对于函数 ,下列结论正确的是
A.它的图象必经过点 B.它的图象经过第一、二、四象限
C.当 时, D. 的值随 值的增大而增大
一次函数 的图象大致是
A. B. C. D.
如图,直线 与 轴、 轴分别交于点 和点 ,点 , 分别为线段 , 的中点,点 为 上一动点,当 最小时,点 的坐标为
A. B. C. D.
(2018·金华市东阳市·期末)如图,经过点 的直线 与直线 相交于点 ,则不等式 的解集为
A. B. C. D.
如图,在平面直角坐标系中,函数 和 的图象分别为直线 ,,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 , 依次进行下去,则点 的坐标为
A. B.
C. D.
如图,直线 与 轴、 轴分别交于 , 两点,点 是 上一点,若直线 沿 折叠,点 恰好落在 轴上的点 处,则点 的坐标是
A. B. C. D.
如图,正方形 的边长为 ,点 为正方形边上一动点,若点 从点 出发沿 匀速运动一周.设点 走过的路程为 , 的面积为 ,则下列图象能大致反映 与 的函数关系的是
A. B. C. D.
如图,已知直线 : 分别交 轴、 轴于点 , 两点,,, 分别为线段 和线段 上一动点, 交 轴于点 ,且 .当 的值最小时,则 点的坐标为
A. B. C. D.
如图,直角坐标系 中,,直线 与 轴交于点 ,直线 与 轴及直线 分别交于点 ,,点 , 关于 轴对称,连接 ,下列结论正确的个数是
① ,;
②直线 的解析式为:;
③面积的和 ,则 ;
④设直线 与 轴相交于点 ,则 .
A. 个 B. 个 C. 个 D. 个
二、填空题(共7题)
将直线 向下平移 个单位,所得直线的函数表达式是 .
在一次函数 中, 随 的增大而增大,则 的取值范围是 .
如图,利用函数图象可知方程组的解为 .
一次函数 的图象上有两点 和 ,且 ,则 与 的大小关系为 .
如图,在平面直角坐标系中,函数 与 的图象交于点 ,则不等式 的解集为 .
关于 的一元一次不等式组 有解,则直线 不经过第 象限.
如图,点 的坐标为 ,点 在直线 上运动,连接 ,则线段 的长的最小值为 .
三、解答题(共7题)
早晨 点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离 (千米)与他离校的时间 (小时)之间的图象.根据图象,完成下面问题:
(1) 小明乘车去保护区的速度是 千米/小时,线段 所表示的 与 的关系式是 ;
(2) 已知下午 点时,小明距保护区 千米,问他何时才能回到学校?
如图,直线 的解析表达式为 ,且 与 轴交于点 ,直线 经过点 ,,直线 和 交于点 .
(1) 求直线 的解析表达式.
(2) 求 的面积.
(3) 直线 上存在异于点 的另一点 ,使 与 面积相等,求出点 的坐标.
面对资源紧缺与环境保护问题,发展电动汽车成为汽车工业发展的主流趋势.我国某著名汽车制造厂开发了一款新式电动汽车,计划一年生产安装 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现: 名熟练工和 名新工人每月可安装 辆电动汽车; 名熟练工和 名新工人每月可安装 辆电动汽车.
(1) 每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2) 如果工厂招聘 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3) 在()的条件下,工厂给安装电动汽车的每名熟练工每月发 元的工资,给每名新工人每月发 元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额 (元)尽可能的少?
“绿水青山就是金山银山”.为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥.甲、乙两个仓库分别可运出 吨和 吨有机化肥;A,B两个果园分别需用 吨和 吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
设甲仓库运往A果园 吨有机化肥,若汽车每吨每千米的运费为 元.
(1) 根据题意,填写下表.
(2) 设总运费为 元,求 关于 的函数表达式,并求出当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
如图,直角坐标系 中,一次函数 的图象 分别与 , 轴交于 , 两点,正比例函数的图象 与 交于点 .
(1) 求 的值及 的解析式.
(2) 求 的值.
(3) 一次函数 的图象为 ,且 ,, 不能围成三角形,直接写出 的值.
在平面直角坐标系中,点 的坐标为 ,点 的变换点 的坐标定义如下:当 时,点 的坐标为 ,当 时,点 的坐标为 .
(1) ①求 的变换点坐标 .
②若点 的变换点为 ,连接 ,,则 .
③由上面二个问题的解决,请思考:
当点 的变换点为 时,点 与 是 变换.
当点 的变换点为 时,点 与 是 变换.(选填“轴对称”或“旋转”或“中心对称”或“平移”)
(2) 直线 上所有点的变换点组成一个新图形记为 ,请求出 的解析式.
(3) 如图①,直线 上所有点的变换点组成一个新图形记为 ,请在图①中画出图形 .
(4) 点 在直线 上,点 是点 的变换点,连接 ,直接写出 的取值范围.
如图,在坐标系中,四边形 的顶点 是坐标原点,点 在第一象限,点 在第四象限、点 在 轴的正半轴上. 且 ,, 的长分别是二元一次方程组 的解 .
(1) 求点 和点 的坐标.
(2) 点 是线段 上的动点(点 不与点 , 重合),过点 的直线 与 轴平行,直线 交边 或边 点 ,交边 或边 于点 .设点 的横坐标为 ,线段 的长度为 .已知 时,直线 恰好过点 .
①求 关于 的函数关系式.
②当 时,求点 的横坐标 的值.
答案
一、选择题(共12题)
1. 【答案】B
2. 【答案】B
3. 【答案】C
4. 【答案】B
5. 【答案】D
【解析】 一次函数 中,,
直线从左往右下降,
又 常数项 ,
直线与 轴交于负半轴,
直线经过第二、三、四象限.
故选:D.
6. 【答案】C
7. 【答案】B
【解析】观察函数图象可知:当 时,直线 在直线 的上方,
不等式 的解集为 .
8. 【答案】A
9. 【答案】D
10. 【答案】D
【解析】由题意可知:当 在 上时,这时构不成三角形,此时 ,
当 在 上时, 的面积在增大, 与 重合时最大为 ,此时 ;
当 在 上时, 的面积不变等于 ,此时 ;
当 在 上时, 的面积在减小,此时 .
11. 【答案】A
【解析】由题意 ,,,
,
取点 ,连接 ,,.
,
,
,
,,
,
,
,,
,
,
,
,
的最小值为线段 的长,
当 ,, 共线时, 的值最小,
直线 的解析式为:,
,
当 的值最小时,则 点的坐标为 .
12. 【答案】B
【解析】 在直线 中,
令 ,则有 ,
,
,
令 ,则有 ,
,故①正确;
点 , 关于 轴对称,
,
,
设直线 的解析式为 ,
,
,
直线 的解析式为 ,故②错误;
由①知,,
,
,
,
,
由题意知,,,,
,
,故③正确;
④由③知:,
在 中,令 ,,
,
.
④错误.
综上所述,正确的结论有 个.
二、填空题(共7题)
13. 【答案】
14. 【答案】
【解析】 的函数值 随 的增大而增大,
,解得 .
15. 【答案】
【解析】【分析】观察函数的图象与相交于点,,从而求解;
【解析】解:观察图象可知,与相交于点,,
可求出方方程组的解为,
故答案为:
【点评】此题主要考查一次函数与二元一次方程组,关键是能根据函数图象的交点解方程组.
16. 【答案】
【解析】 一次函数 中,,
随 的增大而减小.
,
.
17. 【答案】
【解析】当 时,,,
由图象得:不等式 的解集为:.
18. 【答案】三
【解析】 有解,
,,.
,
,
过二、四象限.
又 ,
过一、二象限,
不过三象限.
19. 【答案】
【解析】作 垂直直线 于点 .
易知 为等腰直角三角形,,.
作 轴于点 ,可得 .
当线段 最短时,点 的坐标为 , 为 .
三、解答题(共7题)
20. 【答案】
(1) ;
(2) 由图象得小明于 时(即下午 点)开始返回,
下午 点时距离保护区 千米,
下午 点到下午 点共 小时,
返回的速度为 (千米/时),
返回共需时间为 小时,
到家时间为 (时),
答:他下午 点才能到学校.
【解析】
(1) 小明乘车去时的平均速度是 千米/小时,
与 的关系式是 .
21. 【答案】
(1) 设直线 的解析表达式为 ,
把 代入得:
解得:
所以直线 的解析表达式为 .
(2) 解方程组:
得
则 ;
当 时,,
解得 ,
则 ,
所以 的面积 .
(3) 因为点 与点 到 的距离相等,
所以 点的纵坐标为 ,
当 时,,
解得 ,
所以 点坐标为 .
22. 【答案】
(1) 设每名熟练工和新工人每月分别可以安装 , 辆电动汽车,
根据题意,得解得答:每名熟练工和新工人每月分别可以安装 , 辆电动汽车;
(2) 设工厂有 名熟练工,
根据题意,得 ,,,
又 , 都是正整数,,
所以 .
即工厂有 种新工人的招聘方案.
① ,,即新工人 人,熟练工 人;
② ,,即新工人 人,熟练工 人;
③ ,,即新工人 人,熟练工 人;
④ ,,即新工人 人,熟练工 人;
(3) 结合()知:要使新工人的数量多于熟练工,则 ,;或 ,;或 ,,
根据题意,得 ,
要使工厂每月支出的工资总额 (元)尽可能地少,则 应最大,
显然当 , 时,(即新工人 人,熟练工 人),工厂每月支出的工资总额 (元)尽可能地少.
23. 【答案】
(1)
(2) ,
即 .
在一次函数 中,
因为 ,且 ,
所以当 时,(元).
即当甲仓库运往A果园 吨有机化肥时,总运费最省,是 元.
24. 【答案】
(1) 把 代入一次函数 ,可得
,
解得 ,
,
设 的解析式为 ,则 ,
解得 ,
的解析式为 .
(2) 如图,
过 作 于 , 于 ,则 ,,
,令 ,则 ;令 ,则 ,
,,
,,
.
(3) 或 或 .
【解析】
(3) 一次函数 的图象为 ,且 ,, 不能围成三角形,
当 经过点 时,;
当 , 平行时,;
当 , 平行时,;
故 的值为 或 或 .
25. 【答案】
(1) ① ,
②
③轴对称;旋转
(2) .
(3) 如图①.
(4) .
【解析】
(4) 在 中,由等积法得 ,
,
当点 移到点 时 ,
此时 ,
.
26. 【答案】
(1) 方程组 的解为:
,
,,
点 的坐标为:,
过 作 轴于 ,如图 所示:
且 ,
是等腰直角三角形,
,
点 的坐标为 .
(2) ①过点 作 轴于 ,如图 所示:
时,直线 恰好过点 ,
,,
点 的坐标为 ,
设直线 的解析式为:,
把 代入得:,
,
直线 的解析式为:,
,
设直线 的解析式为:,
把 代入得:,
,
直线 的解析式为:,
,
当 时,
,即 .
,,.
设直线 的解析式为 ,
将 代入得 解得
直线 的解析式为 .
设直线 的解析式为 ,
将 代入得 解得
直线 的解析式为 .
当 , 在 上,, 在 上,.
.
当 时, 在 上 , 在 上,,
.
.
②将 代入 ,解得 , 成立,
将 代入 ,解得 ,,不成立,
将 代入 ,解得 ,,成立.
综上所述,满足条件的点 的横坐标 的值为 或 .
