1.2.2 直角三角形 课件(共19张PPT)2022-2023学年北师大版八年级数学下册
文档属性
| 名称 | 1.2.2 直角三角形 课件(共19张PPT)2022-2023学年北师大版八年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 353.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 14:46:47 | ||
图片预览





文档简介
(共19张PPT)
北师大版数学 八年级下册
第一章 三角形的证明
教学课件
2. 直角三角形
第2课时
教学目标——重点难点
第一章 三角形的证明
1.理解并掌握证明直角三角形全等的“斜边直角边定理”.(重点)
2.综合利用直角三角形的性质及直角三角形全等的判定解决问题.(重点)
教学目标——温故知新
第一章 三角形的证明
知识储备
1.尺规作图中直尺和圆规的作用分别是什么?
直尺:几何作图中,没有刻度的直尺只能用来连接两点间的线段、画直线、射线等. 由于没有刻度,所以不能用来度量线段的长度.
圆规:几何作图中,圆规只能用来截取线段或画圆弧.
2.判定两个三角形全等的方法有哪些?这些判定方法适用于直角三角形吗?
SSS、ASA、SAS、AAS
因为直角三角形是特殊的三角形,所以一般三角形全等的判定方法都适用于直角三角形.
教学过程——新课引入
第一章 三角形的证明
议一议
我们学习了利用尺规作图作一条线段等于已知线段,作一个角等于已知角,如果已知一个直角,两条线段,你能以这两条线段中较短的一条线段为直角边,较长的一条线段为斜边作一个直角三角形吗?
α
教学过程——新知探究
第一章 三角形的证明
知识点1 利用直尺和圆规作直角三角形
作已知直角边和斜边的直角三角形
以课本19页已知线段、 和∠α为已知条件,按照课本的作法,作一个直角三角形. 作完后和同桌作的直角三角形比较,你们作的直角三角形全等吗?
α
教学过程——新知探究
第一章 三角形的证明
知识点1 利用直尺和圆规作直角三角形
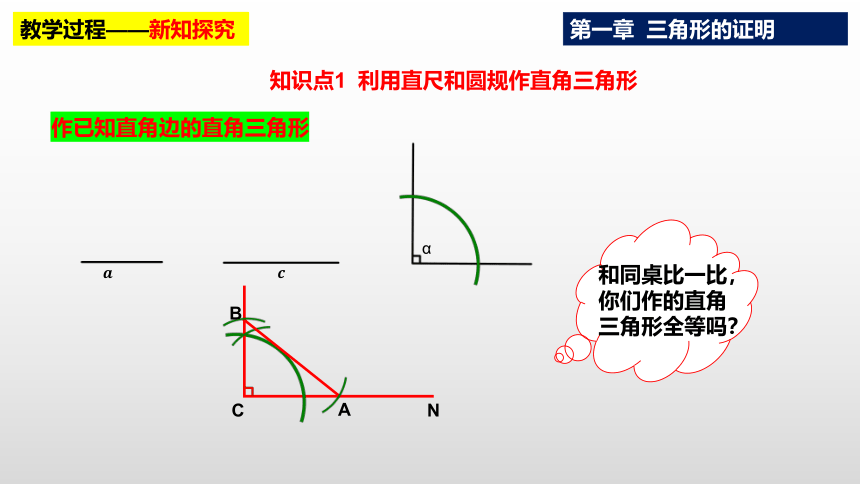
作已知直角边的直角三角形
C
N
B
A
和同桌比一比,你们作的直角三角形全等吗?
教学过程——新知探究
第一章 三角形的证明
知识点2 直角三角形全等的判定
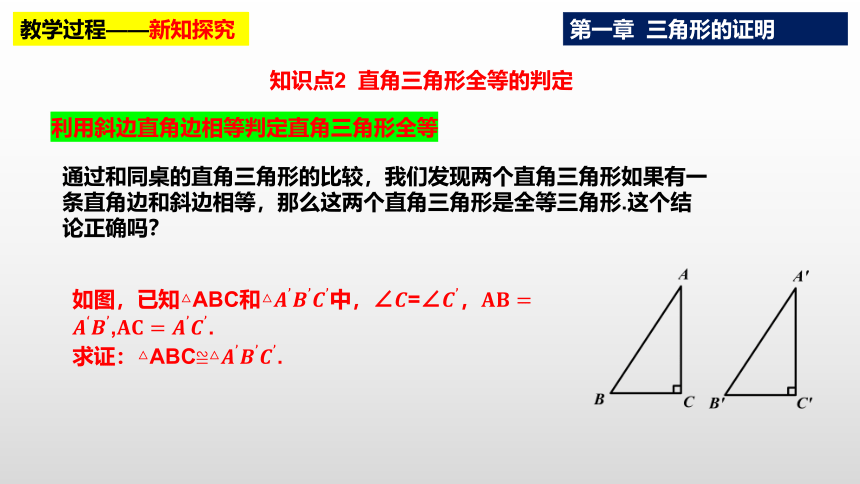
利用斜边直角边相等判定直角三角形全等
通过和同桌的直角三角形的比较,我们发现两个直角三角形如果有一条直角边和斜边相等,那么这两个直角三角形是全等三角形.这个结论正确吗?
如图,已知△ABC和△中,∠=∠,,.
求证:△ABC≌△.
教学过程——新知探究
第一章 三角形的证明
知识点2 直角三角形全等的判定
利用斜边直角边相等判定直角三角形全等
证明:在△ABC中,
∵,
∴(勾股定理).
同理,.
∴ .
∴≌△(SSS).
∵,
教学过程——新知探究
第一章 三角形的证明
知识点2 直角三角形全等的判定
利用斜边直角边相等判定直角三角形全等
通过上面的证明,我们得到判定直角三角形全等的一种新方法:
定理 斜边和一条直角边分别相等的两个直角三角形全等(简称为“斜边、直角边”或“HL”).
符号语言:如图,在已知Rt△ABC和Rt△中,
∵∠∠
,
∴ ≌ △(HL).
教学过程——新知探究
第一章 三角形的证明
回顾课本
读一读
认真阅读课本第20页例题,体会直角三角形的全等的判定定理在解题中应用.
教学过程——新知探究
第一章 三角形的证明
做一做
学以致用
如图,已知∠AOB,你能只用一把三角尺(三角尺不能用于测量)和铅笔画出∠AOB的角平分线吗?
实际做一做,再证明.
教学过程——典例精析
第一章 三角形的证明
听一听
例1 在如图所示的三角形纸片ABC中,∠C=90°,∠B=30°.按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕):①折叠三角形纸片ABC,使点B与点A重合;②将折叠后的纸片再沿AD折叠.
(1)由步骤①可以得到哪些等量关系?
(2)请证明△ACD≌△AED;
(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形?
教学过程——典例精析
第一章 三角形的证明
听一听
解:(1)由步骤①可以得△ADE≌△BDE、∠AED=∠BED=90°、AE=AB...
(2)证明:在△中,使∠90°,∠B=30°,
∴AC=AB.
∵AE=AB
∴AC=AE.
∵∠C=∠AED=90°,AD=AD
∴ ≌ △(HL)
(3)按照这种方法不能将任意一个直角三角形分成三个全等的小三角形.
教学过程——典例精析
第一章 三角形的证明
听一听
例2 已知:如图,在△ABC中,∠B=90°,过顶点C作CD//AB,连接AD,作CE⊥AD于E,且CE=CB,.求证:∠CDE=2∠BAC.
教学过程——典例精析
第一章 三角形的证明
听一听
解:∵CE⊥AD
∴∠AEC=90°.
又∵∠B=90°,CE=CD,AC=AC,
∴ ≌ △(HL)
∴ (全等三角形的对应角相等).
∵CD//AB
∴ (两直线平行,内错角相等).
∴.
∵∠CDE=∠EAD+∠ACD=2∠ACD,
∴.
教学过程——随堂练习
第一章 三角形的证明
做一做
课本第20页“随堂练习”.
教学过程——课堂小结
第一章 三角形的证明
记一记
本节课学习了直角三角形全等的判定.
定理 斜边和一条直角边分别相等的两个直角三角形全等(简称为“斜边、直角边”或“HL”).
符号语言:如图,在已知Rt△ABC和Rt△中,
∵∠∠=90°
,
∴ ≌ △(HL).
课后巩固——分层作业
第一章 三角形的证明
练一练
完成相关作业
结束新课
感谢聆听
第一章 三角形的证明
北师大版数学 八年级下册
第一章 三角形的证明
教学课件
2. 直角三角形
第2课时
教学目标——重点难点
第一章 三角形的证明
1.理解并掌握证明直角三角形全等的“斜边直角边定理”.(重点)
2.综合利用直角三角形的性质及直角三角形全等的判定解决问题.(重点)
教学目标——温故知新
第一章 三角形的证明
知识储备
1.尺规作图中直尺和圆规的作用分别是什么?
直尺:几何作图中,没有刻度的直尺只能用来连接两点间的线段、画直线、射线等. 由于没有刻度,所以不能用来度量线段的长度.
圆规:几何作图中,圆规只能用来截取线段或画圆弧.
2.判定两个三角形全等的方法有哪些?这些判定方法适用于直角三角形吗?
SSS、ASA、SAS、AAS
因为直角三角形是特殊的三角形,所以一般三角形全等的判定方法都适用于直角三角形.
教学过程——新课引入
第一章 三角形的证明
议一议
我们学习了利用尺规作图作一条线段等于已知线段,作一个角等于已知角,如果已知一个直角,两条线段,你能以这两条线段中较短的一条线段为直角边,较长的一条线段为斜边作一个直角三角形吗?
α
教学过程——新知探究
第一章 三角形的证明
知识点1 利用直尺和圆规作直角三角形
作已知直角边和斜边的直角三角形
以课本19页已知线段、 和∠α为已知条件,按照课本的作法,作一个直角三角形. 作完后和同桌作的直角三角形比较,你们作的直角三角形全等吗?
α
教学过程——新知探究
第一章 三角形的证明
知识点1 利用直尺和圆规作直角三角形
作已知直角边的直角三角形
C
N
B
A
和同桌比一比,你们作的直角三角形全等吗?
教学过程——新知探究
第一章 三角形的证明
知识点2 直角三角形全等的判定
利用斜边直角边相等判定直角三角形全等
通过和同桌的直角三角形的比较,我们发现两个直角三角形如果有一条直角边和斜边相等,那么这两个直角三角形是全等三角形.这个结论正确吗?
如图,已知△ABC和△中,∠=∠,,.
求证:△ABC≌△.
教学过程——新知探究
第一章 三角形的证明
知识点2 直角三角形全等的判定
利用斜边直角边相等判定直角三角形全等
证明:在△ABC中,
∵,
∴(勾股定理).
同理,.
∴ .
∴≌△(SSS).
∵,
教学过程——新知探究
第一章 三角形的证明
知识点2 直角三角形全等的判定
利用斜边直角边相等判定直角三角形全等
通过上面的证明,我们得到判定直角三角形全等的一种新方法:
定理 斜边和一条直角边分别相等的两个直角三角形全等(简称为“斜边、直角边”或“HL”).
符号语言:如图,在已知Rt△ABC和Rt△中,
∵∠∠
,
∴ ≌ △(HL).
教学过程——新知探究
第一章 三角形的证明
回顾课本
读一读
认真阅读课本第20页例题,体会直角三角形的全等的判定定理在解题中应用.
教学过程——新知探究
第一章 三角形的证明
做一做
学以致用
如图,已知∠AOB,你能只用一把三角尺(三角尺不能用于测量)和铅笔画出∠AOB的角平分线吗?
实际做一做,再证明.
教学过程——典例精析
第一章 三角形的证明
听一听
例1 在如图所示的三角形纸片ABC中,∠C=90°,∠B=30°.按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕):①折叠三角形纸片ABC,使点B与点A重合;②将折叠后的纸片再沿AD折叠.
(1)由步骤①可以得到哪些等量关系?
(2)请证明△ACD≌△AED;
(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形?
教学过程——典例精析
第一章 三角形的证明
听一听
解:(1)由步骤①可以得△ADE≌△BDE、∠AED=∠BED=90°、AE=AB...
(2)证明:在△中,使∠90°,∠B=30°,
∴AC=AB.
∵AE=AB
∴AC=AE.
∵∠C=∠AED=90°,AD=AD
∴ ≌ △(HL)
(3)按照这种方法不能将任意一个直角三角形分成三个全等的小三角形.
教学过程——典例精析
第一章 三角形的证明
听一听
例2 已知:如图,在△ABC中,∠B=90°,过顶点C作CD//AB,连接AD,作CE⊥AD于E,且CE=CB,.求证:∠CDE=2∠BAC.
教学过程——典例精析
第一章 三角形的证明
听一听
解:∵CE⊥AD
∴∠AEC=90°.
又∵∠B=90°,CE=CD,AC=AC,
∴ ≌ △(HL)
∴ (全等三角形的对应角相等).
∵CD//AB
∴ (两直线平行,内错角相等).
∴.
∵∠CDE=∠EAD+∠ACD=2∠ACD,
∴.
教学过程——随堂练习
第一章 三角形的证明
做一做
课本第20页“随堂练习”.
教学过程——课堂小结
第一章 三角形的证明
记一记
本节课学习了直角三角形全等的判定.
定理 斜边和一条直角边分别相等的两个直角三角形全等(简称为“斜边、直角边”或“HL”).
符号语言:如图,在已知Rt△ABC和Rt△中,
∵∠∠=90°
,
∴ ≌ △(HL).
课后巩固——分层作业
第一章 三角形的证明
练一练
完成相关作业
结束新课
感谢聆听
第一章 三角形的证明
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
