3.1.2图形的平移 课件(共15张PPT)2022—2023学年北师大版数学八年级下册
文档属性
| 名称 | 3.1.2图形的平移 课件(共15张PPT)2022—2023学年北师大版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-05 16:07:59 | ||
图片预览






文档简介
(共15张PPT)
第三章 图形的平移
与旋转
第1节 图形的平移(第2课时)
北师大版 八年级下册
学习重点
学习难点
在具体情境中感受平面直角坐标系中点的坐标变化与图形的平移之间的内在关系.
能准确地概括出图形的变化与坐标变化的一般规律.
学习目标
1.在平面直角坐标系网格纸上探究已知顶点坐标的多边形(变化的鱼)横向(或纵向)平移一次,
其对应顶点坐标变化的规律,认识图形变换与坐标之间的内在联系.
2.在画图活动过程中,提高学生的动手能力.
3.经历图形平移的观察、操作、分析、概括等过程,进一步积累数学活动经验.
前 言
创设情境,导入新课
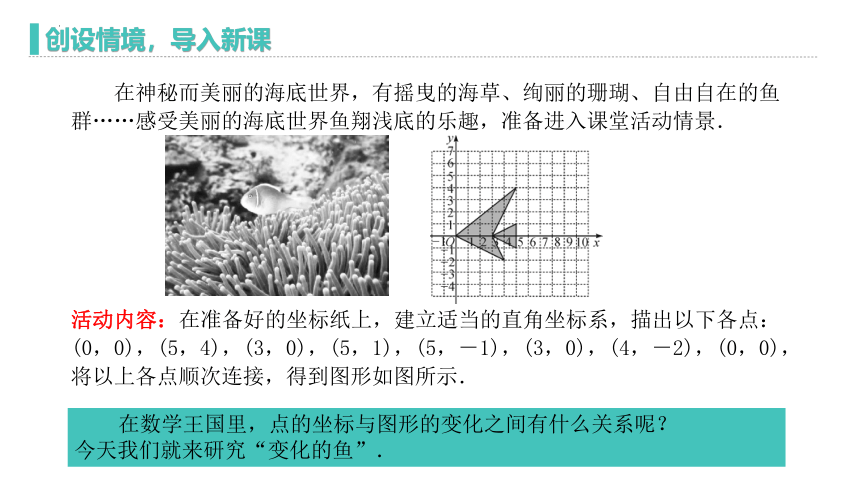
在神秘而美丽的海底世界,有摇曳的海草、绚丽的珊瑚、自由自在的鱼群……感受美丽的海底世界鱼翔浅底的乐趣,准备进入课堂活动情景.
活动内容:在准备好的坐标纸上,建立适当的直角坐标系,描出以下各点:
(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),将以上各点顺次连接,得到图形如图所示.
在数学王国里,点的坐标与图形的变化之间有什么关系呢?
今天我们就来研究“变化的鱼”.
实践探究,交流新知
探究1 探究图形平移后,各点坐标的变化规律
如图,图中的“鱼”是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)的点用线段依次连接而成的.将这条“鱼”向右平移5个单位长度.
(1)画出平移后的新“鱼”;
(2)写出新“鱼”对应各点的坐标;
(3)你发现对应点的坐标之间有什么关系?
解:
(1)
(2)新“鱼”对应各点的坐标.
(5,0),(10,4),(8,0),(10,1),
(10,-1),(8,0),(9,-2),(5,0).
纵坐标不变,横坐标都加5
实践探究,交流新知
探究1 探究图形平移后,各点坐标的变化规律
如果将原来的“鱼”向左平移4个单位长度呢?请你先想一想,然后再具体做一做.
纵坐标不变,横坐标都减4
想一想:如果将图中的“鱼”向上平移3个单位长度,那么平移前后的两条“鱼”中,对应点的坐标之间有什么关系?如果将图中的“鱼”向下平移2个单位长度呢?
横坐标不变,纵坐标都加3
横坐标不变,纵坐标都减2
实践探究,交流新知
探究1 探究图形平移后,各点坐标的变化规律
根据以上的内容,如果平移的单位是常量a(a>0),原坐标为(x,y),你能写出图形平移后的对应点的坐标吗?
①原图形向右(向左)平移a个单位长度:对应点的坐标为(x±a,y)
②原图形向上(向下)平移a个单位长度:对应点的坐标为(x,y±a)
实践探究,交流新知
探究2 探究坐标变化后,图形的变化规律
如图,将图中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加3,再将得到的点用线段依次连接起来,从而画出一条新“鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?如果纵坐标保持不变,横坐标分别减2呢?
①纵坐标保持不变,横坐标分别加3:
原图形被向右平移3个单位长度.
②纵坐标保持不变,横坐标分别减2:
原图形被向左平移2个单位长度.
实践探究,交流新知
探究2 探究坐标变化后,图形的变化规律
将图中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加2,所得到的新“鱼”与原来的“鱼”相比又有什么变化?如果横坐标保持不变,纵坐标分别减2呢?
①横坐标保持不变,纵坐标分别加2,原图形被向上平移2个单位长度.
②横坐标保持不变,纵坐标分别减2,原图形被向下平移2个单位长度.
实践探究,交流新知
探究2 探究坐标变化后,图形的变化规律
根据以上的内容,如果坐标的变化是常量a(a>0),你能写出坐标变化后,图形的移动规律吗?
①原图形各点的纵坐标保持不变,横坐标分别加(减)a:
图形向右(向左)平移a个单位长度.
②原图形各点的横坐标保持不变,纵坐标分别加(减)b:
图形向上(向下)平移a个单位长度.
开放训练,体现应用
例1 已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点
A′的坐标是( )
A.(6,1) B.(-2,1) C.(2,5) D.(2,-3)
例2 如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)点B关于y轴的对称点的坐标为 ;
(2)点A1的坐标为 .
D
(-3,2)
(-2,3)
开放训练,体现应用
变式训练
1.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,
那么平移后对应点A1的坐标是 .
2.如图,将四边形ABCD向左平移3个单位长度,那么点A的对应点
A′的坐标是( )
A.(6,2) B.(0,2)
C.(0,-1) D.(6,-1)
C
(1,3)
课堂检测,巩固新知
1. 如图,把笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇中点C的
坐标是(-1,1).若把此笑脸向右平移3个单位长度,则右眼B的坐标
是 .
2.如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),
把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是( )
A.(-2,3) B.(3,-1) C.(-3,1) D.(-5,2)
C
(3,3)
(第1题)
(第2题)
课堂检测,巩固新知
3. 如图,将△ABC向右平移2个单位长度,得到对应的△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标.
解:如图所示,
A1(0,5)
B1(-3,-2)
C1(4,3)
课堂小结,整体感知
1.课堂小结:
本节课学到了什么知识?
2.布置作业:
(1)教材第70页随堂练习第1,2题.
(2)教材第70页习题3.2第1,2,3,4题.
(1)探究图形平移后,各点坐标的变化规律
①原图形向右(向左)平移a个单位长度:对应点的坐标为(x±a,y).
②原图形向上(向下)平移a个单位长度:对应点的坐标为(x,y±a).
(2)探究坐标变化后,图形的变化规律
①原图形各点的纵坐标保持不变,横坐标分别加(减)a:
图形向右(向左)平移a个单位长度.
②原图形各点的横坐标保持不变,纵坐标分别加(减)b:
图形向上(向下)平移a个单位长度.
同学们,
下课!
第三章 图形的平移
与旋转
第1节 图形的平移(第2课时)
北师大版 八年级下册
学习重点
学习难点
在具体情境中感受平面直角坐标系中点的坐标变化与图形的平移之间的内在关系.
能准确地概括出图形的变化与坐标变化的一般规律.
学习目标
1.在平面直角坐标系网格纸上探究已知顶点坐标的多边形(变化的鱼)横向(或纵向)平移一次,
其对应顶点坐标变化的规律,认识图形变换与坐标之间的内在联系.
2.在画图活动过程中,提高学生的动手能力.
3.经历图形平移的观察、操作、分析、概括等过程,进一步积累数学活动经验.
前 言
创设情境,导入新课
在神秘而美丽的海底世界,有摇曳的海草、绚丽的珊瑚、自由自在的鱼群……感受美丽的海底世界鱼翔浅底的乐趣,准备进入课堂活动情景.
活动内容:在准备好的坐标纸上,建立适当的直角坐标系,描出以下各点:
(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),将以上各点顺次连接,得到图形如图所示.
在数学王国里,点的坐标与图形的变化之间有什么关系呢?
今天我们就来研究“变化的鱼”.
实践探究,交流新知
探究1 探究图形平移后,各点坐标的变化规律
如图,图中的“鱼”是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)的点用线段依次连接而成的.将这条“鱼”向右平移5个单位长度.
(1)画出平移后的新“鱼”;
(2)写出新“鱼”对应各点的坐标;
(3)你发现对应点的坐标之间有什么关系?
解:
(1)
(2)新“鱼”对应各点的坐标.
(5,0),(10,4),(8,0),(10,1),
(10,-1),(8,0),(9,-2),(5,0).
纵坐标不变,横坐标都加5
实践探究,交流新知
探究1 探究图形平移后,各点坐标的变化规律
如果将原来的“鱼”向左平移4个单位长度呢?请你先想一想,然后再具体做一做.
纵坐标不变,横坐标都减4
想一想:如果将图中的“鱼”向上平移3个单位长度,那么平移前后的两条“鱼”中,对应点的坐标之间有什么关系?如果将图中的“鱼”向下平移2个单位长度呢?
横坐标不变,纵坐标都加3
横坐标不变,纵坐标都减2
实践探究,交流新知
探究1 探究图形平移后,各点坐标的变化规律
根据以上的内容,如果平移的单位是常量a(a>0),原坐标为(x,y),你能写出图形平移后的对应点的坐标吗?
①原图形向右(向左)平移a个单位长度:对应点的坐标为(x±a,y)
②原图形向上(向下)平移a个单位长度:对应点的坐标为(x,y±a)
实践探究,交流新知
探究2 探究坐标变化后,图形的变化规律
如图,将图中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加3,再将得到的点用线段依次连接起来,从而画出一条新“鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?如果纵坐标保持不变,横坐标分别减2呢?
①纵坐标保持不变,横坐标分别加3:
原图形被向右平移3个单位长度.
②纵坐标保持不变,横坐标分别减2:
原图形被向左平移2个单位长度.
实践探究,交流新知
探究2 探究坐标变化后,图形的变化规律
将图中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加2,所得到的新“鱼”与原来的“鱼”相比又有什么变化?如果横坐标保持不变,纵坐标分别减2呢?
①横坐标保持不变,纵坐标分别加2,原图形被向上平移2个单位长度.
②横坐标保持不变,纵坐标分别减2,原图形被向下平移2个单位长度.
实践探究,交流新知
探究2 探究坐标变化后,图形的变化规律
根据以上的内容,如果坐标的变化是常量a(a>0),你能写出坐标变化后,图形的移动规律吗?
①原图形各点的纵坐标保持不变,横坐标分别加(减)a:
图形向右(向左)平移a个单位长度.
②原图形各点的横坐标保持不变,纵坐标分别加(减)b:
图形向上(向下)平移a个单位长度.
开放训练,体现应用
例1 已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点
A′的坐标是( )
A.(6,1) B.(-2,1) C.(2,5) D.(2,-3)
例2 如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)点B关于y轴的对称点的坐标为 ;
(2)点A1的坐标为 .
D
(-3,2)
(-2,3)
开放训练,体现应用
变式训练
1.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,
那么平移后对应点A1的坐标是 .
2.如图,将四边形ABCD向左平移3个单位长度,那么点A的对应点
A′的坐标是( )
A.(6,2) B.(0,2)
C.(0,-1) D.(6,-1)
C
(1,3)
课堂检测,巩固新知
1. 如图,把笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇中点C的
坐标是(-1,1).若把此笑脸向右平移3个单位长度,则右眼B的坐标
是 .
2.如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),
把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是( )
A.(-2,3) B.(3,-1) C.(-3,1) D.(-5,2)
C
(3,3)
(第1题)
(第2题)
课堂检测,巩固新知
3. 如图,将△ABC向右平移2个单位长度,得到对应的△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标.
解:如图所示,
A1(0,5)
B1(-3,-2)
C1(4,3)
课堂小结,整体感知
1.课堂小结:
本节课学到了什么知识?
2.布置作业:
(1)教材第70页随堂练习第1,2题.
(2)教材第70页习题3.2第1,2,3,4题.
(1)探究图形平移后,各点坐标的变化规律
①原图形向右(向左)平移a个单位长度:对应点的坐标为(x±a,y).
②原图形向上(向下)平移a个单位长度:对应点的坐标为(x,y±a).
(2)探究坐标变化后,图形的变化规律
①原图形各点的纵坐标保持不变,横坐标分别加(减)a:
图形向右(向左)平移a个单位长度.
②原图形各点的横坐标保持不变,纵坐标分别加(减)b:
图形向上(向下)平移a个单位长度.
同学们,
下课!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
